1 方框图分析法
方框图如下:
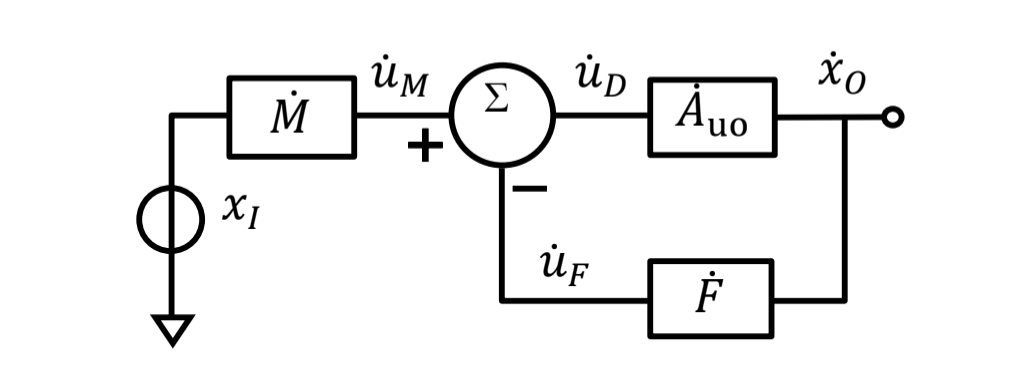
- 图中\(A_{uo}\)是一个电压输入的放大器的放大倍数,称为开环放大倍数。
- \(F\)为反馈系数,是一个矢量,是指输出信号\(x_{o}\)的多少倍回送到放大器的输入端。
- \(M\)为衰减系数,也是一个矢量,是指输入信号的多少倍,进入放大器的输入端。
根据上述三点,可列出输出信号的方程:\(x_{0}=(x_{I}M-x_{O}F)A_{uo}\)
并由此解得闭环放大倍数\(A_{uf}=\frac{x_{0}}{x_{I}}=\frac{M \times A_{uo}}{1+F \times A_{uo}}\)
又考虑到放大器的开环放大倍数\(A_{uo}\)趋于无穷大,因此可以近似得到闭环放大倍数\(A_{uf} \approx \frac{M}{F}\)
含义:当放大器的开环放大倍数与反馈系数的乘积足够大时,此时电路状态称为深度负反馈状态,且闭环放大倍数约为衰减系数和反馈系数的比值,与开环放大倍数无关。
2 衰减系数和反馈系数的求解方法
2.1 求衰减系数
将输出激励强制设为0,求解运放正输入端电压,并用输入激励表达:\(u_{+}|_{x_{O}=0}=g_{1}(x_{I})\)
将输出激励强制设为0,求解运放负输入端电压,并用输入激励表达:\(u_{-}|_{x_{O}=0}=g_{2}(x_{I})\)
然后就有:\(M=\frac{u_{+}|_{x_{O}=0}-u_{-}|_{x_{O}=0}}{x_{I}}=\frac{g_{1}(x_{I})-g_{2}(x_{I})}{x_{I}}\)
衰减系数的含义是指在不考虑输出回送的情况下,单纯的输入信号有多少加载到了运放输入端上
2.2 求反馈系数
将输入激励强制设为0,求解运放正输入端电压,并用输出激励表达:\(u_{+}|_{x_{I}=0}=g_{3}(x_{O})\)
将输入激励强制设为0,求解运放负输入端电压,并用输出激励表达:\(u_{-}|_{x_{I}=0}=g_{4}(x_{0})\)
然后就有:\(F=\frac{u_{-}|_{x_{I}=0}-u_{+}|_{x_{I}=0}}{x_{0}}=\frac{g_{4}(x_{O})-g_{3}(x_{0})}{x_{O}}\)
反馈系数的含义是指在不考虑输入的情况下,单纯的输出信号有多少加载到了运放的反相输入上
3 求解电路
求该电路的闭环放大倍数
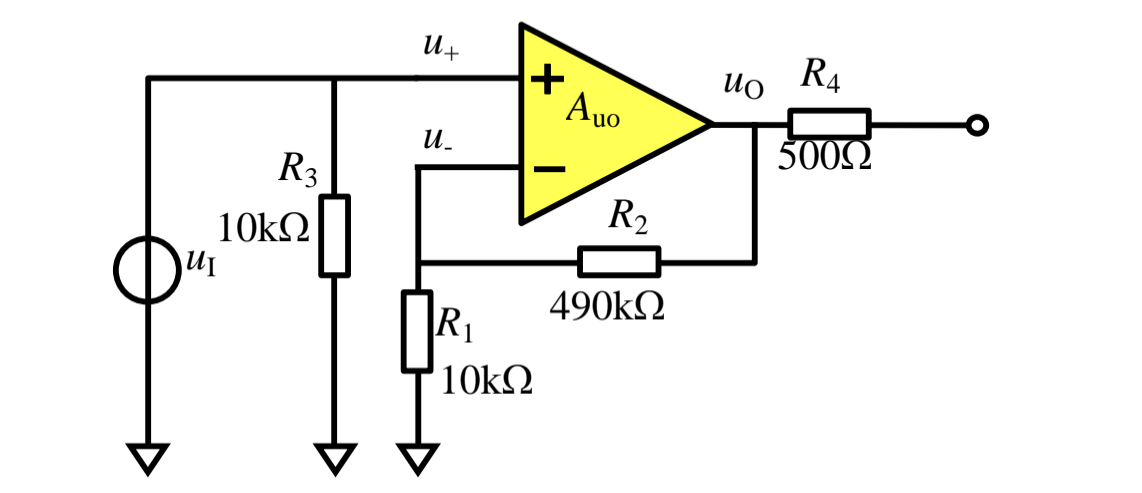
解:
先求衰减系数和反馈系数:
①将输出激励强制设为0,便有
正输入端电压:\(u_{+}|_{u_{o}=0}=u_{I}\),
负输入端电压:\(u_{-}|_{u_{o}=0}=0\),
所以衰减系数:\(M=\frac{u_{I}-0}{u_{I}}=1\)
②将输入激励强制设为0,便有
正输入端电压:\(u_{+}|_{u_{I}=0}=0\),
负输入端电压:\(u_{-}|_{u_{I}=0}=\frac{R_{1}}{R_{1}+R_{2}}\times U_{0}=\frac{1}{50}\times u_{0}\),
所以反馈系数:\(F=\frac{\frac{1}{50}\times u_{0}-0}{u_{O}}=\frac{1}{50}\)
综上可近似得到闭环放大倍数:\(A_{uf} \approx \frac{M}{F}=50\)