卷积的具体执行流程不属于本博客的重心。
问题描述
卷积的大致执行流程是卷积核对输入张量进行多项式求和运算。如果输入的张量有多个通道,如RGB三通道,那么卷积又是怎么执行的呢?1X1卷积(记作一维卷积)不能获取到局部特征,那么其存在的意义是什么呢?一维卷积的可学习参数是否就是1个呢?
问题总结:
- 多通道张量的卷积流程
- 一维卷积的作用
- 卷积的可学习参数。权重 = 可学习参数
多通道卷积
流程
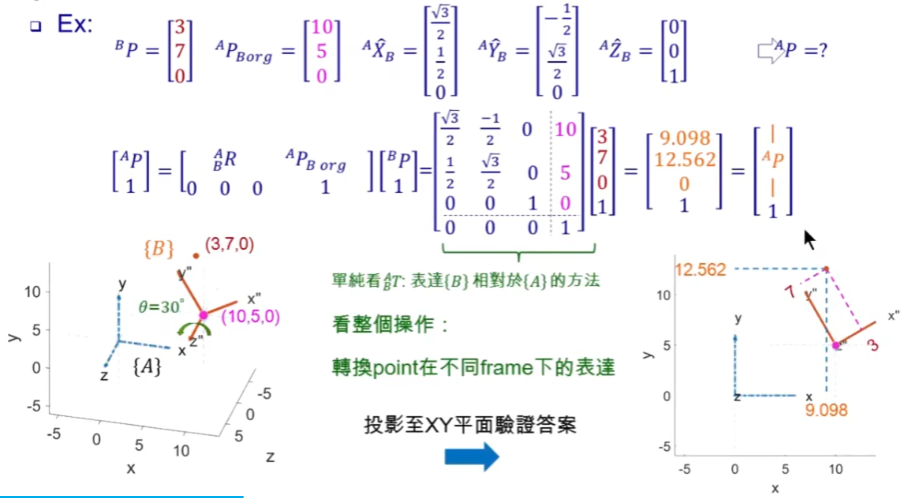
如图所示,假设输入的维度为(channels, height, weight) \(\rightarrow\) (3,3,3),卷积核的大小为(1, 1)。
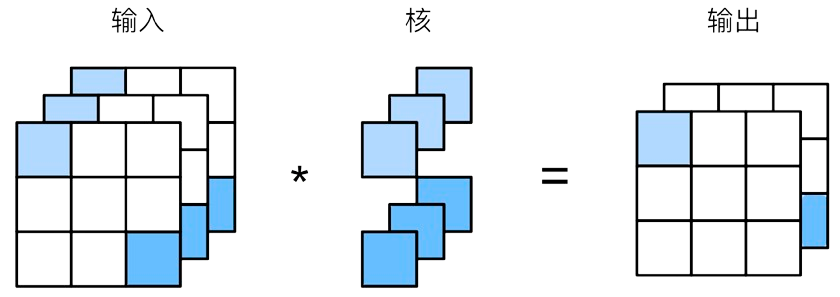
如果输入的维度只有1个通道,那么卷积核可以按照一般情况通过多项式求和的方式进行卷积。
但是如果输入是多维呢?同一个卷积核,对多个通道进行卷积,得到多个特征图,然后将各个特征图的各元素对应位置相加。从而得到一个输出特征图。正如图所示,中间的两个卷积核,“分裂”成三个(三个是对应输入数据的通道数)。一个卷积核 \(\rightarrow\) 一个输出特征图。
综上所示,可以简单理解为:
- 卷积核的批次大小(用批次batch形容其实不太准确)与输入的通道数相同
- 由多个通道卷积得到的多个特征图通过相加“聚合”为一个输出特征图
- 一个卷积核对应一个输出特征图
这也是为什么pytorch中使用卷积需要指明卷积的输入通道数和输出通道数。torch.nn.Conv2d(in_channels, out_channels, kernel_size)
启发
卷积可以改变输入数据的高、宽、通道数。
既然如此,卷积可以实现以下作用:
- 提升/降低通道数。提升通道数有利于提取到更深层次的特征。
- 一维卷积不能改变输入数据的高和宽,但是能改变通道数。因此,可以用一维卷积来模拟线性层(全连接层)。因为卷积的参数远小于线性层,所以可以一定程度上提高模型训练/推理速度。
卷积参数
首先,卷积中可学习的参数主要是卷积核内的参数。最开始卷积核内的参数是随机初始化的,通过梯度下降算法,不断对参数进行更新。但是卷积中可学习参数数量 \(\not=\) 卷积核中元素个数(\(height \times width\))
由多通道卷积流程可知,如果输入数据是多通道,那么在卷积的过程中,每个卷积核会“分裂”成通道数个,然后对每一个通道都进行卷积。所以,一个卷积核的参数量为$height \times width \times C_{in} \(。输出通道数量决定卷积核个数,所以**卷积层**的参数量为\)height \times width \times C_{in} \times C_{out}$。
事实上,每一个卷积核会给其输出特征图添加一个偏置(标量,可被更新)。
因此,最终卷积层参数量为: