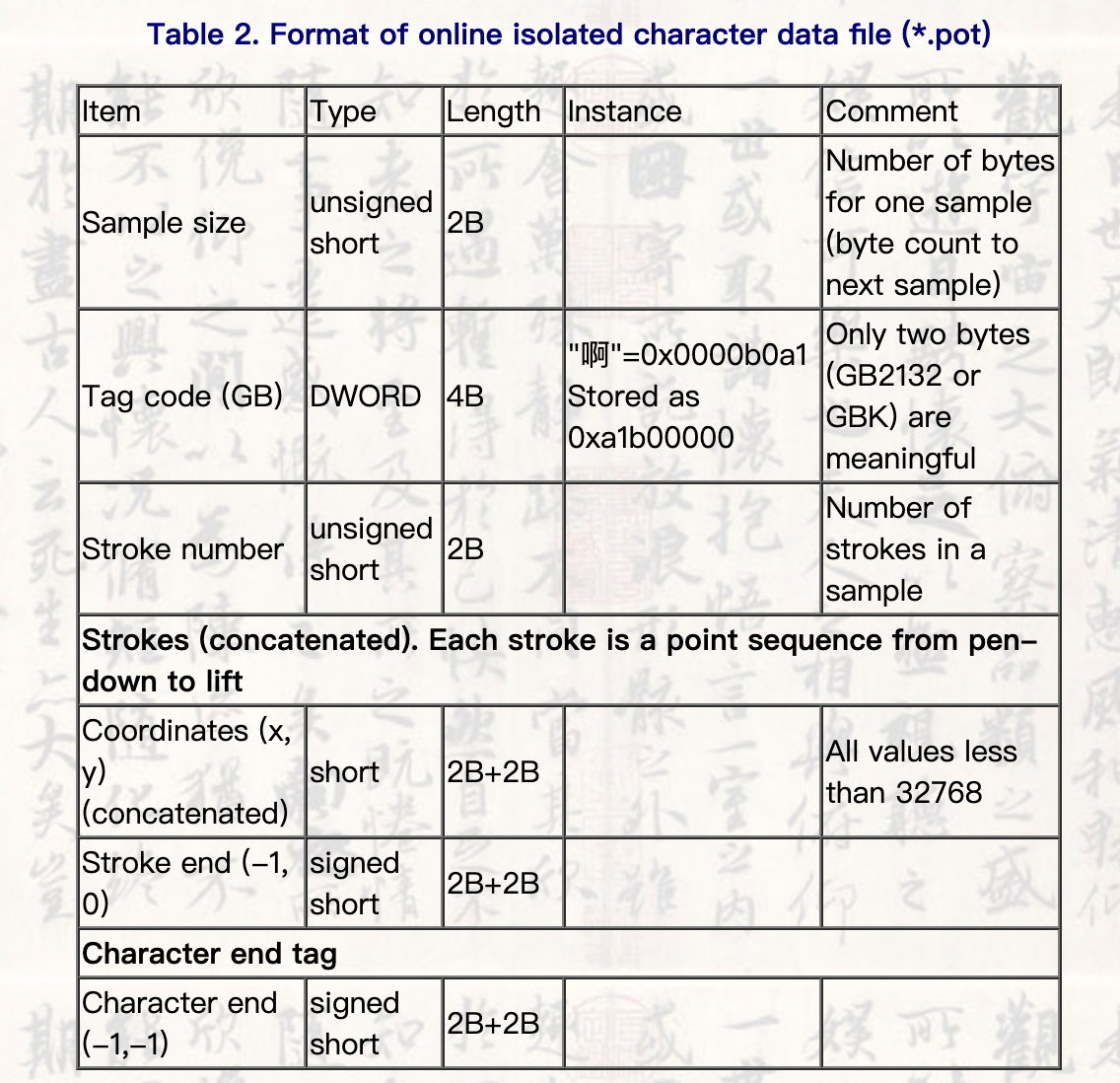
题意:
给出一个 \(n\) 个点的树,每个点有黑白两种颜色。初始时每个点都是黑色的。\(q\) 次操作,支持:
C x将第 \(x\) 个点的颜色反转。G询问树上两个黑色点的最远距离。
分析:
尝试使用点分树,对于一条路径,可以从点分树的 \(lca\) 处统计,由于涉及到删除和添加两种操作,因此可以用 multiset 来维护。
记 \(C_{i}\) 表示 \(i\) 的点分树子树内所有黑点到 \(i\) 的点分树父亲距离的可重集。因为需要保证每次的 \(C_{i}\) 都是不同子树,记 \(B_{i}\) 表示 \(i\) 的点分树儿子的 \(C_{j}\) 的可重集(特别的,如果 \(i\) 是黑色点,要把 \(0\) 也放进 \(B_{i}\) 里)。\(A\) 表示所有 \(B_{i}\) 的最大值和次大值之和的可重集(当然也有其他维护方法)。

由于 multiset 常数太大,使用双堆来模拟。具体地,加入一个数时放在堆 \(x\) 里,删除一个数时放在堆 \(y\) 里,查询最大值时,比较两个堆的堆顶,如果相同就同时弹出,直到堆顶不同为止,此时堆 \(x\) 的堆顶就是最大值。删除最大值同理。时间复杂度同样为 \(O(n + m \log^2 n)\)。只不过堆比 multiset 快了 \(1\) 倍。
代码:
#include<bits/stdc++.h>
#define N 100005
using namespace std;int n, m, Q;
vector<int>p[N];int top[N], fa[N], dep[N], siz[N], son[N];
void dfs1(int x, int father) {fa[x] = father;dep[x] = dep[father] + 1;siz[x] = 1;int Maxson = -1;for(auto y : p[x]) {if(y == father) continue;dfs1(y, x);siz[x] += siz[y];if(siz[y] > Maxson) {Maxson = siz[y];son[x] = y;}}
}
void dfs2(int x, int topf) {top[x] = topf;if(son[x]) dfs2(son[x], topf);for(auto y : p[x]) {if(top[y]) continue;dfs2(y, y);}
}
int lca(int x, int y) {while(top[x] != top[y]) {if(dep[top[x]] < dep[top[y]]) swap(x, y);x = fa[top[x]];}return dep[x] < dep[y] ? x : y;
}
int dis(int x, int y) {return dep[x] + dep[y] - 2 * dep[lca(x, y)];
}int Fa[N], vis[N], root, Num, sum;
void Getroot(int x, int fa) {siz[x] = 1;int Maxsiz = 0;for(auto y : p[x]) {if(y == fa || vis[y]) continue; Getroot(y, x);siz[x] += siz[y];Maxsiz = max(Maxsiz, siz[y]);}Maxsiz = max(Maxsiz, sum - siz[x]);if(Maxsiz < Num) {Num = Maxsiz;root = x;}
}
void Build(int x) {vis[x] = 1;for(auto y : p[x]) {if(vis[y]) continue;Getroot(y, 0); //注意要先算出子连通块大小, 再去找重心 Num = 1e9, sum = siz[y];Getroot(y, 0);Fa[root] = x;Build(root);}
}int ljm[N], tot;struct Set { //双堆模拟set priority_queue<int>x, y;void Add(int a) { //加入a x.push(a);}void Del(int a) { //删除a y.push(a);}int Top() { //求最大值 while(y.size() && x.top() == y.top()) x.pop(), y.pop();return x.top();}void Pop() { //删除最大值 while(y.size() && x.top() == y.top()) x.pop(), y.pop();x.pop();}int Size() { //求集合大小 return x.size() - y.size();}int SecTop() { //求次大值 int A = Top(); Pop();int B = Top(); Add(A);return B;}
}C[N], B[N], A; //C[u]表示u子树内所有点距离Fa[u]的集合, B[u]表示u的儿子的C[u]的最大值的集合, A 表示 B[u]最大值和次大值 ;int Get_B(int x) {return B[x].Top() + B[x].SecTop();
}int Get_C(int x) {return C[x].Top();
}void upd(int x) {int i = x;if(B[i].Size() >= 2) A.Del(Get_B(i)); //删原来Aif(ljm[i] == 0) B[i].Add(0);else B[i].Del(0);if(B[i].Size() >= 2) A.Add(Get_B(i)); //加现在Awhile(Fa[x]) {if(B[Fa[x]].Size() >= 2) A.Del(Get_B(Fa[x])); //删原来Aif(C[x].Size()) B[Fa[x]].Del(Get_C(x)); //删原来Bif(ljm[i] == 0) C[x].Add(dis(i, Fa[x])); else C[x].Del(dis(i, Fa[x])); //更新Cif(C[x].Size()) B[Fa[x]].Add(Get_C(x)); //加现在Bif(B[Fa[x]].Size() >= 2) A.Add(Get_B(Fa[x])); //加现在Ax = Fa[x];}if(ljm[i] == 0) tot++;else tot--;ljm[i] ^= 1;
}int query() {if(tot == 0) return -1;else if(tot == 1) return 0;else return A.Top();
}void work() {for(int i = 1; i <= n; i++) upd(i);cin >> Q;while(Q--) {char opt;cin >> opt;if(opt == 'C') {int x;cin >> x;upd(x);}else cout << query() << endl;}
}signed main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n;for(int i = 1, u, v; i < n; i++) {cin >> u >> v;p[u].push_back(v);p[v].push_back(u); }dfs1(1, 0);dfs2(1, 1);Num = 1e9, sum = n; Getroot(1, 0);Build(root);work();return 0;}