想法还是太过于巧妙了。
首先有一个很简单的容斥 \(n^2\) 做法。
然后我们能发现 \(mod\) 很小,注意:\(\forall_{1 \le i < mod}\) \(C_{mod}^{i} = 0\)。
所以就有个天才的做法,将矩阵沿着对角线切开,类似这样:
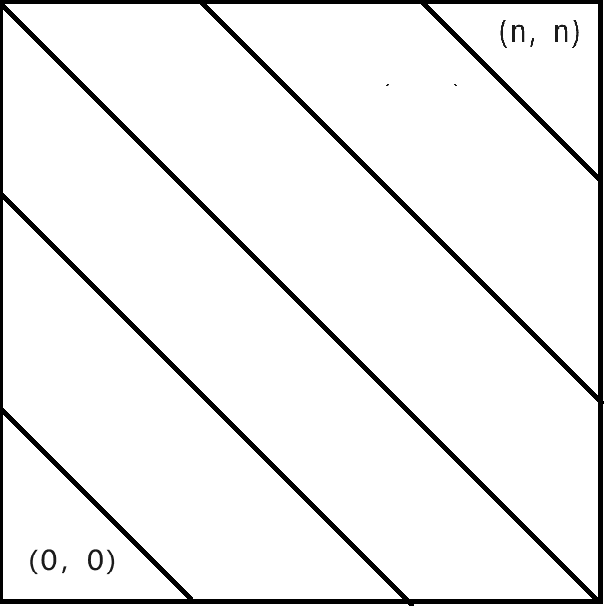
如果我们每隔 \(mod\) 进行一次切割,那么我们就会发现如果把第 \(i\) 条对角线转移到 第 \(i+1\) 条的话,就像这样:
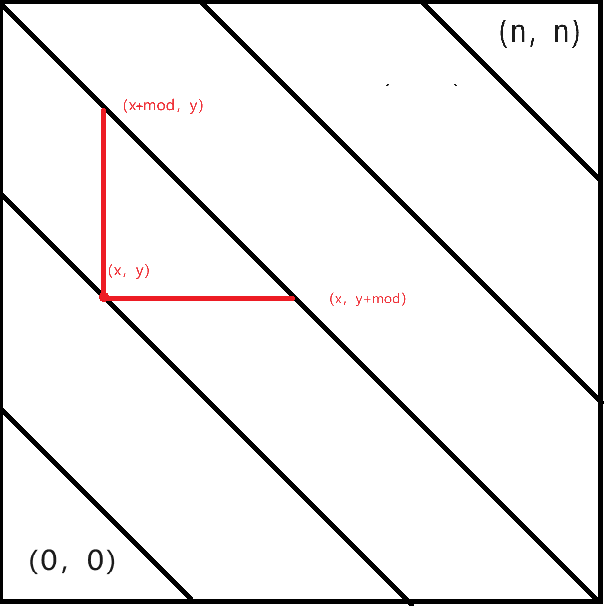
我们发现对于 \((x,y)\) 只需要转移到 \((x+mod,y)\) 和 \((x,y+mod)\) 就行了,因为其他点的组合数为 \(0\) !
所以 \(dp_{x,i}\) 表示点 \((i,x-i)\) 的方案数,然后转移就是:
- 对角线到对角线
- 对角线到障碍点
- 障碍点到障碍点
- 障碍点到对角线
分别做一下就行了。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int read(){int x=0,f=1; char c=getchar();while(!isdigit(c)){if(c=='-') f=-1; c=getchar();}while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48); c=getchar();}return x*f;
}
const int N=3e5+5,mod=509,M=2e5+5;
int n,a[N];
int cc[mod+5][mod+5];
inline int C(int x,int y){return cc[x][y];}
inline void init(){cc[0][0]=1;for(int i=1;i<=mod;i++){cc[i][0]=1;for(int j=1;j<=mod;j++) cc[i][j]=(cc[i-1][j]+cc[i-1][j-1])%mod;}
}int f[N],tmp[N],g[N];vector<int> s[N*2];
signed main(){n=read();for(int i=1;i<=n;i++) a[i]=read(),s[i+a[i]].push_back(i);init(),f[0]=1;for(int i=1;i<=2*n/mod;i++){int l=(i-1)*mod,r=i*mod;int pl=max(0ll,l-n),pr=min(l,n);int ll=max(0ll,r-n),rr=min(r,n);//line to linefor(int j=ll;j<=rr;j++){tmp[j]=f[j];if(j>=mod) (tmp[j]+=f[j-mod])%=mod; }for(int j=l+1;j<=r;j++){for(auto x:s[j]){int L=l-a[x],R=x;//point to pointfor(int k=L;k<R;k++) if(l<k+a[k]&&k+a[k]<=r&&a[k]<=a[x]) (g[x]-=g[k]*C(x-k+a[x]-a[k],x-k))%=mod; //(k,a[k]) (x,a[x])//line to pointfor(int k=max(pl,L);k<=min(R,pr);k++) (g[x]+=f[k]*C(x+a[x]-l,x-k))%=mod; //(k,(i-1)*mod-k) (x,a[x])g[x]=(g[x]+mod)%mod;//point to lineL=x,R=r-a[x];for(int k=max(L,ll);k<=min(R,rr);k++) (tmp[k]-=g[x]*C(r-a[x]-x,k-x))%=mod; //(x,a[x]) (k,i*mod-k)}}for(int i=0;i<=rr;i++) f[i]=(tmp[i]+mod)%mod,tmp[i]=0;}cout<<(f[n]+mod)%mod<<'\n';
}
/*
5
2 4 1 1 2
*/