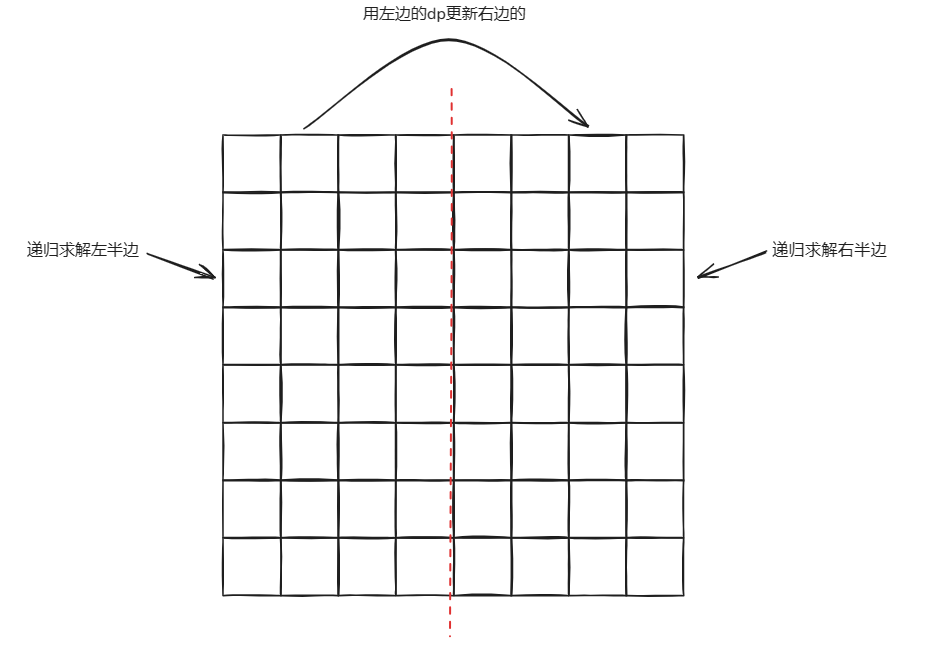
信息学奥赛初赛天天练-86-NOIP2014普及组-基础题5-球盒问题、枚举算法、单源最短路、Dijkstra算法、Bellman-Ford算法
PDF文档公众号回复关键字:20240908

1 NOIP 2014 普及组 基础题5
21 把 M个同样的球放到 N个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的放置方法?
(用 K表示)( )
例如,M=7,N=3 时,K=8;在这里认为 (5,1,1)和 (1,5,1)是同一种放置方法。
问:M=8,N=5时,K=( )
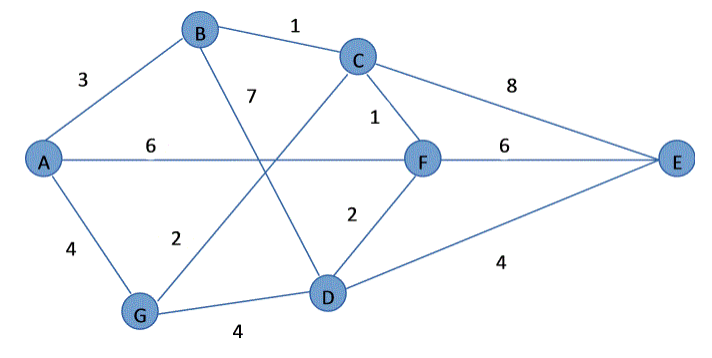
22 如图所示,图中每条边上的数字表示该边的长度,则从A到E的最短距离是
2 相关知识点
1) 枚举算法
枚举法是训练我们逻辑思维严密性的一种数学逻辑
在计算的过程中,我们一定要遵循枚举法的思路,把所有的情况,按照一定的顺序,一一列举出来
所以我们在学习枚举法的时候,一定要从小到大一一列举,不重不漏
例题
有红色和蓝色两种文具盒,小黄人要把8只相同的铅笔放到这两个文具盒中,每个文具盒至少放一支铅笔,那么一共有多少种不同的方法?
答案 7种
分析
红色和蓝色总共8只
每个文具盒子至少一只,固定红色最少1只,最多7只,从红色从小到大顺序枚举,可以做到不重不漏
总共有红色和蓝色2种,红色固定后,蓝色也固定了
红色 蓝色1 72 63 54 45 36 27 1
2) 单源最短路
单源最短路算法计算了图论中的一个经典问题,给出从给定的一个节点(称为源节点)出发到其余各节点的最短路径长度。
单源最短路算法适用于网络路由、路径设计等场景。Bellman-Ford算法和Dijkstra算法都是求解图的最短路径的算法
Dijkstra算法
Dijkstra算法的特点主要是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法采用的是贪心策略,其基本算法思想是指定起点s,再引进2个集合S和U,S用来记录已经找到最短路径的顶点,而U里包含未找到最短路径的顶点。系统不断地找出路径最短的顶点,并且将其移出U集,加入S集中。初始时S为空集,U集包含全部顶点,系统不断执行,遍历完所有顶点后,U集更新为空集,任务结束。
Bellman-Ford算法
Bellman-Ford算法的原理是连续地进行松弛,在每次松弛时更新每条边,若在n-1次松弛后还能更新,说明图中有负环,因此无法得出结果,否则任务完成。Bellman-Ford算法首先计算除源点外的所有顶点的最短距离估计值,然后对边集中的每条边进行松弛操作,使得每个顶点距离源点的最短距离估计值逐渐逼近其实际的最短距离
3 思路分析
21 把 M个同样的球放到 N个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的放置方法?
(用 K表示)( )
例如,M=7,N=3 时,K=8;在这里认为 (5,1,1)和 (1,5,1)是同一种放置方法。
问:M=8,N=5时,K=( 18 )
分析
枚举-非递减整数枚举
允许空着不放
5个袋子,可以放1个袋子,空4个袋子
8
总共1种5个袋子,可以放2个袋子,空3个袋子
1 7
2 6
3 5
4 4
总共4种5个袋子,可以放3个袋子,空2个袋子
1 1 6
1 2 5
1 3 4
2 2 4
2 3 3
总共5种5个袋子,可以放4个袋子,空1个袋子
1 1 1 5
1 1 2 4
1 1 3 3
1 2 2 3
2 2 2 2
总共5种5个袋子,可以放5个袋子,空0个袋子
1 1 1 1 4
1 1 1 2 3
1 1 2 2 2
总共3种
22 如图所示,图中每条边上的数字表示该边的长度,则从A到E的最短距离是( 11 )
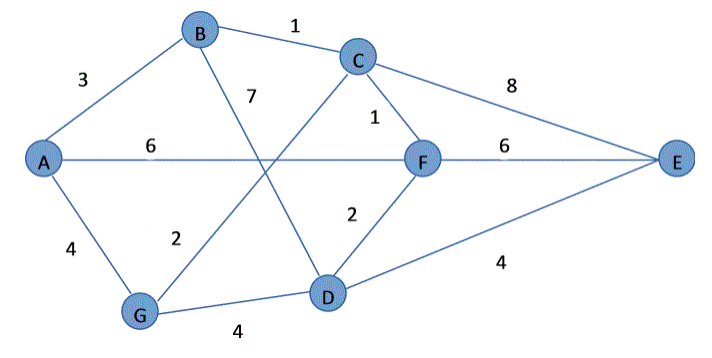
分析
从A出发,和A相邻的点为B,G,F,到B最短,长度为3
从A-B出发,和C,D相邻,到C最短,长度为3+1=4
从A-C出发,和E,F,G相邻,到F最短,长度为4+1=5
从A-F出发,和D,E相邻,到D最短,长度为5+2=7
从A-F出发,和D,E相邻,到E的长度为5+6=11
从A-D出发,到E距离为4,长度为7+4=11
所以最短距离为11

![[C++ Daily] 虚表与虚指针的理解](https://img2023.cnblogs.com/blog/3175458/202409/3175458-20240908121824651-1302536947.png)



![[Spring]MyBatis的执行原理](https://img2024.cnblogs.com/blog/1533409/202409/1533409-20240908104104398-396395653.png)