- Pre
- T1.不相邻集合
- 题目描述
- 部分分
- 40pts
- 10pts
- 正解
- 思路
- 代码
- T2.线段树
- 题目描述
- 部分分
- 20pts
- 正解
- 思路
- 代码
- T3.
- 部分分
- 40pts
- 正解
- 思路
- 代码
- 部分分
- T4.
- 部分分
- 10pts
- 正解
- 思路
- 代码
- 部分分
- And
Pre

赛时没有第一时间找到签到题,遂四处游走,后来决定先打T1,约1h时切了,然后1h打后3题暴力,后面推了推T4一个特殊性质,推了推T2一个特殊性质,但是T2的推假了。不太清楚怎么就来到了最后半小时,推T2的第二个特殊性质,未果,最后15min想到了T4的 \(O(n^2)\) 暴力但是没打完,算挂分吗。
T1.不相邻集合
题目描述
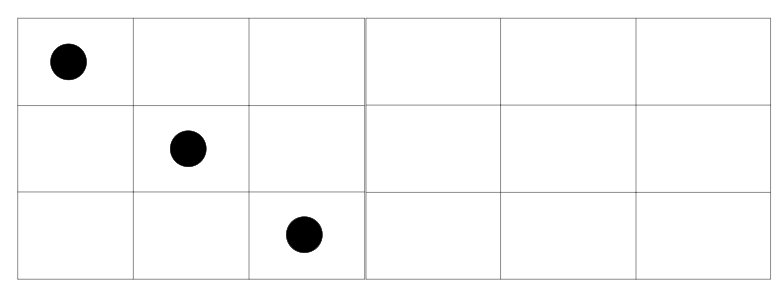
定义一个可重集合是不相邻集合当且仅当集合中任意两个数的差 \(\ge2\)。现在给你一个序列 \(a\),对于它的所有前缀求能组成的最大的不相邻集合的大小。
部分分
40pts
\(O(n^2)\) DP。设 \(dp[i][0]\) 表示以 \(i\) 值开头的最大不相邻集合的大小,\(dp[i][1]\) 表示以 \(i\) 值结尾的最大不相邻集合的大小,则有转移:
注意 \(+1\) 一定要放在取max外面。
10pts
在所有 \(a_i\) 都是奇数的情况下,我们任选不重复的数它们的差都一定 \(\ge2\),去重后直接统计即可。
正解
思路
对40pts的暴力进行优化。首先,重复的元素绝对没有任何贡献,所以仿照10pts的处理,先去重,也就是如果有重复的数,直接输出旧有的答案,然后不进行任何处理。
发现复杂度瓶颈在转移,有 \(O(n)\) 的遍历取max。区间最大值使我们想到线段树,于是这个东西用两颗线段树维护,支持单点赋值、区间查找最大值,复杂度 \(O(n\log n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a,b[300003],mx,mn,num;
bool use[500005];
struct XDS
{#define N 2200022int left[N],right[N],num[N];il int lft(int x){return x<<1;}il int iht(int x){return x<<1|1;}il void pu(int x){num[x]=max(num[lft(x)],num[iht(x)]);}void make(int x,int lt,int rt){left[x]=lt;right[x]=rt;if(lt==rt){num[x]=0;return;}ri me=(lt+rt)>>1;make(lft(x),lt,me);make(iht(x),me+1,rt);pu(x);}void add(int x,int pl,int y){if(left[x]==right[x]){num[x]=y;return;}ri me=(left[x]+right[x])>>1;if(pl<=me){add(lft(x),pl,y);}else{add(iht(x),pl,y);}pu(x);}int found(int x,int lt,int rt){if(lt>rt){return 0;}if(lt<=left[x]&&right[x]<=rt){return num[x];}ri me=(left[x]+right[x])>>1,rn=-inf;if(lt<=me){rn=max(rn,found(lft(x),lt,rt));}if(rt>me){rn=max(rn,found(iht(x),lt,rt));}return rn;}#undef N
}tree[2];
int main()
{scanf("%d",&a);mx=-inf,mn=inf;for(ri i=1;i<=a;i++){scanf("%d",&b[i]);mx=max(mx,b[i]);mn=min(mn,b[i]);}tree[0].make(1,1,mx);tree[1].make(1,1,mx);for(ri i=1;i<=a;i++){if(use[b[i]]){printf("%d ",num);continue;}use[b[i]]=true;ri j=tree[0].found(1,b[i]+2,mx);tree[0].add(1,b[i],j+1);num=max(num,j+1);j=tree[1].found(1,mn,b[i]-2);tree[1].add(1,b[i],j+1);num=max(num,j+1);printf("%d ",num);}return 0;
}
T2.线段树
题目描述
void build(int i, int l, int r) {L[i] = l; R[i] = r;if (l == r) return;int mid = (l+r)/2;build(i*2, l, mid); build(i*2+1, mid+1, r);
}
以上面的代码运行一遍build(1,1,n),求 \(\sum\limits_{i\in[x,y]}i\),答案 \(\bmod 10^9+7\)。\(1\le x\le y\le n\le 10^{18}\)。
部分分
20pts
暴力建树,统计区间和,复杂度 \(O(n\log n)\)。
正解
思路
发现复杂度主要来源于建树,考虑省略这一步,也就是 \(O(1)\) 求解某点的权值。设 \(f()\) 表示在一定条件下以某位置为根的总贡献,首先可知这个东西只和区间长度 \(n\) 和根值 \(x\) 有关,所以设为 \(f(n,x)\)(因为 \(n\) 值定了,以其为根的树的形态就定了;此时很显然它的左右儿子的值可以用根值表示,而下面的后代又可以被其左右儿子的值表示,以此类推,只要 \(n,x\) 定了,\(f()\) 的值就定了)。
然后通过理性分析||打表找规律,发现当 \(n\) 值定了以后,\(f(n,x)\) 是关于 \(x\) 的一次函数。
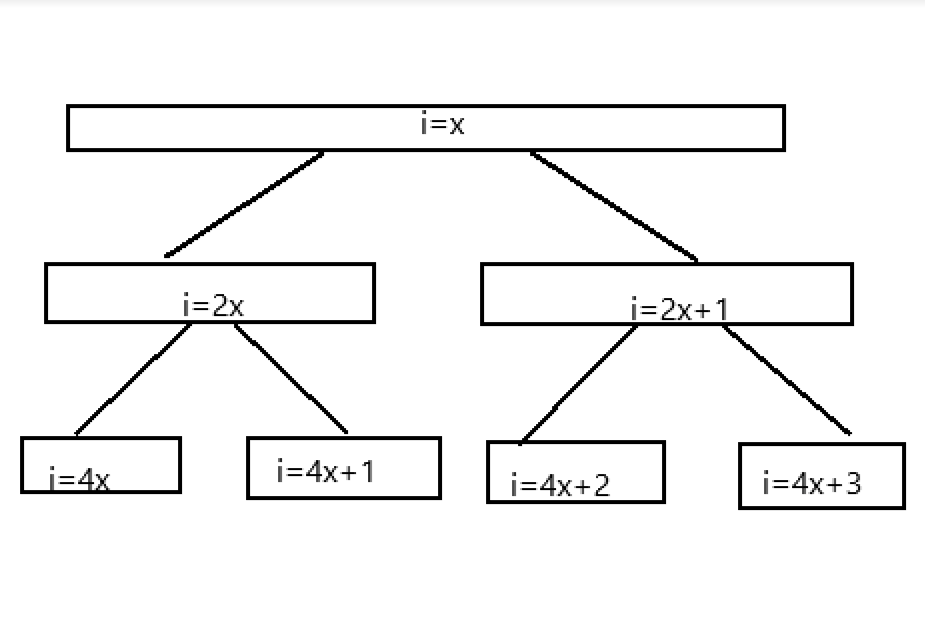
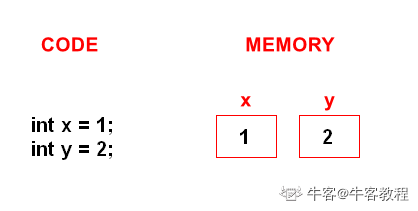
这是初始树。
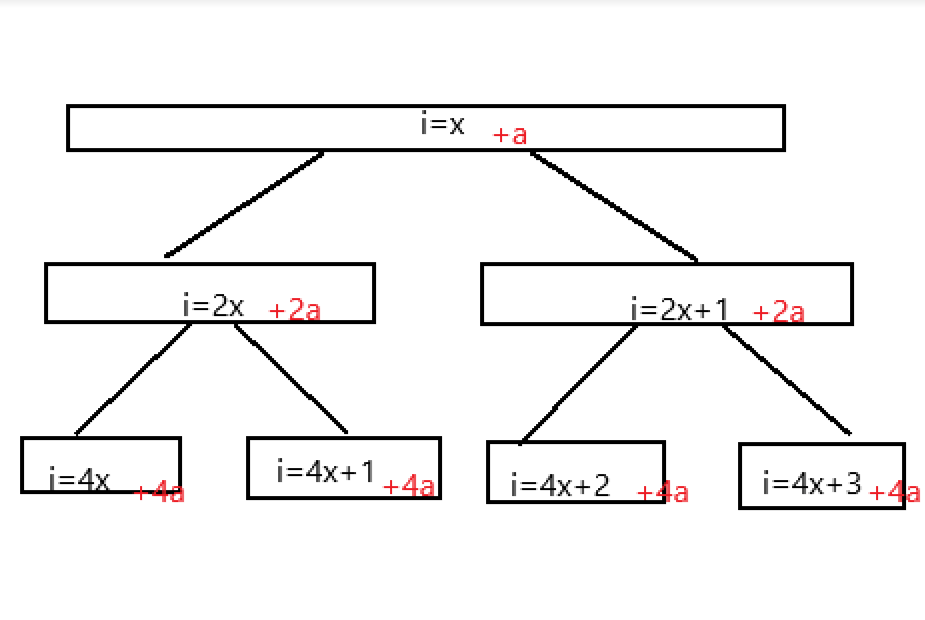
这是改变后的树。发现当根值 \(+a\),\(f(n,a)\)一定加的是 \(ka\),这时 \(f(n,x)\) 显然是一个一次函数,且这个 \(k\) 貌似只和树的形态有关系,也就是只和 \(n\) 有关系。\(x=0\) 时取到的\(b\)值同理,也只和 \(n\) 有关系。
设 \(f(n,x)=k_nx+b_n\),已知一个重要等式:
左右两边同时展开,得:
合并同类项,得:
由于是一次函数相同,所以 \(k,b\) 得分别相同,也就是:
然后就可以使用记搜 \(O(\log n)\) 的复杂度内求解线段树上一个节点的贡献了。外层还是线段树的查询,只不过不建树,递归记录区间左右端点,找到合法区间直接原地统计答案,所以再带上外层线段树的 \(\log n\),总复杂度 \(O(T\log^2n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define inf 0x3f3f3f3f
int a;
const int mod=1e9+7;
long long b,c,d;
map<long long,long long>kk,bb;
il long long K(long long x)
{if(x==1){return 1;}if(kk[x]){return kk[x];}kk[x]=((K(x>>1)<<1)+(K(((x+1)>>1))<<1)+1)%mod;return kk[x];
}
il long long B(long long x)
{if(x==1){return 0;}if(bb[x]){return bb[x];}bb[x]=(B(x>>1)+B((x+1)>>1)+K(x>>1))%mod;return bb[x];
}
il long long got(long long x,long long y)
{return (K(x)*y+B(x))%mod;
}
long long found(long long x,long long lt,long long rt,long long left,long long right)
{if(lt<=left&&right<=rt){return got(right-left+1,x);}register long long me=(left+right)>>1,rn=0;if(lt<=me){rn+=found((x<<1)%mod,lt,rt,left,me);rn%=mod;}if(rt>me){rn+=found((x<<1|1)%mod,lt,rt,me+1,right);rn%=mod;}return rn;
}
int main()
{scanf("%d",&a);while(a--){scanf("%lld%lld%lld",&b,&c,&d);printf("%lld\n",found(1,c,d,1,b));}return 0;
}