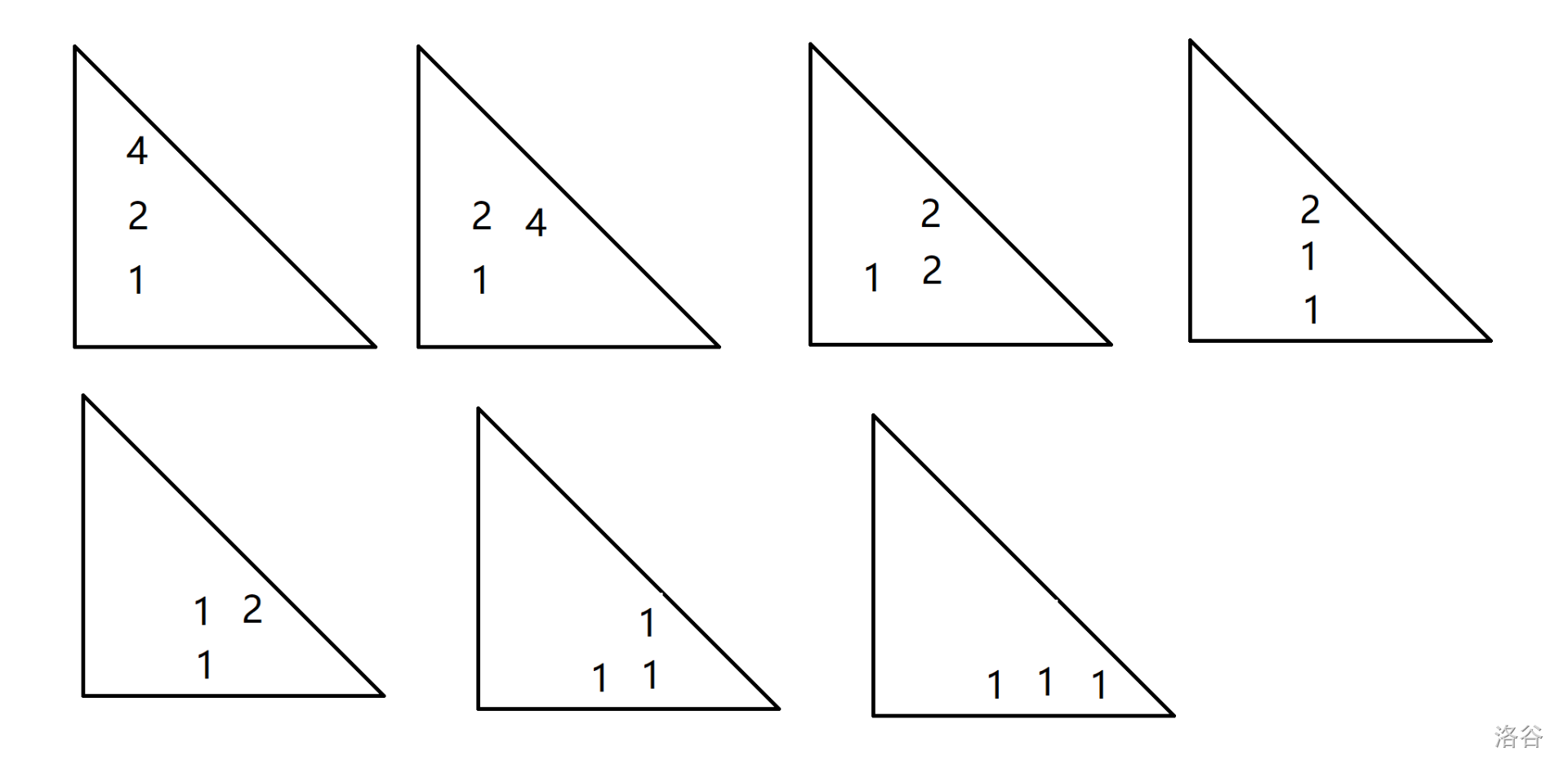
A - Full House
题目大意
来自一个掼蛋爱好者的翻译qwq
给定一副扑克牌中五张牌的编号\(A,B,C,D,E\),判断这五张是否为一组“三带二”。(不懂的自行百度
数据范围:\(1\le A,B,C,D,E\le 13\),且\(A,B,C,D,E\)不会全部相同。
输入格式
\(A~B~C~D~E\)
输出格式
如果是“三带二”,输出Yes;否则,输出No。
样例
| \(A\) | \(B\) | \(C\) | \(D\) | \(E\) | 输出 |
|---|---|---|---|---|---|
| \(1\) | \(2\) | \(1\) | \(2\) | \(1\) | Yes |
| \(12\) | \(12\) | \(11\) | \(1\) | \(2\) | No |
分析
嘿嘿,被自己的翻译给笑喷了吓住了,从来没见过这么好垃圾的翻译!
话不多说,这A题就是水(虽然studentWheat这位大佬还WA了3次,具体怎么WA的请大家好好学学引以为戒),解法很多,但是个人感觉还是直接统计一下来得简单明了,见代码。
代码
#include <cstdio>
using namespace std;int cnt[13];int main()
{for(int i=0; i<5; i++){int x;scanf("%d", &x);cnt[--x] ++;}bool has2 = false, has3 = false;for(int i=0; i<13; i++)if(cnt[i] == 2) has2 = true;else if(cnt[i] == 3) has3 = true;puts(has2 && has3? "Yes": "No");return 0;
}
B - Ancestor
题目大意
有\(N\)个人,第\(i\)个人的父/母是\(P_i\),题目保证\(P_i<i\)。
问:第\(N\)个人是第\(1\)个人的第几代?
\(2\le N\le 50\)
\(1\le P_i<i\)
输入格式
\(N\)
\(P_2~P_3~\dots~P_N\)
输出格式
输出答案。
分析
本题可以使用\(\text{DFS}\),但没有必要。题目限制条件特别给出了\(P_i<i\),因此如果按输入顺序依次处理每个人的世代,一个人的父亲肯定在这个人之前被考察到。
下面来看详细过程。
我们设\(\text{depth}_i=~\)第\(i\)个节点的深度,因此答案为\(\text{depth}_N\)。
初始时,\(\text{depth}_0=0\)。对于\(i=1\dots N\),依次设置\(\text{depth}_i:=\text{depth}_{P_i}+1\)。
最终,输出结果即可。总时间复杂度为\(\mathcal O(N)\)。
代码
#include <cstdio>
#define maxn 55
using namespace std;int dep[maxn];int main()
{int n;scanf("%d", &n);for(int i=1; i<n; i++){int f;scanf("%d", &f);dep[i] = dep[--f] + 1;}printf("%d\n", dep[n - 1]);return 0;
}
C - Monotonically Increasing
题目大意
输出所有的长度为\(N\)的严格上升的序列,其中每个元素都在\([1,M]\)之间,按字典升序输出,\(1\le N\le M\le 10\)。
输入格式
\(N~M\)
输出格式
按字典升序输出所有符合条件的序列,一行一个,序列中的每个元素用空格分隔。
分析
基础的回溯算法题,见代码。
代码
#include <cstdio>
#define maxn 15
using namespace std;int n, m, ans[maxn];void dfs(int pos, int last)
{if(pos == n){for(int i=0; i<n; i++)printf("%d ", ans[i]);putchar('\n');return;}while(++last <= m){ans[pos] = last;dfs(pos + 1, last);}
}int main()
{scanf("%d%d", &n, &m);dfs(0, 0);return 0;
}
D - Left Right Operation
题目大意
给定长为\(N\)的整数序列\(A=(A_1,A_2,\dots,A_N)\)。
你可以进行下列两个操作,每个最多一次:
- 选择整数\(x\),将\(A\)的前\(x\)项全部改成\(L\)。
- 选择整数\(y\),将\(A\)的后\(y\)项全部改成\(R\)。
求操作后,最小的\(A\)中所有元素之和。
\(1\le N\le 2\times 10^5\)
\(-10^9\le L,R,A_i\le 10^9\)
输入格式
\(N~L~R\)
\(A_1~A_2~\dots~A_N\)
输出格式
输出答案。
分析
令\(f_i=(\)使用操作\(1\)选择\(x\le i\)时的前\(i\)个序列元素的最小和\()\),
\(~~~~g_i=(\)使用操作\(2\)选择\(y\le i\)时的后\(i\)个序列元素的最小和\()\),
则可得递推式\(f_i=\min\{f_{i-1}+A_i,L\times i\}\),\(g_i\)同理。
此时,枚举两种操作的分界点\(i\),则答案为\(\min\limits_{i=1}^N(f_i+g_{N-i})\)。实现时,可将\(g\)数组倒过来计算,这样答案为\(\min\limits_{i=1}^N(f_i+g_{i+1})\)。
递推式的正确性证明
前面已经提到了,\(f_i=\min\{f_{i-1}+A_i,L\times i\}\)。为什么?
先看\(\min\)后面的部分,应该好理解,就是前\(i\)个全部替换成\(L\)的总和。前面的\(f_{i-1}+A_i\)才是关键。考虑\(f_{i-1}\)的计算来源,要么是从\(f_{i-2}+A_{i-1}\)递推过来的,要么也是直接用\(L\times(i-1)\)得到的。再考虑\(f_{i-2},f_{i-3},\dots,f_1\)会发现,递推式的结果一定是(一段\(L\))+(一段\(A_i\))得到的。因此,这个递推式正确。\(g\)的正确性也可以用同样的方法证明,感兴趣的读者可以自行尝试。
总时间复杂度为\(\mathcal O(N)\)。
代码
注意使用long long。
#include <cstdio>
#define maxn 200005
using namespace std;using LL = long long;
inline LL min(const LL& x, const LL& y)
{return x < y? x: y;
}int a[maxn];
LL f[maxn], g[maxn];int main()
{int n, l, r;scanf("%d%d%d", &n, &l, &r);for(int i=0; i<n; i++)scanf("%d", a + i);f[0] = min(l, a[0]);for(int i=1; i<n; i++)f[i] = min(f[i - 1] + a[i], (i + 1LL) * l);for(int i=n-1; i>=0; i--)g[i] = min(g[i + 1] + a[i], LL(n - i) * r);LL ans = g[0];for(int i=0; i<n; i++)ans = min(ans, f[i] + g[i + 1]);printf("%lld\n", ans);return 0;
}
E - Sugoroku 3
题目大意
有\(N\)个方格,分别是方格\(1\),方格\(2\),..,方格\(N\)。
在方格\(1,2,\dots,N-1\)上,各有一枚骰子。方格\(i\)上的骰子会按照相同的概率随机输出\(0,1,\dots,A_i\)中的一个。
直到到达方格\(N\)之前,你每次会前进骰子输出的步数。换句话说,如果你在方格\(x\)上(\(1\le x<N\)),骰子输出了数字\(y\)(\(0\le y\le A_i\)),你下一步会到达方格\(x+y\)。
求到达方格\(N\)步数的期望值,对\(998244353\)取模。
\(2\le N\le 2\times 10^5\)
\(1\le A_i\le N-i\)(\(1\le i<N\))
有理数取模【洛谷模板:P2613】
任意一个有理数都可被表示为\(\frac PQ\)的形式。令\(R\)为取模的结果,则\(R\times Q\equiv P~(\bmod~998244353)\)。
友情提示:对于除法计算,如\(\frac AB\)计算时,改为\(A\times B^{P-2}\bmod P\),其他逐步取模即可。本题中,\(P=998244353\)。
输入格式
\(N\)
\(A_1~A_2~\dots~A_{N-1}\)
输出格式
输出答案,对\(998244353\)取模。
分析
令\(\text{dp}_i=~\)从\(i\)到\(N\)的期望步数,则初始状态为\(\text{dp}_N=0\),答案为\(\text{dp}_1\)。
由于在方格上不能倒退,因此考虑倒序计算\(\text{dp}\)。对于第\(i\)个点,易得
其中,求和即遍历后面每一个下一步可能到达的位置,乘上出现概率\(\frac1{A_i+1}\),最后再加上\(1\)表示使用一步。
由于左右都有\(\text{dp}_i\),无法直接计算,我们将其单独提出并解方程,得:
此时,时间复杂度为\(\mathcal O(N^2\log P)\)(快速幂inv操作需要\(\log P\)的时间,其中\(P=998244353\)),使用后缀和优化后可达\(\mathcal O(N\log P)\),可以通过本题。
代码
#include <cstdio>
#define maxn 200005
#define MOD 998244353
using namespace std;using LL = long long;
int a[maxn], suf[maxn];inline int inv(LL x)
{LL res = 1LL;int p = MOD - 2;while(p){if(p & 1) (res *= x) %= MOD;(x *= x) %= MOD, p >>= 1;}return res;
}int main()
{int n, cur;scanf("%d", &n);for(int i=0; i<n-1; i++)scanf("%d", a + i);for(int i=n-2; i>=0; i--){int t = suf[i + 1] - suf[i + 1 + a[i]];if(t < 0) t += MOD;cur = (a[i] + t + 1LL) % MOD * inv(a[i]) % MOD;if((suf[i] = suf[i + 1] + cur) >= MOD)suf[i] -= MOD;}printf("%d\n", cur);return 0;
}