前言
完全借鉴于 洛谷日报
前提条件
在一个网格图上, 每一次可以从 \((x,y)\) 走到 \((x+1,y-1)\) 或者 \((x+1,y-1)\) 限制是一条直线 \(y=k\)
题外话
我们其实可以发现这和每一次可以从 \((x,y)\) 走到 \((x+1,y)\) 或者 \((x, y+1)\) 限制是一条 \(45°\)的斜线 \(y=x+k\) 是等价的

我们发现我们要从原点走到红点,我们可以走的(其它路径走到后就肯定不会产生贡献)路径构成了一个斜着的矩形,这和另一种格路计数是等价的
总路径数
我们设 \(<a,b,c,d>\)表示从 \((a,b)\) 走到 \((c,d)\)的路径数
首先需要满足 \(a \le c\)
然后考虑我们走的步数是 \(c-a\) 步, 考虑设向上走的步数是 \(x\) 步, 则有 \(x - (c - a - x) = d - b\) , 解得 \(x = \frac{d-b+c-a}{2}\)
所以总方案数 \(<a,b,c,d> = {c-a\choose \frac{d-b+c-a}{2}}\)
特殊的当 \(d-b+c-a\) 为奇数的时候这个值为 \(0\)
与一条直线相交与不相交
我们用 \([a,b,c,d,k]\) 表示 从 \((a,b)\)走到 \((c,d)\) 与直线 \(y=k\)相交的方案数
\(\{a,b,c,d,k\}\) 与上述定义相反 为相交
我们需要分类讨论
- \(a \le k \le c\)
这个比较显然 \([a,b,c,d,k] = <a,b,c,d>\)
\(\{a,b,c,d,k\} = 0\)
- \(k < a\) 或者 \(c < k\)
然后就是反射容斥有 \([a,b,c,d,k] = <a,b,c, 2k - d>\) 或者我们也可以把 \((a,b)\) 对称过去, 有 \([a,b,c,d,k]=<a,2k-b,c,d>\)
\(\{a,b,c,d,k\} = <a,b,c,d> - [a,b,c,d,k]\)
与一条直线相交次数之和
我们只讨论从 \((0,0)\) 出发的情况
用 \([a,b,k]\) 表示从 \((0,0)\) 走到 \((a,b)\) 的所有路径与直线 \(y = k\) 相交的次数之和
首先分类讨论
- \(0 \le k \le a\)
然后我们考虑两种计算方法
另一种 我们设 \(res1\) 表示最后一个交点的贡献, \(res2\) 表示 剩下的交点个数的贡献
\(res1 = <0,0,a,b>\)
\(res2 = \sum_{i=0}^{a} <0,0,i,k> \times ([i+1, k-1, a, b,k] + [i+1, k+1, a, b, k])\)
后边的分讨是为了消除 \((i,k)\) 对于交点的影响, 根据上文有
\([i+1,k-1,a,b,k]=<i+1,k-1,a,b>\)
\([i+1,k+1,a,b,k] = <i+1, 2k- (k+1),a,b>=<i+1, k-1,a,b>\)
我们发现这是相等的
于是
\(res2 = \sum_{i=0}^{a} <0,0,i,k> \times 2 <i+1,k-1,a,b> = 2 \sum_{i=0}^{a}<0,0,i,k> \times < i,k,a-1,b+1>\)
那么第二种计算方法就是
我们发现这两种挺像的, 于是考虑一下递推, 设 \(F(a,b,k)=\sum_{i=0}^a <0, 0, i, k> \times <i,k,a,b>\)
那么就有 \(F(a,b,k)=<0,0,a,b>+ 2F(a-1,b+1,k)\)
边界就是 \(a-1 < 0\) 值为 \(0\)
那么我们把这个展开就是
相当于我们要求形如 \(\sum_{i=m}^n2^{n-i}{i\choose m}\) 的式子
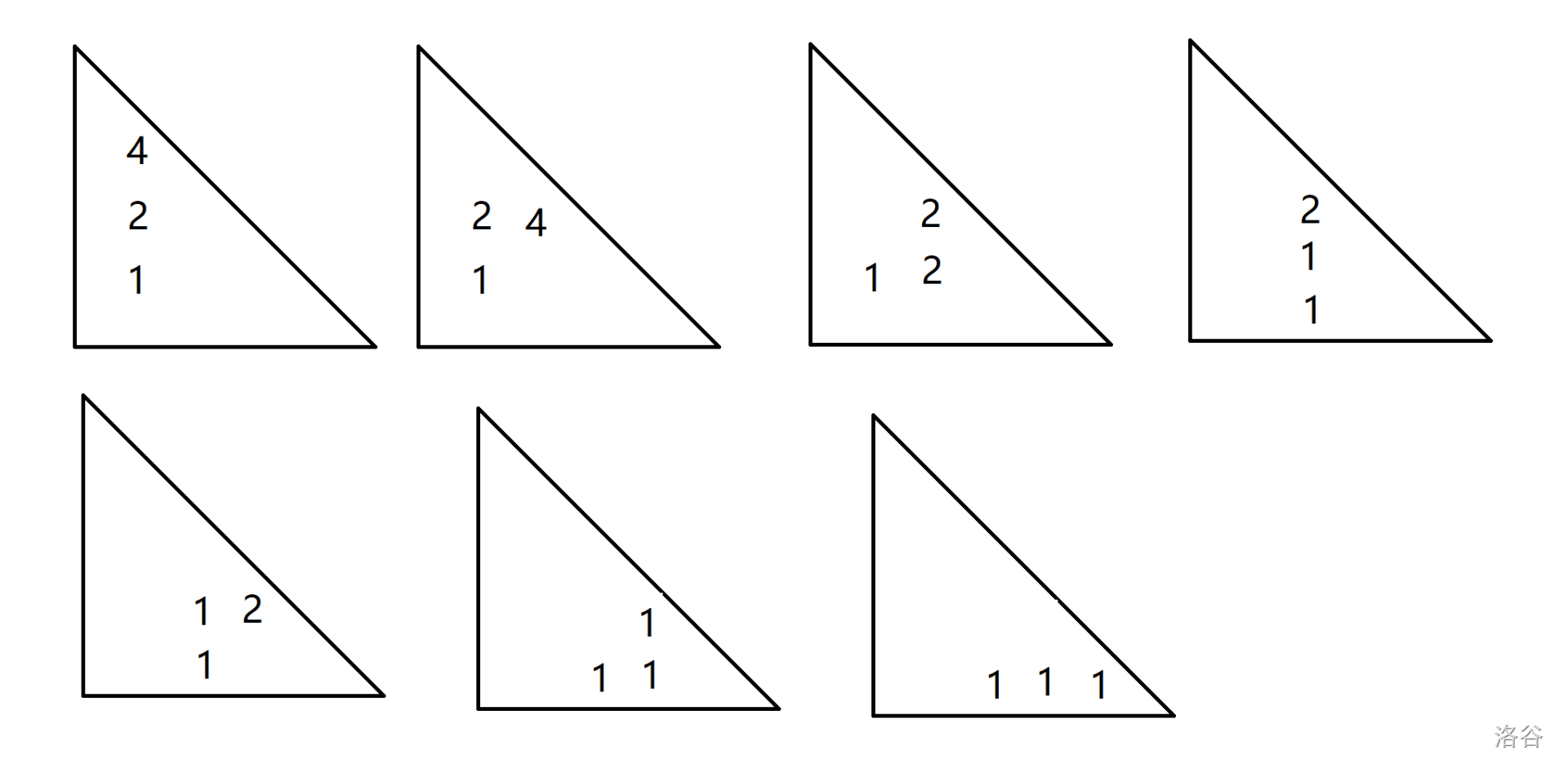
实际上就是 \(\sum_{i=m+1}^{n+1} {n+1\choose i}\)
- \(k > a\) 或者 \(k < 0\)
反射容斥即可, 因为反射之后该交还是交, 不交还是不交
\([a,b,k] = [a,2k-b,k]\)
其实还有 留给以后的自己 咕咕咕