【算法笔记】位运算详解

0. 前言

突然想到位运算是个好东西，就来水一波文章了……

注意：我把能想到的有关位运算的所有内容都放进来了，所以篇幅较长，请谅解！若有写的不清楚或者不够详细的地方欢迎在评论区补充，谢谢支持！

本文中参考代码均使用C++编写。

废话不多说，下面步入正题。

1. 基本运算

有一定基础的可以跳过该部分。

位运算的简要法则：
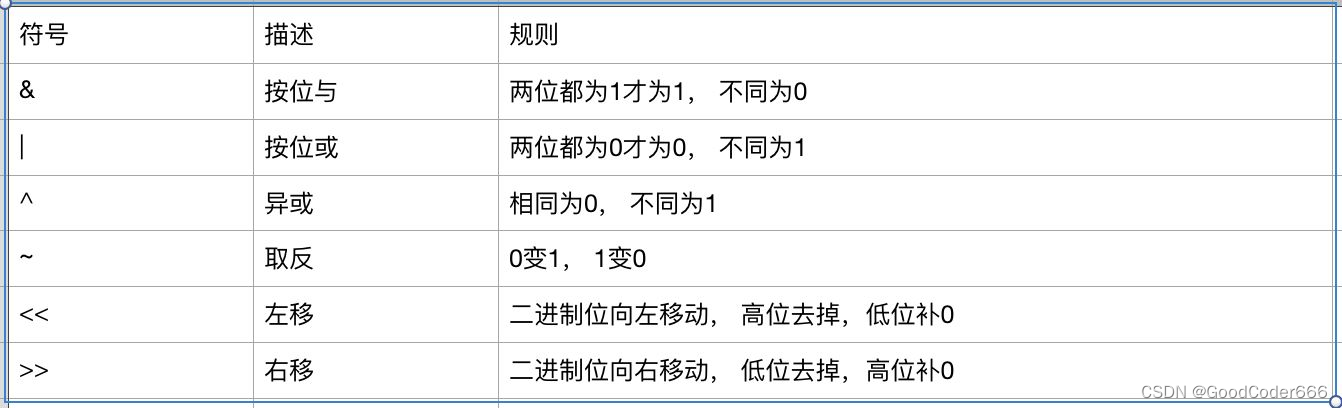
位运算法则-简要

详细解释：

1.1 取反

取反（~x）是最简单的位运算操作，只有一个参数\(x\)。将参数上的每一位对应取反即可。例如：
~0011 = 1100
~1011 = 0100
性质：~(~x) = x

1.2 按位与

按位与（x & y）有两个参数\(x\)和\(y\)。对于\(x\)和\(y\)中的每个对应位，参照下表输出到结果的对应位：

\(x\) \(y\) x & y
\(0\) \(0\) \(0\)
\(0\) \(1\) \(0\)
\(1\) \(0\) \(0\)
\(1\) \(1\) \(1\)

例子：
0011 & 1100 = 0000
1010 & 1011 = 1010

性质：

  • 交换律：a & b = b & a
  • 结合律：a & b & c = a & (b & c)
  • 自与：a & a = a
  • 与\(0\)：0 & a1 & a2 & a3 & ... = 0
  • 与\(\infty\)（全\(1\)）：a & inf = a

1.3 按位或

按位与（x | y）有两个参数\(x\)和\(y\)。对于\(x\)和\(y\)中的每个对应位，参照下表输出到结果的对应位：

\(x\) \(y\) x | y
\(0\) \(0\) \(0\)
\(0\) \(1\) \(1\)
\(1\) \(0\) \(1\)
\(1\) \(1\) \(1\)

例子：
1100 | 0011 = 1111
1010 | 0001 = 1011

性质：

  • 交换律：a | b = b | a
  • 结合律：a | b | c = a | (b | c)
  • 自或：a | a = a
  • 或\(0\)：a | 0 = a
  • 或\(\infty\)（全\(1\)）：a | inf = inf

1.4 异或

异或（\(x\oplus y\)或x ^ y）有两个参数\(x\)和\(y\)。对于\(x\)和\(y\)中的每个对应位，参照下表输出到结果的对应位：

\(x\) \(y\) \(x\oplus y\)
\(0\) \(0\) \(0\)
\(0\) \(1\) \(1\)
\(1\) \(0\) \(1\)
\(1\) \(1\) \(0\)

举例：
1000 ^ 1011 = 0011
0101 ^ 1010 = 1111

性质：

  • 交换律：\(a\oplus b=b\oplus a\)
  • 结合律：\(a\oplus b\oplus c=a\oplus(b\oplus c)\)
  • 自异或：\(a\oplus a=0\)
  • 异或\(0\)：\(a\oplus 0=a\)
  • 多重异或：\(a\oplus b\oplus b=a\oplus (b\oplus b)=a\oplus 0=a\)
  • 异或\(\infty\)（全\(1\)）：\(a\oplus \infty=~\)~a
  • 若\(a\oplus b=c\)，则\(a\oplus c=b\)。

1.5 位移

位移分为左移（<<）和右移（>>）。

  • a << b：将\(a\)末尾添上\(b\)个\(0\)的结果。
  • a >> b：从\(a\)末尾删掉\(b\)位的结果。

性质：

  • (a << b) >> b = a
  • a << b\(~=a\times 2^b\)
  • a >> b\(~=\lfloor\frac a {2^b}\rfloor\)

1.6 练习题

1.6.1 判断\(2\)的整数次幂

题意：给定整数\(N\)，判断其是否为\(2\)的整数次幂。

1.6.2 洛谷 P1100 高低位交换

题意：给定一个\(32\)位整数\(x\)，在二进制下交换其前\(16\)位与后\(16\)位，输出最终的数。

答案为ans = (x >> 16) | (x << 16)，这样解释：

数值 前\(16\)位 后\(16\)位
\(x\) \(A\) \(B\)
x >> 16 \(16\)个\(0\) \(A\)
x << 16 \(B\) \(16\)个\(0\)
ans \(B\) \(A\)

注意此处使用\(32\)位无符号整数进行计算，这样x << 16会自然溢出，导致前\(16\)位被丢弃，恰好满足要求。

参考程序：

#include <cstdio>
using namespace std;int main()
{unsigned int x;scanf("%u", &x);printf("%u\n", (x >> 16) | (x << 16));return 0;
}

1.6.3 找出不同的数

给定一个序列\(A=(A_1,A_2,\dots,A_{2N+1})\)，其中有\(N\)个数各出现\(2\)次，还有一个数正好出现\(1\)次。找到这个数。请尽可能优化程序的时间和空间复杂度。

- 时间\(\mathcal O(N)\)或\(\mathcal O(N\log N)\)，空间\(\mathcal O(N)\)解法
简单统计每个数的出现次数，最后找到正好出现\(1\)次的数。

- 时间\(\mathcal O(N)\)，空间\(\mathcal O(1)\)解法
考虑所有数的异或和\(S=A_1\oplus A_2\oplus\dots\oplus A_{2N+1}\)，则\(A\)中所有出现两次的数抵消为\(0\)，剩下的即为唯一出现一次的数，所以直接输出\(S\)即可。

参考程序：

#include <cstdio>
using namespace std;int main()
{int n;scanf("%d", &n);n = (n << 1) + 1;int ans = 0;while(n--){int x;scanf("%d", &x);ans ^= x;}printf("%d\n", ans);return 0;
}

1.6.4 AtCoder Beginner Contest 261 E - Many Operations

解法：对于\(i=1,2,\dots,N\)，记录操作\(1,2,\dots,i\)后每一位上的\(0\)和\(1\)分别变成什么，可以在\(\mathcal O(N)\)的时间内用类似于前缀和的方法完成；最后用位运算快速模拟\(N\)次连续操作即可，总时间复杂度为\(\mathcal O(N)\)。

// https://atcoder.jp/contests/abc261/submissions/33495431
#include <cstdio>
using namespace std;int main()
{unsigned n, c, zero = 0, one = 0xffffffff;scanf("%d%d", &n, &c);while(n--){int t, a;scanf("%d%d", &t, &a);if(t == 1) one &= a, zero &= a;else if(t == 2) one |= a, zero |= a;else one ^= a, zero ^= a;printf("%d\n", c = (c & one) | (~c & zero));}return 0;
}

2. 扩展概念&运算

2.1 lowbit

lowbit(x)即为二进制下\(x\)的最低位，如lowbit(10010) = 10、lowbit(1) = 1。严格来说\(0\)没有lowbit，部分情况下可视为lowbit(0) = 1。利用lowbit函数可实现树状数组等数据结构。

lowbit 计算方式

  1. 暴力计算
    简单粗暴的按位直接计算，如下：
    int lowbit(int x)
{int res = 1;while(x && !(x & 1))x >>= 1, res <<= 1;return res;
}
    时间复杂度\(\mathcal O(\log X)\)。缺点：速度慢，代码长，没有体现位运算的优势
  2. x & -x
    巧妙利用lowbit(x) = x & -x。感兴趣的读者可自行尝试证明。
    时间复杂度\(\mathcal O(1)\)。相比(1)来说，代码更短，速度更快。
  3. x & (x - 1)
    注意：x & (x - 1)不是lowbit(x)，而是x - lowbit(x)。
    这种方法常用于树状数组中，可提升x - lowbit(x)的计算速度。

2.2 popcount

popcount(x)定义为\(x\)在二进制下\(1\)的个数，如popcount(10101) = 3，popcount(0) = 0。

popcount 计算方式

  1. 暴力计算检查
    还是最粗暴的算法，通过枚举每一位并检查是否为\(1\)达到目的，时间复杂度为\(\mathcal O(\log X)\)。
    int popcount(int x)
{int res = 0;while(x){res += x & 1;x >>= 1;}return res;
}
  2. lowbit 优化
    时间复杂度还是\(\mathcal O(\log X)\)，不过平均用时会比(1)快2~3倍左右。
    int popcount(int x)
{int res = 0;for(; x; x&=x-1) res ++;return res;
}
  3. builtin 函数（最快）
    详见3.1 __builtin_popcount/__builtin_popcountll。

3. builtin 位运算函数

注意：后面带ll的传入long long类型，不带ll接受int类型。本部分内容按常用程度递减排序。
参考：https://blog.csdn.net/zeekliu/article/details/124848210

3.1 __builtin_popcount/__builtin_popcountll

返回参数在二进制下\(1\)的个数。

3.2 __builtin_ctz / __buitlin_ctzll

返回参数在二进制下末尾\(0\)的个数。

3.3 __buitlin_clz / __buitlin_clzll

返回参数在二进制下前导\(0\)的个数。

3.4 __builtin_ffs / __buitlin_ffsll

返回参数在二进制下最后一个1在第几位（从后往前）。
注意：一般来说，builtin_ffs(x) = __builtin_ctz(x) + 1。当\(x=0\)时，builtin_ffs(x) = 0。

3.5 __builtin_parity / __builtin_parityll

返回参数在二进制下\(1\)的个数的奇偶性（偶：0，奇：1），即__builtin_parity(x) = __builtin_popcount(x) % 2。
P.S. 这函数，不知是哪位神仙想出来的……

4. 位运算的应用

4.1 子集表示法

对于集合\(\{0,1,\dots,N-1\}\)，我们使用一个\(N\)位的二进制整数\(S\)来表示它的一个子集。从右往左第\(i\)位表示子集是否包含了\(i\)。容易发现，对于任意子集\(S\)，\(S\in [0,2^N-1]\)，且对于任意\(S\in [0,2^N-1]\)，\(S\)都是\(\{0,1,\dots,N-1\}\)的一个有效子集。下面我们来讲这种子集表示的具体操作。

4.1.1 子集操作

子集的操作如下（规定\(N\)为集合元素个数）：

  • 空集：\(0\)
  • 满集：\(2^N-1\)（\(N\)个\(1\)）
  • 集合\(S\)的元素个数：__builtin_popcount(S)或__builtin_popcountll(S)
  • 集合\(S\)是否包含\(i\)：S >> i & 1
  • 将\(i\)加入\(S\)（操作前\(S\)是否包含\(i\)不影响操作结果）：S |= 1 << i
  • 将\(i\)从\(S\)中删除（操作前\(S\)必须包含\(i\)）：S ^= 1 << i
  • 将\(i\)从\(S\)中删除（操作前\(S\)是否包含\(i\)不影响操作结果）：S &= ~(1 << i)
  • \(S\)和\(T\)的交集（\(S\)和\(T\)都包含的集合）：S & T
  • \(S\)和\(T\)的并集（\(S\)和\(T\)中有任意一个包含的集合）：S | T
  • \(S\)和\(T\)的差集（\(S\)和\(T\)中恰好有一个包含的集合）：S ^ T

4.1.2 子集枚举

讲了这么多，也该到子集的实际应用了吧。下面我们来看子集最初步的应用——子集枚举。

- 必会：枚举\(N\)个元素的所有子集
这个很简单，直接枚举\(S\in [0,2^N-1]\)即可。代码如下：

#include <cstdio>
using namespace std;const int N = 3;int main()
{printf("N = %d\n", N);for(int s=0, full=(1<<N)-1; s<=full; s++){printf("Subset %d:", s + 1);for(int i=0; i<N; i++)if(s >> i & 1)printf(" %d", i);putchar('\n');}return 0;
}

- 必会：枚举子集的子集
如果我们想枚举\(\{0,1,\dots,N-1\}\)的子集的子集，怎么办？这是一个经典套路，常用于状压DP，写法如下：

for(int S=0; S<(1<<N); S++) // 枚举子集Sfor(int T=S; T; T=(T-1)&S) // 枚举子集的子集T{// Do something...printf("%d\n", t);}

请注意：这个算法的时间复杂度为\(\mathcal O(3^N)\)，不是\(\mathcal O(4^N)\)，使用此算法时请准确估算时间复杂度。

- 扩展：枚举\(N\)个元素中大小为\(K\)的子集
首先很容易想到先枚举所有\(\{0,1,\dots,N-1\}\)的所有子集，再依次检查大小是否为\(K\)。代码如下：

for(int s=0; s<(1<<n); s++)
{int cnt = __builtin_popcount(s);if(cnt != K) continue;// Do something...
}

这种做法虽然正确，也很易懂，但可惜效率太低，\(2^N\)次popcount操作浪费了很多时间。我们考虑优化。《挑战程序设计竞赛》上给出了一种算法，如下：

int S = (1 << k) - 1;
while(S < 1 << n)
{// Do something...printf("%d\n", S);// 移到下一个合法子集int x = S & -S, y = S + x;S = ((S & ~y) / x >> 1) | y;
}

这样可保证每次枚举到的都是大小为\(K\)的子集，可以大大提高算法效率。

4.1.3 扩展：std::bitset

bitset，顾名思义，即为用位运算操作的集合。
对于元素个数\(N\in [1,64]\)，集合\(\{0,1,\dots,N-1\}\)的任意子集都可以用一个\(32\)或\(64\)位整数表示出来，操作时间复杂度为\(\mathcal O(1)\)。那么对于\(N>64\)，怎么办？我们可以用多个\(32\)或\(64\)位无符号整数拼凑为一个\(N\)位的bitset，容易发现其操作的时间复杂度为\(\mathcal O(\frac Nw)\)（\(N\)位的二进制数可用\(\lceil\frac Nw\rceil\)个\(w\)位无符号整数拼凑而成），其中\(w\)一般为\(32\)或\(64\)。

C++的Standard Template Library（STL）为我们提供了<bitset>头文件，用于bitset的定义。

用法如下：
bitset

用法示例：

#include <cstdio>
#include <bitset> // 头文件
using namespace std;int main()
{const int N = 500;bitset<N> S; // 定义大小为N的bitset S，初始为全0S.set(1);    // 将S的第1位设为1S[0] = 1;    // 将S的第0位设为1，注意bitset可使用下标访问和赋值S.reset(1);  // 将S的第1位设为0printf("S[1]: %d\n", (int)S[1]); // 输出S第2位上的值printf("Count: %d\n", (int)S.count()); // S的popcount（二进制下1的个数）printf("Size: %d\n", (int)S.size()); // S的二进制位数（N）printf("None? %d\n", (int)S.none()); // S是否为空？printf("Any?  %d\n", (int)S.any());  // S是否有1？bitset<N> T; // 定义一个新的bitset -- TT.set(); // T置为全1S.set(2), T.reset(2);printf("Intersection: %d\n", (int)(S & T).count()); // 交集printf("Union: %d\n", (int)(S | T).count()); // 并集printf("Difference: %d\n", (int)(S ^ T).count()); // 差集return 0;
}
习题：AtCoder Beginner Contest 258 G - Triangle

题意和解法见https://blog.csdn.net/write_1m_lines/article/details/125582361#t15。

4.2 深度优先搜索（DFS）的位运算优化

本算法其实还是二进制表示子集的一种优化，不过内容较多，所以单独放了出来。

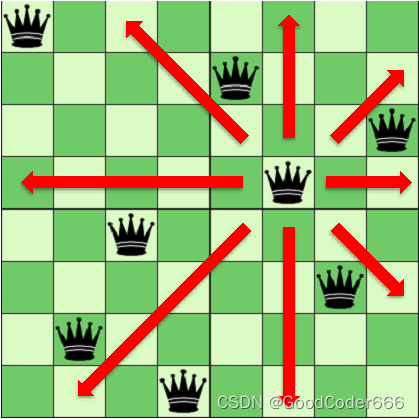
考虑经典的八皇后问题：

有一个\(8\times 8\)的国际象棋棋盘，要在其中摆\(8\)个皇后，求有多少种不同的摆法，使得任意两个皇后之间都没有互相攻击。
注：皇后的攻击范围是一个“米”字，如下图所示：
皇后攻击范围

八皇后问题很容易求解，用一个简单的回溯就可以了。
考虑\(N\)皇后问题，即：

有一个\(N\times N\)的国际象棋棋盘，要在其中摆\(N\)个皇后，求有多少种不同的摆法，使得任意两个皇后之间都没有互相攻击。

此时，还是先用标准的「回溯」算法解决问题：

#include <cstdio>
#define maxn 20
using namespace std;bool row[maxn], diag_left[maxn << 1], diag_right[maxn << 1];
int ans, n;void dfs(int i)
{if(i == n){ans ++;return;}for(int j=0; j<n; j++)if(!row[j] && !diag_left[i + j] && !diag_right[i - j + n]){row[j] = diag_left[i + j] = diag_right[i - j + n] = true;dfs(i + 1);row[j] = diag_left[i + j] = diag_right[i - j + n] = false;}
}int main()
{scanf("%d", &n);ans = 0;dfs(0);printf("%d\n", ans);return 0;
}

代码很移动，也不是重点，这里就不详细解释了。对于\(N=13\)，搜索时间约为\(243\mathrm{ms}\)；\(N=14\)，\(1.31\mathrm s\)；\(N=15\)，\(8.14\mathrm s\)；\(N=16\)…… \(53.4\mathrm s\)。

明显，这样的算法效率太低，我们来考虑使用位运算优化。
首先，我们把上面程序里的row、diag_left和diag_right换成一个int整数，赋值、取值全部改用位运算。但这样对整体的时间优化还是不大，我们要充分发挥位运算的优势——“百发百中”，即利用lowbit算法，确保每次枚举到的都是目前一步可放置的位置，减少不必要的判断。此时，我们改变diag_left和diag_right的含义，使diag_left表示左下-右上的\(45\degree\)对角线上当前一步可放置的皇后位置集合，diag_right同理。见代码：

#include <cstdio>
using namespace std;int ans, mx;void dfs(int row, int diag_left, int diag_right)
{if(row == mx){ans ++;return;}int a = mx & ~(row | diag_left | diag_right);while(a){int p = a & -a; a ^= p;dfs(row | p, (diag_left | p) >> 1, (diag_right | p) << 1);}
}int main()
{int n;scanf("%d", &n);ans = 0;mx = (1 << n) - 1;dfs(0, 0, 0);printf("%d\n", ans);return 0;
}

此时，计算\(16\)皇后只需\(6.23\mathrm s\)！
习题：洛谷 P1092 [NOIP2004 提高组] 虫食算

附：N皇后问题的两种解法耗时对比

本测试中，两种算法耗时均为在Intel i7-12700H CPU上\(5\)次程序运行的最快速度。

\(N\) 无优化 位运算优化 速度提升
\(13\) \(253\mathrm{ms}\) \(66\mathrm{ms}\) \(2.83\text x\)
\(14\) \(1.31\mathrm s\) \(179\mathrm{ms}\) \(6.32\text x\)
\(15\) \(8.14\mathrm s\) \(955\mathrm{ms}\) \(7.52\text x\)
\(16\) \(53.4\mathrm s\) \(6.23\mathrm s\) \(7.57\text x\)

4.3 其他应用

4.3.1 两数交换

void swap(int& a, int& b)
{a ^= b ^= a ^= b;
}

位运算交换法扩展：超快GCD

inline int gcd(int a, int b)
{if(b) while(b ^= a ^= b ^= a %= b);return a;
}

4.3.2 两数平均数（防溢出）

inline int average1(int x, int y)
{return (x >> 1) + (y >> 1) + (x & y & 1);
}inline int average2(int x, int y)
{return (x & y) + ((x ^ y) >> 1);
}

4.3.3 判断一个数是否为\(2\)的整数次幂

inline bool ispowof2(int x)
{return x > 0 && !(x & x - 1);
}

5. 总结

本文详细讲解了位运算的使用和扩展。

创作不易，各位如果觉得好的话就请给个三连，感谢大家的支持！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/794256.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

【算法笔记】【专题】RMQ 问题：ST表/树状数组/线段树

【算法笔记】【专题】RMQ 问题：ST表/树状数组/线段树

0. 前言 好久没更算法笔记专栏了，正好学了新算法来更新…… 这也是本专栏的第一个专题问题，涉及到三种数据结构，如果写得有问题请各位大佬多多指教，谢谢！ 1. 关于 RMQ 问题 RMQ 的全称是 Range Minimum/Maximum Query，即区间最大/最小值问题。 本文中，我们的算法以求最大…
阅读更多...
【算法笔记】树形DP算法总结详解

【算法笔记】树形DP算法总结详解

0. 定义 树形DP，又称树状DP，即在树上进行的DP，是DP（动态规划）算法中较为复杂的一种。 1. 基础 令\(f[u]=~\)与树上顶点\(u\)有关的某些数据，并按照拓扑序（从叶子节点向上到根节点的顺序）进行\(\text{DP}\)，确保在更新一个顶点时其子节点的dp值已经被更新好，以更新当前…
阅读更多...
Seay安装和初步使用

Seay安装和初步使用

作者网站现在已经无法访问：http://www.cnseay.com/2951/， 可以使用这个GitHub - f1tz/cnseay: Seay源代码审计系统 下载完安装包之后，解压到自己想要的电脑路径即可，无需进行任何额外的配置 利用工具对sql注入进行分析 进入软件之后，点击新建项目，选择需要分析的文件(这里…
阅读更多...
纸浆

纸浆

日线： 小时线： 15分钟趋势： 关注5750一线支撑
阅读更多...
代码整洁之道--读书笔记(5)

代码整洁之道--读书笔记(5)

代码整洁之道简介： 本书是编程大师“Bob 大叔”40余年编程生涯的心得体会的总结，讲解要成为真正专业的程序员需要具备什么样的态度，需要遵循什么样的原则，需要采取什么样的行动。作者以自己以及身边的同事走过的弯路、犯过的错误为例，意在为后来者引路，助其职业生涯迈上更…
阅读更多...
02网络参考模型

02网络参考模型

02网络参考模型02网络参考模型常见网络模型因为 OSI协议栈比较复杂 ，且TCP和IP两大协议在业界被广泛使用，所以 TCP/IP参考模型 成为了互联网的主流参考模型。OIS网络模型层级作用7.应用层 应用层 对应用程序提供接口。6.表示层进行数据格式的转换，以确保一个系统生成的应用层…
阅读更多...
《痞子衡嵌入式半月刊》 第 107 期

《痞子衡嵌入式半月刊》 第 107 期

痞子衡嵌入式半月刊： 第 107 期这里分享嵌入式领域有用有趣的项目/工具以及一些热点新闻，农历年分二十四节气，希望在每个交节之日准时发布一期。 本期刊是开源项目（GitHub: JayHeng/pzh-mcu-bi-weekly），欢迎提交 issue，投稿或推荐你知道的嵌入式那些事儿。 上期回顾 ：《…
阅读更多...
鼠标悬停显示的轮播图

鼠标悬停显示的轮播图

今日整理,发现这种轮播图是最难实现的一种, 1.再循环中难以控制单一品类商品显示 解决办法: 在外面的主类里面添加&:hover触发标签属性的更改,这样可以单一作用 2.在循环中触发事件,所有的同一事件都会触发 解决办法:先建立模版控制排版,再从单一内容开始微调 <script s…
阅读更多...
如何把网页的公式优雅地拷贝到word中：数学公式识别神器—Mathpix Snip

如何把网页的公式优雅地拷贝到word中：数学公式识别神器—Mathpix Snip

这个编辑器其实在把chatgpt的公式粘贴到word中时就已经使用了，用的是网页版。 现在下载了软件（但是好像一个月试用期过后得收费？但是就目前来说，体验感真的超级好） 把公式复制粘贴转成mathtype公式 可以截取电脑屏幕上的图像，如果图像上面有公式的话，就会识别，之后可以…
阅读更多...
Redis 入门 - 图形化管理工具如何选择，最全分类

Redis 入门 - 图形化管理工具如何选择，最全分类

Redis图形化管理工具可分为四类：命令行工具、桌面客户端工具、网页工具、插件工具。看看哪一款适合你呢？工欲善其事必先利其器，上一章Redis服务环境已经搭建完成，现在就需要一个趁手的工具，有个好工具可以做到事半功倍。 Redis图形化管理工具五花八门，可供选择的很多，大…
阅读更多...
Javaweb-事务

Javaweb-事务

注意在当前窗口是修改了的：而在其他窗口是不修改的：select @@autocommit;修改为手动提交：
阅读更多...
格路计数

格路计数

前言 完全借鉴于 洛谷日报 前提条件 在一个网格图上, 每一次可以从 \((x,y)\) 走到 \((x+1,y-1)\) 或者 \((x+1,y-1)\) 限制是一条直线 \(y=k\) 题外话 我们其实可以发现这和每一次可以从 \((x,y)\) 走到 \((x+1,y)\) 或者 \((x, y+1)\) 限制是一条 \(45\)的斜线 \(y=x+k\) 是等…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023