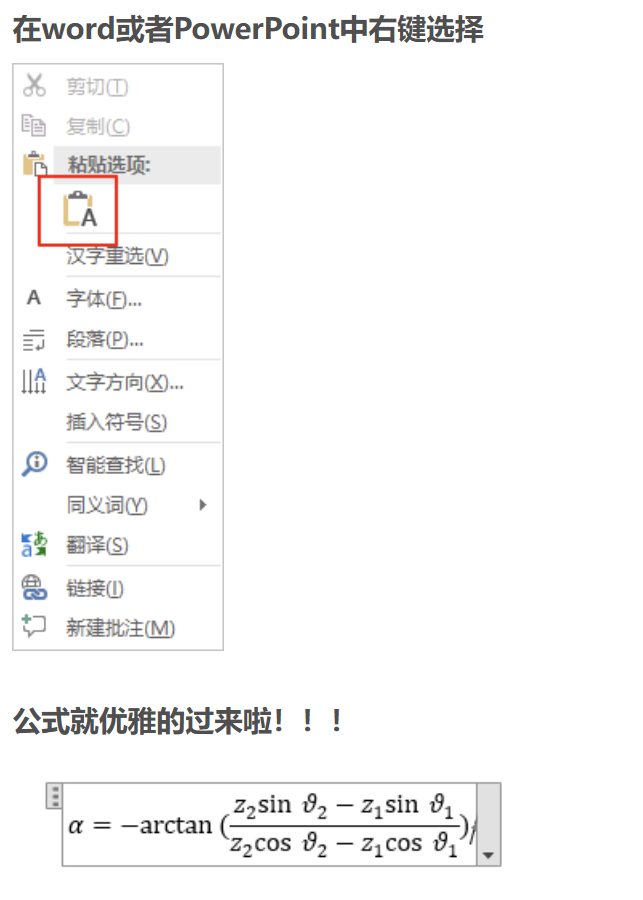
A - Christmas Present
题目大意
给定两个正整数 \(B,G\)(\(1\le B,G\le 1000\) 且 \(B\ne G\)),判断哪个更大。
分析
模拟即可。
代码
#include <cstdio>
using namespace std;int main()
{int b, g;scanf("%d%d", &b, &g);puts(b > g? "Bat": "Glove");return 0;
}
B - Christmas Trees
题目大意
给定 \(A,M,L,R\)。
对于任意整数 \(k\),Snuke 都会在数轴上的 \(A+kM\) 处放置一棵圣诞树。
试问区间 \([L,R]\) 中共有多少棵圣诞树?
\(-10^{18}\le A\le 10^{18}\)
\(1\le M\le 10^9\)
\(-10^{18}\le L\le R\le 10^{18}\)
分析
不难发现,对于任意整数 \(x\),数轴上 \(x\) 处有圣诞树当且仅当 \(x \equiv A \ (\bmod \ M)\)。变形可得 \(x-A \equiv 0 \ (\bmod \ M)\),即 \((x-A) \mid M\)。故只需考虑相对于 \(A\) 的坐标,所以统计 \([L-A,R-A]\) 中 \(M\) 的倍数数量即可。
代码
使用 C++ 语言时,注意正确处理负数的情况。
#include <cstdio>
using namespace std;using LL = long long;int main()
{LL a, l, r;int m;scanf("%lld%d%lld%lld", &a, &m, &l, &r);l -= a, r -= a;if(l < 0) l = -((-l) / m * m);else l = (l + m - 1) / m * m;if(r < 0) r = -((-r + m - 1) / m * m);else r = r / m * m;printf("%lld\n", (r - l) / m + 1);return 0;
}
C - Socks 2
题目大意
有长为 \(2N\) 的序列 \(S=(1,1,2,2,\dots,N,N)\)。
给定 \(A=(A_1,\dots,A_K)\),将 \(S\) 中数字 \(A_1,\dots,A_K\) 各拿掉一个,剩余 \(2N-K\) 个。
对这 \(2N-K\) 个数进行两两组合(可能剩余 \(1\) 个),使得每对数之差的绝对值之和最小。输出这个最小和。
\(1\le K\le N\le 2\times 10^5\)
\(1\le A_1<A_2<\dots<A_K\le N\)
分析
首先,可以证明我们一定会将 \(N-K\) 个成双的数字进行自我组合。
简要证明
采用 反证法。假设有两个 \(a\),我们将它们分别与 \(b,c\) 组合。显然:\[|a-b|+|a-c| \ge |a-a|+|b-c| \]于是,将 \(a,a\) 组合、\(b,c\) 组合的方案一定不比原方案差。因此直接组合 \(a,a\),一定能得到最优解。
由于 \(|a-a|=0\),所以这部分可以直接忽略,将单个的数字,即 \(A_1,\dots,A_K\) 进行组合即可。
分两种情况讨论。
-
\(K\) 为偶数:此时组合没有剩余。不难发现,相邻两两组合即为最优解,所以答案为:
\[\mathrm{ans}=\sum_{i=1}^{k/2} A_{2i}-A_{2i-1} \]直接计算即可。注意 \(A\) 已排序,故无需取绝对值。
-
\(K\) 为奇数:此时组合剩余一个。枚举此剩余的数,从 \(A\) 中删去就转换成了偶数的情况。但是暴力计算的时间复杂度为 \(\mathcal O(K^2)\),维护前缀后缀和即可优化到 \(\mathcal O(K)\)。
综上,我们在 \(\mathcal O(K)\) 的时间内解决了此问题。
代码
#include <cstdio>
#define maxn 200005
using namespace std;inline void setmin(int& x, int y)
{if(y < x) x = y;
}int a[maxn], pre[maxn], suf[maxn];int main()
{int n, k;scanf("%d%d", &n, &k);for(int i=1; i<=k; i++)scanf("%d", a + i);if(!(k & 1)){int ans = 0;for(int i=1; i<=k; i+=2)ans += a[i + 1] - a[i];printf("%d\n", ans);return 0;}for(int i=1; i<k; i+=2)pre[i] = pre[i + 1] = pre[i - 1] + a[i + 1] - a[i];for(int i=k-1; i>0; i-=2)suf[i] = suf[i + 1] = suf[i + 2] + a[i + 1] - a[i];int ans = 1e9;for(int i=1; i<=k; i++){int cur = i & 1? pre[i - 1] + suf[i + 1]: a[i + 1] - a[i - 1] + pre[i - 2] + suf[i + 2];setmin(ans, cur);}printf("%d\n", ans);return 0;
}
D - Reindeer and Sleigh
题目大意
有 \(N\) 个雪橇,编号为 \(1,2,\dots,N\)。拉动第 \(i\) 个雪橇需要 \(R_i\) 只驯鹿。
给定 \(Q\) 次询问,每次给定正整数 \(X\):
- \(X\) 只驯鹿最多能拉动多少个雪橇?
注意:雪橇可以任选,每只驯鹿最多只能拉一个雪橇。
\(1\le N,Q\le 2\times 10^5\)
\(1\le R_i\le 10^9\)
\(1\le X\le 2\times 10^{14}\)
分析
首先,为了拉到最多的雪橇,我们考虑贪心的策略:从 \(R_i\) 最小的雪橇开始拉,从小到大直到驯鹿不够用为止。
因此我们先对 \(R_i\) 进行排序,很明显这不影响结果。此时令前缀和 \(S_i=\sum_{j=1}^i R_j\),则当 \(S_i \le X\) 时,可以拉动前 \(i\) 个雪橇。故只需找到最大的 \(i\) 使得 \(S_i\le X\) 即为所求。此时注意到前缀和已经有序,所以直接在 \(S\) 上使用二分查找即可。
总时间复杂度为 \(\mathcal O(N\log N)\)。
代码
#include <cstdio>
#include <algorithm>
#define maxn 200005
using namespace std;using LL = long long;
LL s[maxn];int main()
{int n, q;scanf("%d%d", &n, &q);for(int i=0; i<n; i++)scanf("%lld", s + i);sort(s, s + n);for(int i=1; i<n; i++)s[i] += s[i - 1];while(q--){LL x;scanf("%lld", &x);printf("%d\n", int(upper_bound(s, s + n, x) - s));}return 0;
}
E - Christmas Color Grid 1
题目大意
有一个 \(H\times W\) 的网格,其中.代表红色,#代表绿色。
随机选一个红色方块,将其涂成绿色。将网格抽象成一张简单无向图,边连接相邻(上下左右)的绿色节点。
图中连通分量个数的期望值是多少?对 \(998244353\) 取模。
\(1\le H,W\le 1000\)
分析
暴力算法的时间复杂度是 \(\mathcal O(H^2W^2)\),显然不满足要求。
考虑将一个红色方块涂成绿色对绿色连通分量数的贡献。令它周围属于不同连通分量的绿色方块个数为 \(n\),则此次操作会将答案减去 \(n-1\)。这样,我们先预处理出连通分量,就可以 \(\mathcal O(1)\) 的计算答案。
此问题可以用 DFS、BFS 或并查集解决。示例代码使用并查集,时间复杂度约为 \(\mathcal O(HW)\)(忽略小函数)。
代码
#include <cstdio>
#include <unordered_map>
#include <set>
#include <atcoder/modint>
#define maxn 1005
using namespace std;using modint = atcoder::modint998244353;int n, m, fa[maxn * maxn];
char s[maxn][maxn];int find(int x) { return fa[x] == x? fa[x]: fa[x] = find(fa[x]); }
inline int calc(int x, int y) { return x * m + y; }
inline int fc(int x, int y) { return find(calc(x, y)); }
inline void merge(int x, int y) { fa[find(x)] = find(y); }int main()
{scanf("%d%d", &n, &m);for(int i=0; i<n; i++)scanf("%s", s[i]);int k = n * m;for(int i=0; i<k; i++)fa[i] = i;for(int i=0; i<n; i++)for(int j=0; j<m; j++){if(s[i][j] != '#') continue;if(i && s[i - 1][j] == '#') merge(calc(i, j), calc(i - 1, j));if(j && s[i][j - 1] == '#') merge(calc(i, j), calc(i, j - 1));}int cnt = 0, tot = 0;for(int i=0; i<n; i++)for(int j=0; j<m; j++)if(s[i][j] == '#' && fc(i, j) == calc(i, j))cnt ++;modint ans = 0;for(int i=0; i<n; i++)for(int j=0; j<m; j++)if(s[i][j] == '.'){set<int> S;if(i && s[i - 1][j] == '#') S.insert(fc(i - 1, j));if(s[i + 1][j] == '#') S.insert(fc(i + 1, j));if(j && s[i][j - 1] == '#') S.insert(fc(i, j - 1));if(s[i][j + 1] == '#') S.insert(fc(i, j + 1));int cur = cnt - (int)S.size() + 1;ans += cur, tot ++;}printf("%d\n", (ans / tot).val());return 0;
}
F - Christmas Present 2
题目大意
圣诞老人 Santa 要在平面直角坐标系中给孩子们送礼物啦!
他的家在 \((S_X,S_Y)\) 处。他要按照数字顺序给 \(N\) 个孩子送出礼物。第 \(i\) 个孩子的家在 \((X_i,Y_i)\) 处。
Santa 手上最多只能一次性拿 \(K\) 个礼物。他想用最短的路程送完所有礼物,再回到自己家,求最短的总路程是多少?
\(1\le K\le N\le 2\times 10^5\)
\(-10^9\le S_X,S_Y,X_i,Y_i \le 10^9\)
\((S_X,S_Y)\ne (X_i,Y_i)\)
\((X_i,Y_i)\ne (X_j,Y_j)\ (i\ne j)\)
分析
这里介绍我自己的独具特(chōu)色(xiàng)的解法,常规解法请参考官方题解。
考虑 dp,令 \(f_{i,j}\) 表示走到第 \(i\) 个房子并送完前 \(i\) 个礼物时,手上剩余 \(j\) 个礼品的最短路程。很显然,我们每次回家都一定拿满 \(K\) 个礼品,则 \(j=k-1\) 一定是拿了礼品之后送出一个。故:
其中 \(d(a,b)\) 表示房子 \(a\) 到 \(b\) 的路程。特别规定 \(0\) 号房子为 \((S_X,S_Y)\),即圣诞老人的住处。这样,答案即为 \(\min f_n+d(n,0)\)。
直接计算的复杂度为 \(\mathcal O(NK)\),时间和空间上都不能接受。
然而,仔细观察递推式可以发现,\(f_i\) 这一行实际上就是由前一行 \(f_{i-1}\) 删去第一个元素,再整体加 \(d(i-1,i)\),并在最后添上 \(f_{i,k-1}\) 得到的。
因此,我们可以用一个deque(双端队列)动态维护状态。对于整体加的操作,用一个变量维护整体的变化值即可。这样空间的问题就得到了解决。再进一步考虑,用一个multiset(可重集合,基于红黑树)或者二叉堆维护队列内元素,求 \(\min\) 的操作时间就减小到了 \(\mathcal O(\log K)\),可以接受。
于是,我们就成功地在 \(\mathcal O(N\log K)\) 的时间和 \(\mathcal O(N+K)\) 的空间内解决了此问题。另外,我们还可以把deque同时充当单调队列,这样时间也优化到了 \(\mathcal O(N+K)\)。两种实现的示例代码都会给出。
代码
实现 1:deque + multiset
#include <cstdio>
#include <deque>
#include <set>
#define maxn 200005
using namespace std;using ld = long double;
const ld INF = 2e18l;int x[maxn], y[maxn];inline ld dis(int i, int j)
{return __builtin_hypotl(x[i] - x[j], y[i] - y[j]);
}int main()
{int n, k;scanf("%d%d", &n, &k);for(int i=0; i<=n; i++)scanf("%d%d", x + i, y + i);deque<ld> f;multiset<ld> s;k --;for(int i=0; i<k; i++)f.push_back(INF), s.insert(INF);f.push_back(dis(0, 1)), s.insert(dis(0, 1));ld dt = 0;for(int i=2; i<=n; i++){ld lt = *s.begin() + dis(i - 1, 0) + dis(0, i) + dt;s.erase(s.find(f.front())), f.pop_front();dt += dis(i - 1, i), lt -= dt;f.push_back(lt), s.insert(lt);}printf("%.15Lf\n", dt + *s.begin() + dis(n, 0));return 0;
}
实现 2:单调队列
#include <cstdio>
#include <deque>
#define maxn 200005
using namespace std;int x[maxn], y[maxn];inline double dis(int i, int j)
{return __builtin_hypotl(x[i] - x[j], y[i] - y[j]);
}int main()
{int n, k;scanf("%d%d", &n, &k);for(int i=0; i<=n; i++)scanf("%d%d", x + i, y + i);deque<pair<double, int>> f;f.emplace_back(dis(0, 1), 1);double dt = 0;for(int i=2; i<=n; i++){double lt = f.front().first + dis(i - 1, 0) + dis(0, i) + dt;if(f.front().second == i - k) f.pop_front();dt += dis(i - 1, i), lt -= dt;while(!f.empty() && f.back().first >= lt) f.pop_back();f.emplace_back(lt, i);}printf("%.15lf\n", dt + f.front().first + dis(n, 0));return 0;
}
G - Christmas Color Grid 2
题目大意
有一个 \(H\times W\) 的网格,其中.代表红色,#代表绿色。
随机选一个绿色方块,将其涂成红色。将网格抽象成一张简单无向图,边连接相邻(上下左右)的绿色节点。
图中连通分量个数的期望值是多少?对 \(998244353\) 取模。
\(1\le H,W\le 1000\)
E 与 G 的区别
- E:将红色涂成绿色。求绿色连通块个数。
- G:将绿色涂成红色。求绿色连通块个数。
分析
注意到本题中红色方块没有任何实质意义,于是先将绿色方块建成一张图。此时题目变为:
- 从简单无向图中随机选取一个结点,将此结点和与其相连的边全部删除。求连通分量个数的期望值,对 \(998244353\) 取模。
根据“删去无向图中一个点导致连通分量个数改变”,很容易联想到割点。对求割点的 Tarjan 算法稍加改编,就可以计算删去一个点能把图分割成的连通块个数。详见代码。
代码
#include <cstdio>
#include <vector>
#include <atcoder/modint>
#define maxn 1000005
using namespace std;using modint = atcoder::modint998244353;inline void setmin(int& x, int y)
{if(y < x) x = y;
}vector<int> G[maxn];inline void add(int x, int y)
{G[x].push_back(y);G[y].push_back(x);
}int root, low[maxn], cnt, dfn[maxn], ncut[maxn];void tarjan(int v)
{low[v] = dfn[v] = ++cnt;ncut[v] = v != root;for(int u: G[v])if(!dfn[u]){tarjan(u);if(low[u] >= dfn[v])ncut[v] ++;setmin(low[v], low[u]);}else setmin(low[v], dfn[u]);
}char s[1005][1005];
int id[1005][1005];int main()
{int n, m;scanf("%d%d", &n, &m);for(int i=1; i<=n; i++)scanf("%s", s[i] + 1);int num = 0;for(int i=1; i<=n; i++)for(int j=1; j<=m; j++)if(s[i][j] == '#'){id[i][j] = ++num;if(s[i - 1][j] == '#') add(num, id[i - 1][j]);if(s[i][j - 1] == '#') add(num, id[i][j - 1]);}int cc = -1;for(int i=1; i<=num; i++)if(!dfn[i])tarjan(root = i), cc ++;modint ans = 0;for(int i=1; i<=num; i++)ans += cc + ncut[i];printf("%d\n", (ans / num).val());return 0;
}
后记
首先预祝大家圣诞节快乐 🎉!这场比赛从标题到题目设定,无不与圣诞节有关,AtCoder 官方算是精心准备了这场圣诞庆祝赛 💝。
遗憾的是我在比赛中先做了 A~E 和 G,F 题比赛结束后 51s 提交,AC。挺可惜的,难得 G 能做出来一次,差点 AK,结果差的就是不到一分钟 😂。希望下次能比得更好,也希望大家能再接再厉。加油!😚