最近开始写 CSP 模拟的题,实际上考的题一点也不 CSP
题意
有一个长度为 \(n\) 的序列 \(A\),\(0\leq A_i<k\),你可以每次选取一个区间,将区间内所有元素 \(+1\),然后将区间内所有元素对 \(k\) 取模。问最少几次操作可以把序列中所有元素都变为 \(0\)。
思路
假设现在有一个数列 \([2,3,1,0,3,2]\),\(k=4\),我们考虑如何将它变为 \(0\)。
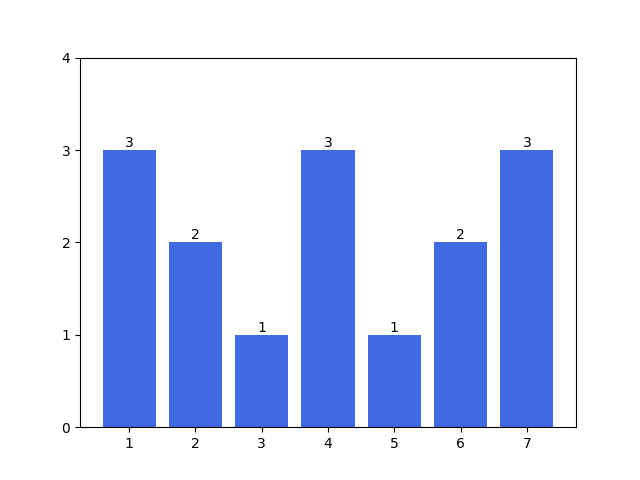
发现每次操作后都要模 \(k\) 的限制非常烦,因此我们做一个转化,每次操作直接加,而“区间内所有元素等于 \(0\)” 转化为了 “区间内所有元素\(\bmod k=0\) ”。
以上图为例,最优的方案为 \((1,7),(2,6),(3,5),(4,4),(4,4)\),共五步,我们把表示“增加值”的序列 \(B\) 用橙色表示。
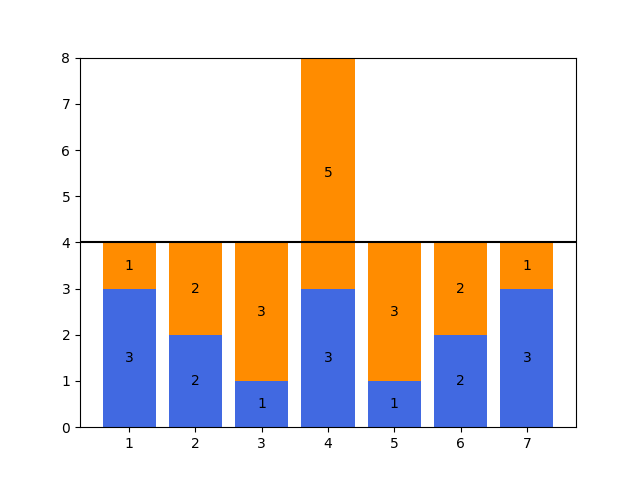
如果把整张图“倒过来”,如下图,我们惊喜地发现这是一个经典问题,求多少次区间加 \(1\) 能覆盖代表 \(B\) 的橙色部分。很显然,操作次数即为 \(B\) 的差分数组 \(B^d\) 中的 \(>0\) 的数之和。
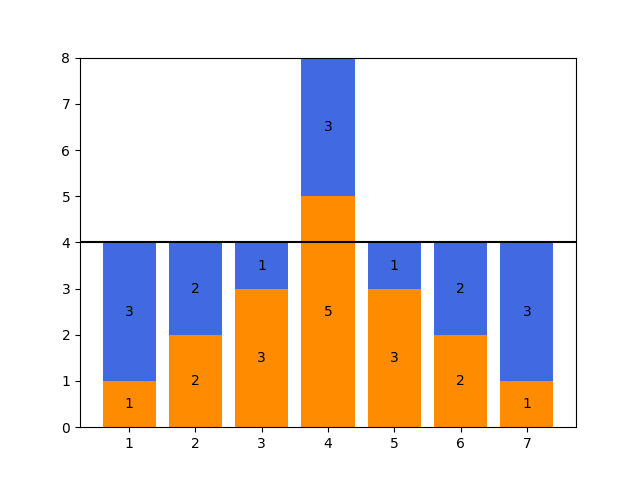
并且我们发现 \(B_i=(k-A_i)+ck\),且 \(c\) 的取值只可能为 \(0\) 或 \(1\) 时才优,为什么?因为考虑初始时差分数组 \(B^d\) 中所有元素绝对值一定是 \(<k\) 的,那么 \(B_i\) 加一次 \(k\) 体现在 \(B^d\) 上便为 \(B^d_i+k,B^d_{i+1}-k\),可以发现此时 \(B^d_i\) 必为正数且 \(B^d_{i+1}\) 必为负数,那么再加由于 \(B^d_{i+1}\) 只会越来越负不计入答案,而 \(B^d_i\) 为正且越来越大,\(B^d\) 的正数和只会更大。
因此我们考虑找到最优的给 \(B_i\) 加 \(k\) 的方案,根据差分数组的性质,若 \(B\) 上有连续的一段区间 \([l,r-1]\) 都被加上 \(k\),则反映到 \(B^d\) 上为 \(B^d_l+k,B^d_r-k\),此时 \(B^d_l\) 必为正数,\(B^d_r\) 必为负数,假设原先 \(B^d_r\) 为正数,那么这个操作对答案的贡献为原先的 \(B^d_r\) 减去现在的 \(B^d_l\)。听到这 solution 大概已经浮出水面了:即遍历差分数组 \(B^d\),对于每个大于 \(0\) 的 \(B^d_i\),找它前面最小的 \(B^d_j\) 判断操作后能不能使得答案变得更小,贪心即可。
注意操作后 \(B^d_i\) 将会变成负数,它也可以和后面的其他 \(B^d_t>0\) 进行一次操作。这有点类似反悔贪心的思想:对于 \(j<i<t\),\(j\) 和 \(i\) 操作,\(i\) 再和 \(t\) 操作实际上等价于 \(j\) 和 \(t\) 操作,\(i\) 就被“反悔”掉了。
代码
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int MAXN=1e7+5;
int n=0,k,a[MAXN],b[MAXN];
string num;
priority_queue<pii,vector<pii>,greater<pii>>pq;
int main(){freopen("modulo.in","r",stdin);freopen("modulo.out","w",stdout);ios::sync_with_stdio(false);cin>>k>>num;a[++n]=num[0]-'0';for(int i=1;i<num.size();i++){if(num[i]!=num[i-1])a[++n]=num[i]-'0';}for(int i=1;i<=n;i++){if(a[i]!=0) a[i]=k-a[i];}for(int i=1;i<=n;i++){b[i]=a[i]-a[i-1];}for(int i=1;i<=n;i++){if(b[i]<0) pq.push(make_pair(b[i],i));else if(b[i]>0){if(pq.empty()) continue;int id=pq.top().second;if(b[id]+k<b[i]){pq.pop();b[id]+=k;b[i]-=k;pq.push(make_pair(b[i],i));}}}int ans=0;for(int i=1;i<=n;i++){if(b[i]>0) ans+=b[i];}cout<<ans<<endl;return 0;
}
后记
CF有道题有点类似,实际上还要简单一点,CF1852C。