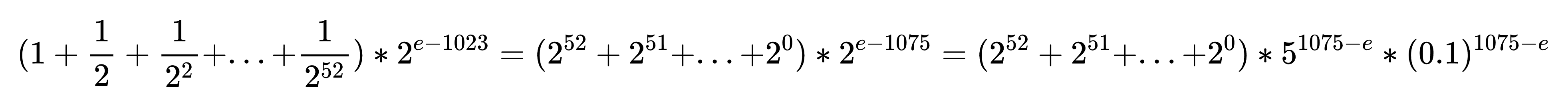Description
一个合法的串定义为:长度在 \([l,r]\) 之间,且只含 0,1,并且不存在连续 \(2\) 个或更多的 \(0\)。
现在要选出 \(k\) 个长度相同的合法的串,问有几种选法,答案模 \(10^9+7\)。
Solution
容易发现答案为 \(\sum_{i=l+2}^{r+2}{\binom{Fib_i}{k}}\)。先将 \(l,r\) 都加 \(2\),题目就转化为了求 \(\sum_{i=l}^{r}{Fib_i^{\underline{k}}}\)。
注意到下降幂是不好做区间求和的,考虑用第一类斯特林数转化为普通幂:
\[x^{\underline{k}}=\sum_{i=0}^{k}{(-1)^{k-i}{k\brack i}x^i}
\]
于是题目相当于是求斐波那契数列的 \(k\) 次区间和。
但是斐波那契数列的 \(k\) 次区间和仍然是无法做的,注意到等比数列是可以求区间和的,所以可以用通项公式将斐波那契数转化成幂次:
\[\begin{aligned}
Fib_i^k&=\left[\left(\frac{1+\sqrt 5}{2}\right)^i-\left(\frac{1-\sqrt 5}{2}\right)^i\right]^k\\
&=\sum_{j=0}^{i}{\binom{i}{j}\left(\frac{1+\sqrt 5}{2}\right)^{ij}\left(\frac{1-\sqrt 5}{2}\right)^{i(k-j)}}\\
&=\sum_{j=0}^{i}{\binom{i}{j}\left[\left(\frac{1+\sqrt 5}{2}\right)^{j}\left(\frac{1-\sqrt 5}{2}\right)^{k-j}\right]^i}
\end{aligned}
\]
这样就可以做了。但是有个问题,就是 \(\sqrt 5\) 在 \(\bmod 10^9+7\) 意义下没有定义,所以需要维护一个形如 \(a+b\sqrt 5\) 的类。
注意等比数列的比为 \(1\) 的情况要特判。
时间复杂度:\(O(k^2\log r)\)。
Code
#include <bits/stdc++.h>#define int int64_tconst int kMaxK = 205, kMod = 1e9 + 7, kInv2 = 500000004, kInv5 = 400000003;int k, l, r;
int C[kMaxK][kMaxK], S[kMaxK][kMaxK], fac[kMaxK], ifac[kMaxK];constexpr int qpow(int bs, int64_t idx = kMod - 2) {int ret = 1;for (; idx; idx >>= 1, bs = (int64_t)bs * bs % kMod)if (idx & 1)ret = (int64_t)ret * bs % kMod;return ret;
}inline int add(int x, int y) { return (x + y >= kMod ? x + y - kMod : x + y); }
inline int sub(int x, int y) { return (x >= y ? x - y : x - y + kMod); }
inline void inc(int &x, int y) { (x += y) >= kMod ? x -= kMod : x; }
inline void dec(int &x, int y) { (x -= y) < 0 ? x += kMod : x; }int getop(int x) { return (~x & 1) ? 1 : (kMod - 1); }struct Node {int a, b; // a + b * sqrt(5)Node(int _a = 0, int _b = 0) : a(_a), b(_b) {}Node inv() {int k = qpow(sub(1ll * a * a % kMod, 5ll * b % kMod * b % kMod));return {1ll * a * k % kMod, 1ll * sub(0, b) * k % kMod};}friend bool operator ==(Node a, Node b) { return a.a == b.a && a.b == b.b; }friend Node operator +(Node a, Node b) { return {add(a.a, b.a), add(a.b, b.b)}; }friend Node operator -(Node a, Node b) { return {sub(a.a, b.a), sub(a.b, b.b)}; }friend Node operator *(Node a, Node b) { return {add(1ll * a.a * b.a % kMod, 5ll * a.b % kMod * b.b % kMod), add(1ll * a.a * b.b % kMod, 1ll * a.b * b.a % kMod)}; }friend Node operator /(Node a, Node b) { return a * b.inv(); }friend Node operator -(Node a) { return {sub(0, a.a), sub(0, a.b)}; }
};Node qpow(Node bs, int idx) {Node ret = {1, 0};for (; idx; idx >>= 1, bs = bs * bs)if (idx & 1)ret = ret * bs;return ret;
}int getsum(int n, int k) {if (!n) return 0;Node ret = {0, 0}, a = {kInv2, kInv2}, b = {kInv2, sub(0, kInv2)};for (int i = 0; i <= k; ++i) {Node bs = qpow(a, i) * qpow(b, k - i), sum = {0, 0};if (bs == (Node){1, 0}) sum = {n % kMod, 0};else sum = (qpow(bs, n + 1) - bs) / (bs - (Node){1, 0});if (~(k - i) & 1) ret = ret + sum * (Node){C[k][i], 0};else ret = ret - sum * (Node){C[k][i], 0};}if (~k & 1) return 1ll * ret.a * qpow(kInv5, k / 2) % kMod;else return 1ll * ret.b * qpow(kInv5, k / 2) % kMod;
}int getsum(int l, int r, int k) {return sub(getsum(r, k), getsum(l - 1, k));
}void prework() {fac[0] = ifac[0] = C[0][0] = S[0][0] = 1, 1;for (int i = 1; i <= 200; ++i) {C[i][0] = 1;fac[i] = 1ll * i * fac[i - 1] % kMod;ifac[i] = qpow(fac[i]);for (int j = 1; j <= i; ++j) {C[i][j] = add(C[i - 1][j - 1], C[i - 1][j]);S[i][j] = add(S[i - 1][j - 1], 1ll * (i - 1) * S[i - 1][j] % kMod);}}
}void dickdreamer() {prework();std::cin >> k >> l >> r;l += 2, r += 2;int ans = 0;for (int i = 0; i <= k; ++i) {inc(ans, 1ll * S[k][i] * getop(k - i) % kMod * getsum(l, r, i) % kMod);}std::cout << 1ll * ans * ifac[k] % kMod << '\n';
}int32_t main() {
#ifdef ORZXKRfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifstd::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);int T = 1;// std::cin >> T;while (T--) dickdreamer();// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";return 0;
}