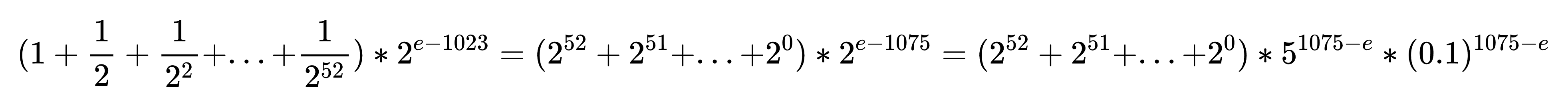题意简述
给你一棵 \(n\) 个节点以 \(1\) 为根的有根树,和一个整数 \(m\)。
对于树上每一个点 \(u\),有三个权值 \(X, Y, Z\)。你需要在 \(u\) 的祖先里(不含 \(u\))中选出至少 \(X\) 个点,记 \(S_1\) 表示这些点到 \(u\) 的距离之和;在 \(u\) 的后代里(不含 \(u\))中选出至少 \(Y\) 个点,记 \(S_2\) 表示这些点到 \(u\) 的距离之和。选出的点数应恰好等于 \(m\)。对于每一个点,求 \(\min \vert S_1 - S_2 + Z \vert\)。如果没有合法的选点方案,输出 \(-1\)。
题目分析
这个距离和不喜欢,拆掉。
为方便叙述,记祖先中选出点集为 \(U\),\(x = \vert U \vert\),同理记后代中选出点集为 \(D\),\(y = \vert D \vert\)。那么:
同理 \(S_2 = -y \operatorname{dpt}(u) + \sum \limits _ {v \in D} \operatorname{dpt}(v)\),那么所求值即为:
发现 \(x + y\) 为一定值 \(m\),故而所求值即为两个 \(\sum\) 与一定值的最少差值绝对值,也就是尽量靠近那个定值。这就来到了此题难点所在。
一个很神的想法是去证明,这两个 \(\sum\) 的和的取值范围为一段连续区间,再扣掉常数个点,这样一个东西。
证明:
显然其有最值。从其取最大值的选点方案,往最小值调整。初始时所有点聚集在下方,取到最大值。
每次我们可以取一个 \(u\),如果 \(\operatorname{fa}(u)\) 没被选,我们就可以让 \(u \gets \operatorname{fa}(u)\),则 \(\operatorname{dpt}(u) \gets \operatorname{dpt}(u) - 1\),就将和往下调整了 \(1\)。
我们还可以让 \(u\) 的一个孩子 \(u\),越过 \(u\),走到 \(\operatorname{fa}(u)\)。但是这样导致将和往下调整了 \(2\)。注意到,我们可以选取另一个点,向下走一步来抵消。如果找不到这一个用来抵消的点,我们的取值范围就被挖去了这一个点。
找不到这样的点,当且仅当所有点都不存在一个没被选择和孩子。情况数不多,大力分讨调整了 \(2\) 后的情形:
- 上方满了,下方为空。
- 上方满了,下方全聚集在底部。
- 上方只有移动的点,下方为空。
- 上方只有移动的点,下方全聚集在底部。
这些局面的 \(\sum + \sum - 1\) 是不能取到的。
那么,我们只需要求出这两个 \(\sum\) 的上下界即可。
对于深度之和的下界,就是尽可能多的点在 \(u\) 的祖先。说明此时有 \(x = x_{\max}\) 个点,深度分别为 \(1, \ldots, x_{\max}\)(\(\operatorname{dpt}(1) = 1\));剩下下方 \(y = m - x_{\max}\) 个点,尽可能靠上贴在 \(u\) 下方。
对于深度之和的上界,同理,尽可能地靠下。上方有 \(x = x_{\min}\) 个点,深度为 \(\operatorname{dpt}(u) - x_{\min}, \ldots, \operatorname{dpt}(u) - 1\);下方 \(y = m - x_{\min}\) 个点,尽可能靠下。
求 \(x_{\min}, x_{\max}\) 是简单的。
对于 \(1 \sim u\) 这条链上的答案很好统计,关键在于子树内,选出 \(k\) 个点,尽可能靠上 / 靠下的深度和。直接上线段树合并维护子树每个深度出现次数,加上前 / 后 \(k\) 大值的和查询。或者树上启发式合并,树状数组上二分。
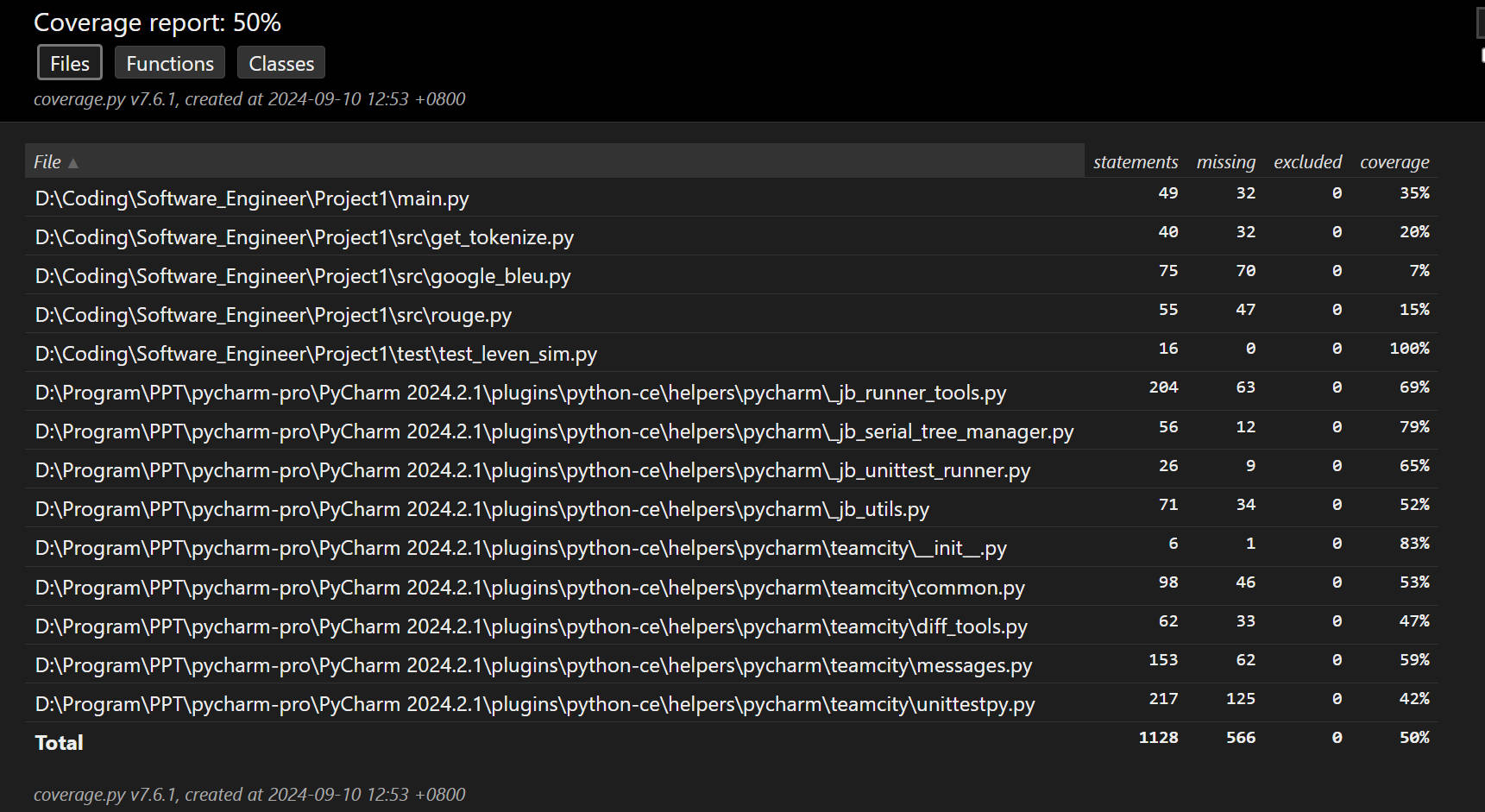
前者是 \(\Theta(n \log n)\) 的。
代码