LOJ4222 「IOI2024」马赛克上色 题解

题目描述

给定长为 \(n\) 、下标从零开始的 \(01\) 序列 \(x,y\) ，保证 \(x_0=y_0\) 。

令 \(col_{0,j}=x_j,col_{i,0}=y_i\) ，对 \(\forall 1\le i\lt n,1\le j\lt n\) ， \(col_{i,j}=[col_{i-1,j}=0\and col_{i,j-1}=0]\) 。

\(q\) 次询问，给定 \(u,d,l,r\) ，求 \(\sum_{i=u}^d\sum_{j=l}^rcol_{i,j}\) 。

数据范围

• \(1\le n,q\le 2\cdot 10^5\) 。
• \(0\le u\lt d\lt n,0\le l\lt r\lt n\) 。

时间限制 \(\texttt{1s}\) ，空间限制 \(\texttt{2048MB}\) 。

分析

先分析 \(col\) 矩阵的性质。

先暴力求出所有满足 \(\min(i,j)\le 2\) 的位置（即前 \(3\) 行 \(3\) 列）的值，容易发现：

• 对于数列 \(col_{n-1,1}\cdots,col_{1,1},col_{1,n-1}\) ，不会有连续两个 \(1\) 。

证明：

显然。

• 对于数列 \(col_{n-1,2},\cdots,col_{2,2},\cdots,col_{2,n-1}\) ，不会有连续两个 \(1\) ，也不会有连续 \(3\) 个 \(0\) 。

证明：

前半部分显然，下面仅考虑后半部分。

若 \(col_{i+1,2}=col_{i,2}=col_{i-1,2}=0\) ，则 \(col_{i+1,1}=col_{i,1}=1\) ，矛盾。

若 \(col_{3,2}=col_{2,2}=col_{2,3}=0\) ，则 \(col_{3,1}=col_{1,3}=1\) ，且 \(col_{2,1}\) 和 \(col_{1,2}\) 至少一个为 \(1\) ，矛盾。

若 \(col_{2,j-1}=col_{2,j}=col_{2,j+1}=0\) ，则 \(col_{1,j}=col_{1,j+1}=1\) ，矛盾。

综上即可得证。

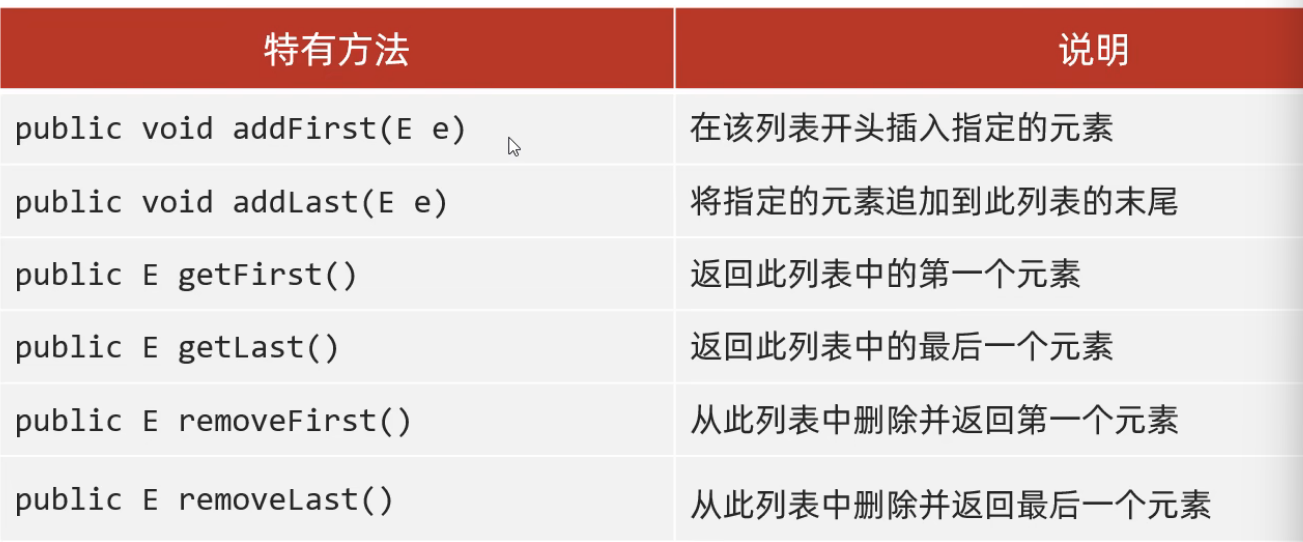
再考虑 \(i\ge 2,j\ge 2\) 时，每个 \(1\) "管辖" 的范围。

它所在斜线一定为 \(1\) ，并且相邻两条斜线一定为 \(0\) ，如下图所示：

通过上述性质我们可以按照斜线不重不漏确定整个矩阵，这是因为两条相邻的斜线 \(1\) 之间只能间隔 \(1\) 或 \(2\) 条斜线 \(0\) 。

---

对询问做二维差分，单独处理前 \(2\) 行 \(2\) 列，转化为求 \(\sum_{i=2}^a\sum_{j=2}^b col_{i,j}\) 。

为方便起见，记 \(m=n-2,a\gets a-1,b\gets b-1\) ，令矩阵下标从 \(1\) 开始。

令 \(o_1,\cdots,o_{2m-1}\) 表示每条斜线的数值，对斜线出发点和穿过询问矩形的边界分类讨论：

• 出发点在左边界，穿过矩形下边界：贡献 \(\sum(a+i-m)\cdot o_i\) 。
• 出发点在左边界，穿过矩形右边界：贡献 \(\sum b\cdot o_i\) 。
• 出发点在上边界，穿过矩形下边界：贡献 \(\sum a\cdot o_i\) 。
• 出发点在上边界，穿过矩形右边界：贡献 \(\sum(b+m-i)\cdot o_i\) 。

预处理 \(\sum o_i\) 和 \(\sum i\cdot o_i\) 即可做到 \(\mathcal O(1)\) 回答，注意经过左上角和右下角的斜线不要算重。

时间复杂度 \(\mathcal O(n+q)\) 。

#include<bits/stdc++.h>
#include"mosaic.h"
#define ll long long
#define vi vector<int>
using namespace std;
const int maxn=2e5+5;
int m;
int o[2*maxn],s1[maxn],s2[maxn],s3[maxn],s4[maxn];
ll t1[2*maxn],t2[2*maxn];
vi col[maxn];
ll get(int l,int r,int x,int y)
{///\sum_{i=l}^r(x+y*i)*o[i]return l<=r?x*(t1[r]-t1[l-1])+y*(t2[r]-t2[l-1]):0;
}
ll calc(int a,int b)
{if(min(a,b)<0) return 0;ll res=0;for(int i=0;i<=1;i++)for(int j=0;j<=1;j++)if(i<=a&&j<=b) res+=col[i][j];if(a>=0) res+=s1[b];if(a>=1) res+=s2[b];if(b>=0) res+=s3[a];if(b>=1) res+=s4[a];if(--a>=1&&--b>=1){res+=get(m+1-a,min(m,b-a+m),a-m,1);res+=get(b-a+m+1,m,b,0);res+=get(m+1,b-a+m,a,0);res+=get(max(m+1,b-a+m+1),m+b-1,b+m,-1);}return res;
}
vector<ll> mosaic(vi x,vi y,vi u,vi d,vi l,vi r)
{int n=x.size(),q=u.size();for(int i=0;i<n;i++){col[i].resize(i<3?n:3);for(int j=0;j<col[i].size();j++){if(!i) col[i][j]=x[j];else if(!j) col[i][j]=y[i];else col[i][j]=!col[i-1][j]&!col[i][j-1];}}for(int i=2;i<n;i++) s1[i]=s1[i-1]+col[0][i],s2[i]=s2[i-1]+col[1][i];for(int j=2;j<n;j++) s3[j]=s3[j-1]+col[j][0],s4[j]=s4[j-1]+col[j][1];m=n-2;for(int j=1;j<=2*m-1;j++){o[j]=j<=m?col[m+2-j][2]:col[2][j-m+2];t1[j]=t1[j-1]+o[j],t2[j]=t2[j-1]+o[j]*j;}vector<ll> vec(q);for(int i=0;i<q;i++)vec[i]=calc(d[i],r[i])-calc(u[i]-1,r[i])-calc(d[i],l[i]-1)+calc(u[i]-1,l[i]-1);return vec;
}