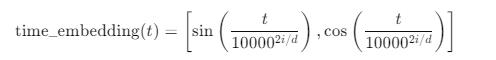
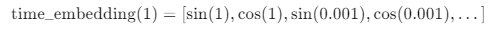
左边的公式和 time_embedding(1) 的区别在于它们表示的维度不同。公式中的左边部分是一个概括性公式,用来说明如何为每个时间步 ( t ) 生成时间嵌入。而具体的 time_embedding(1) 展示的是当 ( t = 1 ) 时,如何生成一个更长维度的时间嵌入向量。
1. 左边公式的含义:
左边的公式表示的是时间步 ( t ) 在不同维度上生成的正弦和余弦值。它用到了参数 ( i ) 和 ( d ),其中:
- ( i ) 是当前的维度索引(不同的 ( i ) 值代表不同的维度),
- ( d ) 是总的嵌入维度。
公式实际上表示,对于嵌入维度的每一个索引 ( i ),我们分别生成正弦和余弦值。这个公式表达了时间步 ( t ) 在不同的维度上如何映射到正弦和余弦值。
2. time_embedding(1) 的具体表示:
time_embedding(1) 展示了当 ( t = 1 ) 时,具体的时间嵌入向量是什么样的。因为时间嵌入是通过正弦和余弦函数生成的,所以它会在嵌入维度的每个索引 ( i ) 上生成两个值:一个是正弦值,另一个是余弦值。
- 对于 ( i = 0 ),我们计算 $ \sin(1) ) 和 ( \cos(1) $,它们是第一个维度的正弦和余弦表示。
- 对于 ( i = 1 ),我们计算 $ \sin\left(\frac{1}{10000^{2 \cdot 1/d}}\right) ) 和 ( \cos\left(\frac{1}{10000^{2 \cdot 1/d}}\right) $,这是第二个维度的正弦和余弦表示。
如此类推,我们继续为后续维度生成对应的正弦和余弦值。每个维度 ( i ) 都会生成一对正弦和余弦值,因此时间嵌入的维度将会是总维度 ( d ) 的两倍。
3. 时间嵌入的维度解释:
具体来说,如果时间嵌入的总维度是 ( d ),那么它将包含 ( d/2 ) 对正弦和余弦值。例如,如果我们生成 6 维的时间嵌入,那么:
\(
\text{time_embedding}(1) = \left[ \sin(1), \cos(1), \sin\left(\frac{1}{10000^{2 \cdot 1 / 6}}\right), \cos\left(\frac{1}{10000^{2 \cdot 1 / 6}}\right), \dots \right]
\)
总共会包含 6 个元素,即 3 对正弦和余弦值。
总结:
左边的公式是一个概括的生成时间嵌入的方式,而右边展示的是一个具体例子,当时间步 ( t = 1 ) 时,如何生成多对正弦和余弦值。每一对正弦和余弦值都对应着嵌入向量的一个维度,因此最终生成的时间嵌入向量的长度是总维度的两倍。