高代丘维声

高代丘维声

线性方程组

线性方程组的消元法

含\(n\)个未知量的线性方程组称为\(n\)元线性方程组，它的一般形式是

\[\left\{\begin{aligned}&a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\ &a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\ &\vdots\\ &a_{s1}x_1+a_{s2}x_2+\cdots+a_{sn}x_n=b_s \end{aligned}\right. \]

如果 \(x_1,x_2,\cdotp\cdotp\cdotp,x_n\) 分别用数 \(c_1,c_2,\cdotp\cdotp\cdotp,c_n\) 代人后, 每个方程都变成恒等式, 那么称 \(n\) 元有序数组 \((c_1,c_2,\cdots,c_n)^{\prime}\) 是线性方程组的一个解, 所有解组成的集合称为这个方程组的解集.

为了书写简便, 将方程组的系数和常数项排成一张表, 这张表称为增广矩阵, 只列出系数则得到系数矩阵.

定义 1.1.1: 由 \(s\times m\) 个数排成的数表称为 \(s\times m\) 矩阵.

例 1.1.2: 解线性方程组

​​​​

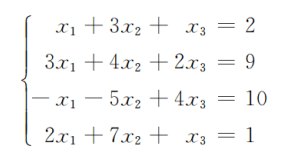
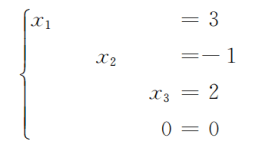
1. 在上述过程中, 对增广矩阵进行了三种变换:

   (1) 把一行的倍数加到另一行上;

   (2) 交换两行;

   (3) 用非零数乘某一行.

   这三种变换成为矩阵的初等行变换​.

2. 增广矩阵经过初等行变换化成了

   \[\begin{bmatrix}1&3&1&2\\0&1&-1&-3\\0&0&3&6\\0&0&0&0\end{bmatrix} \]

   这称为阶梯形矩阵, 其特点是:

   (1) 元素全为 0 的行在下方;

   (2) 元素不全为 0 的行, 其第一个不为 0 的元素称为主元, 主元的列指标随行指标严格递增.

3. 阶梯形矩阵进一步化为

   \[\begin{bmatrix}1&0&0&3\\0&1&0&-1\\0&0&1&2\\0&0&0&0\end{bmatrix} \]

   这称为简化行阶梯型矩阵, 其特点是:

   (1) 非零行的主元都是 1;

   (2) 每个主元所在列的其他元素都是 0.

定理 1.1.1: 任意矩阵都可经过初等行变换化成阶梯形矩阵.

设矩阵为 \(s\times m\) 矩阵, 当 \(s=1\) 时, 显然是阶梯形矩阵. 设 \(s-1\) 行的矩阵可以化为阶梯形, 对 \(s\) 行的矩阵, 不妨设 \(a_{11}\neq0\), 把第一行乘以 \(-\dfrac{a_{i1}}{a_{11}}\) 加到第 \(i\) 行, 得到

\[\begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ 0\\ \vdots&&\bm J_{s-1}\\ 0 \end{pmatrix} \]

由归纳法得证.

推论 1.1.1: 任意矩阵都可经过初等行变换化成简化行阶梯形矩阵.

化简方程组 \(\begin{cases}x_1-x_2+x_3=1\\x_1-x_2-x_3=3\\2x_1-2x_2-x_3=5\end{cases}\) 为 \(\begin{cases}x_1=x_2+2\\x_3=-1\end{cases}\),

若方程组的一部分变量可以用其余变量的至多一次式来表示, 则称这个表达式为一般解.

把 \(n\) 元方程组的增广矩阵化为阶梯形矩阵 \(\bm J\), 若 \(\bm J\) 有 \(r\) 个非零行, 则 \(\bm J\) 有 \(r\) 个主元, 以主元为系数的变量为主变量, 其余为自由变量. 进一步化成简化行阶梯形矩阵 \(\bm J_q\), 则立刻得到一般解的表达式.

线性方程组解的情况及其判别准则

由于经过初等行变换的方程组与原方程组同解, 这里只讨论阶梯形矩阵.

设 \(n\) 元方程组的阶梯形增广矩阵 \(\bm J\) 有 \(r\) 个非零行, \(\bm J\) 有 \(n+1\) 列.

定理 1.2.1:

1. 阶梯形方程组中出现 \(0=d\), 则方程组无解.

2. 阶梯形方程组中没有 \(0=d\), 此时主元的列指标 \(r\leq j_r\leq n\).

   1. 若 \(r=n\), 此时简化行阶梯形矩阵 \(\bm J_q\) 有 \(n\) 个主元, 方程组有唯一解.
   2. 若 \(r<n\), 此时 \(\bm J_q\) 有 \(n-r\) 个自由变量, 方程组有无穷解.

常数项全为 0 的方程组称为齐次线性方程组.

推论 1.2.1: \(n\) 元齐次线性方程组有非零解的充要条件是 \(r<n\).

推论 1.2.2: 若 \(n\) 元齐次线性方程组的方程数 \(s<n\), 则必有非零解.

数域

定义 1.3.1: 复数集的一个子集 \(K\) 如果满足:

1. \(0,1\in K\).
2. \(a,b\in K \Longrightarrow a\pm b\in K, \: ab\in K\), 且 \(b\neq 0\) 时 \(\dfrac{a}{b}\in K\).

则称 \(K\) 是一个数域.

\(0\in K\) 可以略去, 因为 \(0=1-1\in K\). 有理数集 \(\mathbb{Q}\), 实数集 \(\R\), 复数集 \(\mathbb{C}\) 都是数域.

命题 1.3.1: 任何数域都包含 \(\mathbb Q\), 即 \(\mathbb Q\) 是最小的数域.

设 \(K\) 是数域, 则 \(0,1\in K\), 从而 \(2\in K,\cdots, n\in K\) 即 \(\N\sub K\). 同时 \(-n=0-n\in K\), 故 \(Z\sub K\).

最后任意分数 \(\dfrac{a}{b}\in K\), 即 \(\mathbb Q\sub K\).

讨论线性方程组都是在一个给定数域 \(K\) 内讨论, 即系数和常数项都属于 \(K\), 且它的解是 \(K\) 中的数组成的有系数组.

例 1.3.1: 令 \(\bm Q(\sqrt 2)=\{a+b\sqrt 2:a,b\in\mathbb Q\}\), 证明 \(\bm Q(\sqrt 2)\) 是数域.

\(0=0+0\sqrt 2\in \bm Q(\sqrt2)\), \(1=1+0\sqrt2\in \bm Q(\sqrt2)\).

\((a+b\sqrt2)\pm (c+d\sqrt2)=(a+b)+(c+d)\sqrt2\in\bm Q(\sqrt2)\),

\((a+b\sqrt2)(c+d\sqrt2)=(ac+2bd)+(ad+bc)\sqrt2\in\bm Q(\sqrt2)\),

若 \(c,d\neq0\), 则 \(\dfrac{a+b\sqrt2}{c+d\sqrt2}=\dfrac{ac-2bd}{c^2-2d^2}+\dfrac{bc-ad}{c^2-2d^2}\sqrt2 \in\bm Q(\sqrt2)\).

例 1.3.2: \(\displaystyle E=\Big\{ \frac{a_0+a_1\pi}{b_0+b_1\pi}:a_0,a_1,b_0,b_1\in \Z\Big\}\) 是数域吗?

\(\displaystyle \frac1\pi+\frac{1}{1+\pi}=\frac{2+\pi}{\pi+\pi^2}\notin E\), 不是数域.

若 \(\displaystyle E=\Big\{ \frac{P(\pi)}{Q(\pi)}:P,Q为整多项式\Big\}\), 则 \(E\) 成为数域.

行列式

考虑一个二元线性方程组, 其增广矩阵可化为

\[\begin{pmatrix} a_{11}&a_{12}&b_1\\ a_{21}&a_{22}&b_2 \end{pmatrix}\Longrightarrow \begin{pmatrix} a_{11}&a_{12}&b_1\\ 0&a_{22}-\frac{a_{21}}{a_{11}}a_{22}&b_2-\frac{a_{21}}{a_{11}}b_1 \end{pmatrix} \]

若 \(a_{22}-\dfrac{a_{21}}{a_{11}}a_{22}\neq0\), 则方程组有唯一解, 否则有无穷解或无解. 二元方程组有解的充要条件是 \(|\bm A|\neq0\).

n 元排列

\(n\) 个不同正整数的一个全排列称为一个 \(n\) 元排列.

在 \(n\) 元排列 \(a_1,\cdots,a_n\) 中, 任取一对数 \(a_i,a_j\:(i<j)\), 若 \(a_i<a_j\), 则这对数构成一个顺序, 否则构成一个逆序. 一个 \(n\) 元排列中逆序的总数称为逆序数, 记作 \(r(a_1a_2\cdots a_n)\).

逆序数为奇数的排列称为奇排列, 逆序数为偶数称为偶排列.

如 4 元排列 \(2143\), 构成逆序的数对有 \(21,43\), 故 \(r(2143)=2\).

将某一对数互换, 这种变换称为对换.

定理 2.1.1: 对换改变排列的奇偶性.

对换的两数 \(a_i,a_j\) 相邻时, 只有 \(a_i,a_j\) 的逆序数改变, 故奇偶性改变.

一般情形下, \(a_i,a_j\) 对换可以通过以下对相邻数的对换实现:

\[(a_i,a_{i+1}),\cdots,(a_i,a_{j-1}),(a_i,a_j);(a_{j-1},a_j),(a_{j-2},a_j),\cdots,(a_{i+1},a_j) \]

一共 \(2s+1\) 此对换, 故奇偶性改变.

定理 2.1.2: 任一 \(n\) 元排列可以通过对换变为 \(12\cdots n\), 对换次数的奇偶性与该排列的奇偶性相同.

\(12\cdots n\) 是偶排列, 若某一 \(n\) 元排列是奇排列, 则必须经过奇数次对换才能变成偶排列, 另一情况同理.

例 2.1.2: 求 \(n(n-1)\cdots 21\) 的逆序数, 讨论其奇偶性.

该排列中任一数与其右边的数都构成逆序, 故

\[r[n(n-1)\cdots 21]=(n-1)+\cdots+1=\frac{n(n-1)}{2} \]

当 \(n=4k,4k+1\) 时是偶排列, 当 \(n=4k+2,4k+3\) 时是奇排列.

例 2.1.3: 若 \(j_1j_2\cdots j_n\) 的逆序数为 \(r\), 求 \(j_nj_{n-1}\cdots j_1\) 的逆序数.

\(j_1j_2\cdots j_n\) 中共有 \({n\choose 2}\) 对数, 其中构成逆序的有 \(r\) 对.

在原来的 \(j_1j_2\cdots j_n\) 中构成顺序的数对 \(j_t,j_s\), 在 \(j_nj_{n-1}\cdots j_1\) 构成逆序, 故 \(r(j_nj_{n-1}\cdots j_1)={n\choose2}-r\).

例 2.1.4: 由 \(1,2,\cdots,n\) 构成的排列 \(a_1a_2\cdots a_kb_1\cdots b_{n-k}\), 其中 \(a_1<\cdots<a_k\), \(b_1<\cdots<b_{n-k}\), 求该排列的逆序数.

在 \(a_1\) 右边比 \(a_1\) 小的数有 \(a_1-1\) 个, 在 \(a_2\) 右边比 \(a_2\) 小的数有 \(a_2-2\) 个(因为 \(a_1<a_2\)), 在 \(a_k\) 右边比 \(a_k\) 小的数有 \(a_k-k\) 个, 而 \(b_1b_2\cdots b_{n-k}\) 中没有逆序, 故

\[r(a_1a_2\cdots a_kb_1\cdots b_{n-k})=\sum_{i=1}^k (a_i-i)=\sum_{i=1}^n a_i-\frac{k(k+1)}{2} \]

例 2.1.5: 设排列 \(c_1c_2\cdots c_kd_1\cdots d_{n-k}\) 由 \(1,2,\cdots,n\) 构成, 证明

\[(-1)^{r(c_1\cdots c_kd_1\cdots d_{n-k})}=(-1)^{r(c_1\cdots c_k)+r(d_1\cdots d_{n-k})+\sum_{i=1}^k c_i+\frac{k(k+1)}{2}} \]

将 \(c_1\cdots c_k\) 经过 \(s\) 次对换变为 \(a_1\cdots a_n\), 其中 \(a_1<\cdots<a_k\), 则 \((-1)^{r(c_1\cdots c_n)}=(-1)^s\). 于是

\[\begin{aligned} (-1)^{r(c_1\cdots c_kd_1\cdots d_{n-k})}&=(-1)^s(-1)^{r(a_1\cdots a_kd_1\cdots d_{n-k})}\\ &=(-1)^{r(c_1\cdots c_n)} (-1)^{\sum_{i=1}^n a_i-\frac{k(k+1)}{2}+r(d_1\cdots d_n)}\\ &=(-1)^{r(c_1\cdots c_k)+r(d_1\cdots d_{n-k})+\sum_{i=1}^k c_i+\frac{k(k+1)}{2}} \end{aligned} \]

例 2.1.6: 证明全部 \(n\) 元排列中, 奇偶排列各占一半.

设奇排列的集合为 \(A_n\), 偶排列的集合为 \(B_n\). 定义映射 \(f:对换(1,2)\), 则这个映射定义了一种 \(A_n\) 和 \(B_n\) 中的一一对应关系, 故 \(|A_n|=|B_n|\).

n 阶行列式的定义

定义 2.2.1: 设 \(S_n\) 为所有 \(n\) 元排列的集合, 则 \(n\) 阶行列式定义为

\[\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}= \sum_{j_1\cdots j_n\in S_n} (-1)^{r(j_1\cdots j_n)} a_{1j_1} \cdots a_{n j_n} \]

\[\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} \]

​​

行列式的每一项是位于不同行, 不同列元素的乘积, 故只要某行或某列中有一个 0,此项就为 0.

主对角线下方元素都为 0 的行列式称为上三角行列式,

命题 2.2.1:

\[\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1,n-1}& a_{1n}\\ 0 & a_{22} & \cdots & a_{2,n-1} & a_{2n}\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 &\cdots & a_{n-1,n-1} & a_{n-1,n}\\ 0 & 0 & \cdots & 0 & a_{nn} \end{vmatrix}=a_{11}a_{22}\cdots a_{nn} \]

考虑其中的某项 \((-1)^{r(j_1\cdots j_n)} a_{1j_1} \cdots a_{n j_n}\), 要使其不为 0, 则 \(j_n=n\), 而 \(j_{n-1}=n-1\), 以此类推 \(j_k=k\), 故

\[|\bm A|=(-1)^{r(12\cdots n)} a_{11}\cdots a_{nn}=a_{11}\cdots a_{nn} \]

命题 2.2.2: 任意给定行指标的排列 \(i_1\cdots i_n\), 行列式为

\[|\bm A|=\sum_{k_1\cdots k_n\in S_n} (-1)^{r(i_1\cdots i_n)+r(k_1\cdots k_n)}a_{i_1k_1}\cdots a_{i_nk_n} \]

或者给定列指标的排列 \(k_1\cdots k_n\),

\[|\bm A|=\sum_{i_1\cdots i_n\in S_n} (-1)^{r(i_1\cdots i_n)+r(k_1\cdots k_n)}a_{i_1k_1}\cdots a_{i_nk_n} \]

\(n\) 阶行列式的每一项 \((-1)^{r(j_1\cdots j_n)} a_{1j_1} \cdots a_{n j_n}\) 可以写成 \((-1)^{r(i_1\cdots i_n)+r(k_1\cdots k_n)}a_{i_1k_1} \cdots a_{i_nk_n}\), 因为:

设 \(a_{1j_1} \cdots a_{n j_n}\) 经过 \(s\) 此对换变为 \(a_{i_1k_1} \cdots a_{i_nk_n}\), 则

\[(-1)^{r(i_1\cdots i_n)}=(-1)^s,\quad (-1)^{r(k_1\cdots k_n)}=(-1)^{r(j_1\cdots j_n)+s} \]

于是

\[(-1)^{r(i_1\cdots i_n)+r(k_1\cdots k_n)}a_{i_1k_1}\cdots a_{i_nk_n}=(-1)^{r(j_1\cdots j_n)}a_{1j_1}\cdots a_{nj_n} \]

例 2.2.1:

\[\begin{vmatrix}0&a_1&0&\cdots&0\\0&0&a_2&\cdots&0\\ \vdots&\vdots&\vdots&&\vdots\\0&0&0&\cdots&a_{n-1}\\a_n&0&0&\cdots&0\end{vmatrix} \]

其展开式中, 不为 0 的项只有 \((-1)^{r(23\cdots n1)}a_1a_2\cdots a_n=(-1)^{n-1} a_1a_2\cdots a_n\).

例 2.2.2:

\[\begin{vmatrix}0&0&\cdots&0&a_1\\0&0&\cdots&a_2&0\\ \vdots&\vdots&&\vdots&\vdots\\0&a_{n-1}&\cdots&0&0\\a_n&0&\cdots&0&0\end{vmatrix}=(-1)^{r(n\cdots 1)}a_1\cdots a_n=(-1)^{\frac{n(n-1)}{2}} a_1\cdots a_n \]

例 2.2.3:

\[\begin{vmatrix}a_1&a_2&a_3&a_4&a_5\\b_1&b_2&b_3&b_4&b_5\\0&0&0&c_1&c_2\\0&0&0&d_1&d_2\\0&0&0&e_1&e_2\end{vmatrix}=0 \]

该行列式中每一项都包含后三行中位于不同列的元素, 因而必然为 0.

例 2.2.4: 求该行列式的最高次数, 并求 \(x^4\) 和 \(x^3\) 的系数

\[\begin{vmatrix}7x&x&1&2x\\1&x&5&-1\\4&3&x&1\\2&-1&1&x\end{vmatrix} \]

最高为四次. 四次项为 \((-1)^{r(1234)} 7x^4=7x^4\). 三次项为 \((-1)^{r(2134)}x^3+(-1)^{r(4231)}4x^3=-5x^3\).

例 2.2.5: 证明在 \(n\) 阶行列式中, 若第 \(i_1,i_2,\cdots, i_k\) 行分别与第 \(j_1,j_2,\cdots,j_l\) 列交叉位置的元素都是 0, 且 \(k+l>n\), 那么行列式为 0.

行列式的展开式中, 每一项都包含第 \(i_1,\cdots,i_k\) 中位于不同列的元素, 共 \(k\) 个. 而第 \(i_1,\cdots,i_k\) 中只有 \(n-l\) 列的交叉位置的元素可能不为 0, 由于 \(k>n-l\), 故行列式为 0.

习题 2.2.6: 证明若 \(n\geq2\) 阶矩阵 \(\bm A\) 的元素都是 1 或 -1, 则 \(|\bm A|\) 为偶数.

\(|\bm A|\) 的每一项都为 1 或 -1, 设有 \(k\) 项为 1, 则有 \(n!-k\) 项为 -1, 故 \(|\bm A|=2k-n!\) 为偶数.

行列式的性质

性质 1: 转置后, 行列式的值不变.

\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix} =\sum_{i_1\cdots i_n} (-1)^{r(i_1\cdots r_n)} a_{1i_1}\cdots a_{ni_n}= \begin{vmatrix}a_{11}&a_{21}&\cdots&a_{n1}\\a_{12}&a_{22}&\cdots&a_{n2}\\ \vdots&\vdots&&\vdots\\a_{1n}&a_{2n}&\cdots&a_{nn}\end{vmatrix} \]

性质 2: 行列式一行的公因子可以提出来, 即

\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\ka_{i1}&ka_{i2}&\cdots&ka_{in}\\ \vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{m}\end{vmatrix}=k\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\a_{i1}&a_{i2}&\cdots&a_{in}\\ \vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{m}\end{vmatrix} \]

证明: \(左边=\sum_{j_1\cdots j_n}(-1)^{\tau(j_{1}\ldots j_{n})}a_{1j_{1}}\cdots(ka_{ij_{i}})\cdots a_{nj_n}=k\sum_{j_1\cdots j_n}(-1)^{\tau(j_{1}\ldots j_{n})}a_{1j_{1}}\cdots a_{nj_n}=右边\).

性质 3:

\[\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\b_1+c_1&b_2+c_2&\cdots&b_n+c_n\\ \vdots&\vdots&&\vdots\\a_{r1}&a_{r2}&...&a_{rn}\end{vmatrix}=\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\b_1&b_2&\cdots&b_n\\ \vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix}+\begin{vmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\ \vdots&\vdots&&\vdots\\c_1&c_2&\cdots&c_n\\ \vdots&\vdots&&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{vmatrix} \]

证明: \(左边=\sum_{j_1\cdots j_n}(-1)^{\tau(j_{1}\ldots j_{n})}a_{1j_{1}}\cdots(b_{ij_{i}}+c_{ij_i})\cdots a_{nj_n}\\ \qquad\qquad=\sum_{j_1\cdots j_n}(-1)^{\tau(j_{1}\ldots j_{n})}a_{1j_{1}}\cdots b_{ij_{i}}\cdots a_{nj_n}+\sum_{j_1\cdots j_n}(-1)^{\tau(j_{1}\ldots j_{n})}a_{1j_{1}}\cdots c_{ij_i}\cdots a_{nj_n}=右边\).

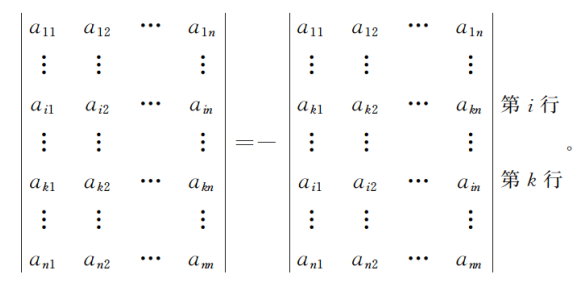
性质 4: 两行互换, 行列式反号.

​​

\[\begin{aligned} 右边&=-\sum_{j_1\cdots j_i\cdots j_k\cdots j_n}(-1)^{r(j_1\cdots j_i\cdots j_k\cdots j_n)} a_{1j_1}\cdots a_{kj_i}\cdots a_{ij_k} \cdots a_{nj_n}\\ &=\sum_{j_1\cdots j_k\cdots j_i\cdots j_n} (-1)^{r(j_1\cdots j_k\cdots j_i\cdots j_n)} a_{1j_1}\cdots a_{ij_k}\cdots a_{kj_i} \cdots a_{nj_n}=左边\\ \end{aligned} \]

性质 5: 两行相同, 则行列式的值为 0.

证明: 依性质 4 交换相同的两行, 得 \(|\bm A|=-|\bm A|\).

性质 6: 两行成比例, 则行列式的值为 0.

性质 7: 把一行的倍数加到另一行上, 行列式的值不变.

证明: 由性质 3 和性质 6 可得.

例 2.3.2:

\[\begin{aligned} \begin{vmatrix}k&\lambda&\lambda&\cdots&\lambda\\ \lambda&k&\lambda&\cdots&\lambda\\ \vdots&\vdots&\vdots&&\vdots\\ \lambda&\lambda&\lambda&\cdots&k\end{vmatrix}= \begin{vmatrix}k+(n-1)\lambda&\lambda&\lambda&\cdots&\lambda\\ k+(n-1)\lambda&k&\lambda&\cdots&\lambda\\ \vdots&\vdots&\vdots&&\vdots\\ k+(n-1)\lambda&\lambda&\lambda&\cdots&k\end{vmatrix} &=[k+(n-1)\lambda] \begin{vmatrix}1&\lambda&\lambda&\cdots&\lambda\\ 0&k-\lambda&\lambda&\cdots&\lambda\\ \vdots&\vdots&\vdots&&\vdots\\ 0&0&0&\cdots&k-\lambda\end{vmatrix}\\ &=[k+(n-1)\lambda](k-\lambda)^{n-1}\end{aligned} \]

例 2.3.4:

\[\begin{aligned} \begin{vmatrix}x_{1}-a_{1}&x_{2}&x_{3}&\cdots&x_{n}\\ x_{1}&x_{2}-a_{2}&x_{3}&\cdots&x_{n}\\ x_{1}&x_{2}&x_{3}-a_{3}&\cdots&x_{n}\\ \vdots&\vdots&\vdots&&\vdots\\ x_{1}&x_{2}&x_{3}&\cdots&x_{n}-a_{n}\end{vmatrix}&=\begin{vmatrix}x_{1}-a_{1}&x_{2}&x_{3}&\cdots&x_{n}\\ a_{1}&-a_{2}&0&\cdots&0\\ a_{1}&0&-a_{3}&\cdots&0\\ \vdots&\vdots&\vdots&&\vdots\\ a_{1}&0&0&\cdots&-a_{n}\end{vmatrix}\\&=a_1\cdots a_n\begin{vmatrix}\frac{x_1}{a_1}-1&\frac{x_2}{a_2}&\frac{x_3}{a_3}&\cdots&\frac{x_n}{a_n}\\ 1&-1&0&\cdots&0\\ 1&0&-1&\cdots&0\\ \vdots&\vdots&\vdots&&\vdots\\ 1&0&0&\cdots&-1\end{vmatrix}\\&=a_1\cdots a_n\begin{vmatrix}\sum_{i=1}^n\frac{x_i}{a_i}-1&\frac{x_2}{a_2}&\frac{x_3}{a_3}&\cdots&\frac{x_n}{a_n}\\ 0&-1&0&\cdots&0\\ 0&0&-1&\cdots&0\\ \vdots&\vdots&\vdots&&\vdots\\ 0&0&0&\cdots&-1\end{vmatrix}\\&=(-1)^{n-1}a_1\cdots a_n\Big( \sum_{i=1}^n \frac{x_i}{a_i}-1\Big) \end{aligned} \]

行列式按行(列)展开

定义 2.4.1: \(n\) 阶矩阵 \(\bm A\) 划去第 \(i\) 行和第 \(j\) 列, 剩余元素按原来次序组成的 \(n-1\) 阶矩阵 \(M_{ij}\) 称为 \(\bm A\) 的余子式, \(A_{ij}=(-1)^{i+j} M_{ij}\) 称为代数余子式.

定理 2.4.1: 行列式按第 \(i\) 行的展开式为 \(\displaystyle |\bm A|=\sum_{j=1}^n a_{ij}A_{ij}\), 按第 \(j\) 列的展开式为 \(\displaystyle |\bm A|=\sum_{i=1}^n a_{ij}A_{ij}\).

给定行指标的排列 \(i12\cdots(i-1)(i+1)\cdots n\), 展开得:

\[\begin{aligned} |\bm A| &=\sum_{jk_{1}\cdots k_{j-1}k_{j+1}\cdots k_{n}} (-1)^{r[i12\cdots (i-1)(i+1)\cdots n]+r(jk_{1}\cdots k_{j-1}k_{j+1}\cdots k_{n})} a_{ij}a_{1k_{1}}\cdots a_{i-1k_{i-1}}a_{i+1,k_{i+1}}\cdots a_{nk_{n}}\\&=\sum_{j=1}^{n}a_{ij}(-1)^{i-1}(-1)^{j-1}\Big[\sum_{k_{1}\cdots k_{j-1}k_{j+1}\cdots k_{n}}(-1)^{r(k_{1}\cdots k_{j-1}k_{j+1}\cdots k_{n})}a_{1k_{1}}\cdots a_{i-1,k_{i-1}}a_{i+1,k_{i+1}}\cdots a_{nk_{n}}\Big]\\&=\sum_{j=1}^{n}(-1)^{i+j}a_{ij}\begin{vmatrix}a_{11}&\cdots&a_{1,j-1}&a_{1,j+1}&\cdots&a_{1n}\\\vdots&&\vdots&\vdots&&\vdots\\a_{i+1,1}&\cdots&a_{i-1,j-1}&a_{i-1,j+1}&\cdots&a_{i-1,n}\\a_{i+1,1}&\cdots&a_{i+1,j-1}&a_{i+1,j+1}&\cdots&a_{i+1,n}\\\vdots&&\vdots&\vdots&&\vdots\\a_{n1}&\cdots&a_{n,j-1}&a_{n,j+1}&\cdots&a_{nn}\end{vmatrix}\\ &=\sum_{j=1}^n(-1)^{i+j}a_{ij}M_{ij}\:=\:\sum_{j=1}^na_{ij}A_{ij}\end{aligned} \]

定理 2.4.3: 行列式 \(|\bm A|\) 第 \(i\) 行元素和第 \(k\) 行相应的代数余子式的乘积之和为 0, 即 \(\displaystyle \sum_{j=1}^n a_{ij} A_{kj}=0,\:(i\neq k)\).

构造一行列式 \(|\bm B|\), 它与 \(|\bm A|\) 相同, 但第 \(k\) 行元素替换为 \(|\bm A|\) 的第 \(i\) 行元素, 对 \(|\bm B|\) 按第 \(k\) 行展开得

\[|\bm B|=\sum_{j=1}^n a_{ij} A_{kj}=0 \]

范德蒙德行列式:

\[\begin{vmatrix}1&1&1&\cdots&1\\ a_1&a_2&a_3&\cdots&a_n\\ a_1^2&a_2^2&a_3^2&\cdots&a_n^2\\ \vdots&\vdots&\vdots&&\vdots\\ a_1^{n-2}&a_2^{n-2}&a_3^{n-2}&\cdots&a_n^{n-2}\\ a_1^{n-1}&a_2^{n-1}&a_3^{n-1}&\cdots&a_n^{n-1} \end{vmatrix}=\prod_{1\leq i<j \leq n}(a_j-a_i) \]

证明: 当 \(n=2\) 时, 显然成立. 设对 \(n-1\) 成立, 则对 \(n\),

\[\begin{aligned} \begin{vmatrix}1&1&1&\cdots&1\\ a_1&a_2&a_3&\cdots&a_n\\ a_1^2&a_2^2&a_3^2&\cdots&a_n^2\\ \vdots&\vdots&\vdots&&\vdots\\ a_1^{n-2}&a_2^{n-2}&a_3^{n-2}&\cdots&a_n^{n-2}\\ a_1^{n-1}&a_2^{n-1}&a_3^{n-1}&\cdots&a_n^{n-1} \end{vmatrix}&=\begin{vmatrix}1&1&1&\cdots&1\\ 0&a_2-a_1&a_3-a_1&\cdots&a_n-a_1\\ 0&a_2^2-a_1a_2&a_3^2-a_1a_3&\cdots&a_n^2-a_1a_n\\ \vdots&\vdots&\vdots&&\vdots\\ 0&a_2^{n-2}-a_1a_2^{n-3}&a_3^{n-2}-a_1a_3^{n-3}&\cdots&a_n^{n-2}-a_1a_n^{n-3}\\ 0&a_2^{n-1}-a_1a_2^{n-2}&a_3^{n-1}-a_1a_3^{n-2}&\cdots&a_n^{n-1}-a_1a_n^{n-2} \end{vmatrix}\\&=(a_2-a_1)(a_3-a_1)\cdots(a_n-a_1) \begin{vmatrix}1&1&\cdots&1\\ a_2&a_3&\cdots&a_n\\ a_2^2&a_3^2&\cdots&a_n^2\\ \vdots&\vdots&&\vdots\\ a_2^{n-2}&a_3^{n-2}&\cdots&a_n^{n-2} \end{vmatrix}\\&=(a_2-a_1)(a_3-a_1)\cdots(a_n-a_1)\prod_{2\leq i<j \leq n}(a_j-a_i)\\ &=\prod_{1\leq i<j \leq n}(a_j-a_i) \end{aligned} \]

例 2.4.4:

\[D_n=\begin{vmatrix}x&0&0&\cdots&0&0&a_0\\ -1&x&0&\cdots&0&0&a_1\\ 0&-1&x&\cdots&0&0&a_2\\ \vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&-1&x&a_{n-2}\\ 0&0&0&\cdots&0&-1&x+a_{n-1} \end{vmatrix} \]

\(D_2=\begin{vmatrix}x & a_0\\ -1 & x+a_1 \end{vmatrix}=x^2+a_1 x-a_0\), 设 \(D_{n-1}=x^{n-1}+a_{n-2}x^{n-2}+\cdots+a_0\), 则按第一行展开:

\[\begin{aligned} D_n&=x \begin{vmatrix} x&0&\cdots&0&0&a_1\\ -1&x&\cdots&0&0&a_2\\ \vdots&\vdots&&\vdots&\vdots&\vdots\\ 0&0&\cdots&-1&x&a_{n-2}\\ 0&0&\cdots&0&-1&x+a_{n-1} \end{vmatrix}+(-1)^{n+1}a_0 \begin{vmatrix} -1&x&0&\cdots&0&0\\ 0&-1&x&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&\cdots&-1&x\\ 0&0&0&\cdots&0&-1 \end{vmatrix}\\&=x(x^{n-1}+a_{n-1}x^{n-2}+\cdots+a_1)+(-1)^{n+1}a_0(-1)^{n-1}\\ &=x^n+a_{n-1}x^{n-1}+\cdots+a_0\end{aligned} \]

例 2.4.5:

\[D_n=\begin{vmatrix}2&-1&0&0&\cdots&0&0&0\\ -1&2&-1&0&\cdots&0&0&0\\ 0&-1&2&-1&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 0&0&0&0&\cdots&-1&2&-1\\ 0&0&0&0&\cdots&0&-1&2\end{vmatrix} \]

把第 \(2,\cdots,n\) 列都加到第 1 列, 再按第一列展开,

\[\begin{aligned} D_n&=\begin{vmatrix}1&-1&0&0&\cdots&0&0&0\\ 0&2&-1&0&\cdots&0&0&0\\ 0&-1&2&-1&\cdots&0&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 0&0&0&0&\cdots&-1&2&-1\\ 1&0&0&0&\cdots&0&-1&2\end{vmatrix}\\&=D_{n-1}+(-1)^{n+1}(-1)^{n-1}=D_{n-1}+1\end{aligned} \]

故 \(D_n=D_1+n-1=n+1\).

例 2.4.6:

\[D_n=\begin{vmatrix}a+b&ab&0&0&\cdots&0&0\\ 1&a+b&ab&0&\cdots&0&0\\ 0&1&a+b&ab&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&0&\cdots&1&a+b\end{vmatrix} \]

按第一行展开:

\[\begin{aligned} D_n&=(a+b)\begin{vmatrix} a+b&ab&0&\cdots&0&0\\ 1&a+b&ab&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&\cdots&1&a+b\end{vmatrix} -ab \begin{vmatrix} 1&ab&0&\cdots&0&0\\ 0&a+b&ab&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&\cdots&1&a+b\end{vmatrix}\\ &=(a+b)D_{n-1} -abD_{n-2} \end{aligned} \]

故 \(D_n-aD_{n-1}=b(D_{n-1}-aD_{n-2})\). 于是 \(D_n-aD_{n-1}=b^{n-2}(D_2-aD_1)=b^n\),

同时 \(D_n-bD_{n-1}=a(D_{n-1}-bD_{n-2})\), 于是 \(D_n-bD_{n-1}=a^n\), 所以

\[D_n=\frac{a^{n+1}-b^{n+1}}{a-b} \]

例 2.4.7:

\[|A|=\begin{vmatrix} 1&2&3&\cdots&n-1&n\\ n&1&2&\cdots&n-2&n-1\\ n-1&n&1&\cdots&n-3&n-2\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 2&3&4&\cdots&n&1 \end{vmatrix} \]

用第二行减第一行, 第三行减第二行,..., 第 \(n\) 行减 \(n-1\) 行, 再将所有列加到第一列:

\[\begin{aligned} |A|&=\begin{vmatrix} 1-n&1&1&\cdots&1&1\\ 1&1-n&1&\cdots&1&1\\ 1&1&1-n&\cdots&1&1\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 2&3&4&\cdots&n&1 \end{vmatrix} =\begin{vmatrix} 0&1&1&\cdots&1&1\\ 0&1-n&1&\cdots&1&1\\ 0&1&1-n&\cdots&1&1\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ \frac{n(n+1)}{2}&3&4&\cdots&n&1 \end{vmatrix}\\&=(-1)^{n+1}\frac{n(n+1)}{2} \begin{vmatrix} 1&1&\cdots&1&1\\ 1-n&1&\cdots&1&1\\ 1&1-n&\cdots&1&1\\ \vdots&\vdots&&\vdots&\vdots\\ 1&1&\cdots&1-n&1 \end{vmatrix}\\&=(-1)^{n+1}\frac{n(n+1)}{2} \begin{vmatrix} 1&1&\cdots&1&1\\ -n&0&\cdots&0&0\\ 0&-n&\cdots&0&0\\ \vdots&\vdots&&\vdots&\vdots\\ 0&0&\cdots&-n&0 \end{vmatrix}\\&=(-1)^{n+1}\frac{n(n+1)}{2} (-1)^{r[(n-1)1\cdots (n-2)]}(-n)^{n-2}=(-1)^{n-1} n^{n-1}\frac{n+1}{2}\end{aligned} \]

例 2.4.8: 设数域 \(K\) 上的 \(n\) 阶矩阵 \(\bm A\) ,其元素的代数余子式为 \(A_{ij}\). 给 \(\bm A\) 的每个元素加 \(t\) 得到 \(\bm A(t)=(a_{ij}+t)\), 证明

\[|\bm A(t)|=|\bm A|+t\sum_{i=1}^n \sum_{j=1}^n A_{ij} \]

将 \(|\bm A(t)|\) 拆开得到 \(2^n\) 个行列式, 其中含有两列以上 \(t\) 的行列式都为 0, 故

\[\begin{aligned} |\bm A(t)|&=\begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n}\\ a_{21} & a_{22} &\cdots & a_{2n}\\ \vdots & \vdots & & \vdots\\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}+\begin{vmatrix} t & a_{12} & \cdots & a_{1n}\\ t & a_{22} &\cdots & a_{2n}\\ \vdots & \vdots & & \vdots\\ t & a_{n2} & \cdots & a_{nn} \end{vmatrix}+\cdots+ \begin{vmatrix} a_{11} & a_{12} & \cdots & t\\ a_{21} & a_{22} &\cdots & t\\ \vdots & \vdots & & \vdots\\ a_{n1} & a_{n2} & \cdots & t \end{vmatrix}\\&=|\bm A|+\sum_{i=1}^n tA_{i1}+\cdots+\sum_{i=1}^n tA_{in}\\ &=|\bm A|+t\sum_{i=1}^n \sum_{j=1}^n A_{ij}\end{aligned} \]

例 2.4.9:

\[D_n=\begin{vmatrix}1&1&1&\cdots&1&1\\ 1&C_2^1&C_3^1&\cdots&C_{n-1}^1&C_n^1\\ 1&C_3^2&C_4^2&\cdots&C_n^2&C_{n+1}^2\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 1&C_{n-1}^{n-2}&C_n^{n-2}&\cdots&C_{2n-4}^{n-2}&C_{2n-3}^{n-2}\\ 1&C_n^{n-1}&C_{n+1}^{n-1}&\cdots&C_{2n-3}^{n-1}&C_{2n-2}^{n-1} \end{vmatrix} \]

\(C_n^k-C_{n-1}^{k-1}=C_{n-1}^k\), 于是, 用第 \(n-1\) 行减第 \(n\) 行,...,用第一行减第二行:

\[\begin{aligned} D_n&=\begin{vmatrix} 1&1&1&\cdots&1&1\\ 0&C_1^1&C_2^1&\cdots&C_{n-2}^1&C_{n-1}^1\\ 0&C_2^2&C_3^2&\cdots&C_{n-1}^2&C_{n}^2\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&C_{n-2}^{n-2}&C_{n-1}^{n-2}&\cdots&C_{2n-5}^{n-2}&C_{2n-4}^{n-2}\\ 0&C_{n-1}^{n-1}&C_{n}^{n-1}&\cdots&C_{2n-4}^{n-1}&C_{2n-3}^{n-1} \end{vmatrix} =\begin{vmatrix} 1&C_2^1&\cdots&C_{n-2}^1&C_{n-1}^1\\ 1&C_3^2&\cdots&C_{n-1}^2&C_{n}^2\\ \vdots&\vdots&&\vdots&\vdots\\ 1&C_{n-1}^{n-2}&\cdots&C_{2n-5}^{n-2}&C_{2n-4}^{n-2}\\ 1&C_{n}^{n-1}&\cdots&C_{2n-4}^{n-1}&C_{2n-3}^{n-1} \end{vmatrix}\\&=\begin{vmatrix} 1&C_2^1&\cdots&C_{n-2}^1&C_{n-1}^1\\ 0&C_2^2&\cdots&C_{n-2}^2&C_{n-1}^2\\ \vdots&\vdots&&\vdots&\vdots\\ 0&C_{n-2}^{n-2}&\cdots&C_{2n-6}^{n-2}&C_{2n-5}^{n-2}\\ 0&C_{n-1}^{n-1}&\cdots&C_{2n-5}^{n-1}&C_{2n-4}^{n-1} \end{vmatrix} =\begin{vmatrix} 1&\cdots&C_{n-2}^2&C_{n-1}^2\\ \vdots&&\vdots&\vdots\\ 1&\cdots&C_{2n-6}^{n-2}&C_{2n-5}^{n-2}\\ 1&\cdots&C_{2n-5}^{n-1}&C_{2n-4}^{n-1}\\ \end{vmatrix}\\&=\cdots=\begin{vmatrix} 1 & C_{n-1}^{n-2}\\ 1 & C_{n}^{n-1} \end{vmatrix}=1\end{aligned} \]

例 2.4.10:

\[D_n=\begin{vmatrix}1&x_1+a_{11}&x_1^2+a_{21}x_1+a_{22}&\cdots&x_1^{n-1}+a_{n-1,1}x_1^{n-2}+\cdots+a_{n-1,n-1}\\1&x_2+a_{11}&x_2^2+a_{21}x_2+a_{22}&\cdots&x_2^{n-1}+a_{n-1,1}x_2^{n-2}+\cdots+a_{n-1,n-1}\\\vdots&\vdots&\vdots&&\vdots\\1&x_n+a_{11}&x_n^2+a_{21}x_n+a_{22}&\cdots&x_n^{n-1}+a_{n-1,1}x_n^{n-2}+\cdots+a_{n-1,n-1}\end{vmatrix} \]

可以拆成 \(n!\) 个行列式之和, 其中不为 0 的行列式只有 1 个:

\[D_n=\begin{array}{|ccccc|}1&x_1&x_1^2&\cdots&x_1^{n-1}\\[1ex]1&x_2&x_2^2&\cdots&x_2^{n-1}\\[1ex]\vdots&\vdots&\vdots&&\vdots\\[1ex]1&x_n&x_n^2&\cdots&x_n^{n-1}\end{array}=\prod_{1\leq i<j\leq n}(x_j-x_i) \]

例 2.4.11:

\[D_n=\begin{vmatrix}1&1&\cdots&1&1\\x_1&x_2&\cdots&x_{n-1}&x_n\\x_1^2&x_2^2&\cdots&x_{n-1}^2&x_n^2\\\vdots&\vdots&&\vdots&\vdots\\x_1^{n-2}&x_2^{n-2}&\cdots&x_{n-1}^{n-2}&x_n^{n-2}\\x_1^n&x_2^n&\cdots&x_{n-1}^n&x_n^n\end{vmatrix} \]

为了利用范德蒙行列式, 在第 \(n-1\) 行插入 \((x_1^{n-1},\cdots,x_n^{n-1})\), 并在右边添加第 \(n+1\) 列 \((1,y,\cdots, y^n)\):

\[\bar D_{n+1}=\begin{vmatrix}1&1&\cdots&1&1&1\\x_1&x_2&\cdots&x_{n-1}&x_n&y\\x_1^2&x_2^2&\cdots&x_{n-1}^2&x_n^2&y^2\\\vdots&\vdots&&\vdots&\vdots&\vdots\\x_1^{n-2}&x_2^{n-2}&\cdots&x_{n-1}^{n-2}&x_n^{n-2}&y^{n-2}\\x_1^{n-1}&x_2^{n-1}&\cdots&x_{n-1}^{n-1}&x_n^{n-1}&y^{n-1}\\x_1^n&x_2^n&\cdots&x_{n-1}^n&x_n^n&y^n\end{vmatrix}=(y-x_1)\cdots(y-x_n)\prod_{1\leq i<j\leq n}(x_j-x_i) \]

按第 \(n+1\) 列展开, 可以看出 \(y^{n-1}\) 项为 \((-1)^{2n+1}D_ny^{n-1}\), 故

\[(-1)^{2n+1}D_n=-\sum_{i=1}^n x_i \prod_{1\leq i<j\leq n}(x_j-x_i)\\ D_n=\sum_{i=1}^n x_i \prod_{1\leq i<j\leq n}(x_j-x_i) \]

习题 2.4.6:

\[\begin{vmatrix}1&2&2&\cdots&2&2&2\\ 2&2&2&\cdots&2&2&2\\ 2&2&3&\cdots&2&2&2\\ \vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 2&2&2&\cdots&2&n-1&2\\ 2&2&2&\cdots&2&2&n \end{vmatrix} \]

‍

用第一行减其他行, 再按第二行展开,

\[\begin{aligned} |\bm A|&=\begin{vmatrix} 1&2&2&\cdots&2&2&2\\ 1&0&0&\cdots&0&0&0\\ 1&0&1&\cdots&0&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 1&0&0&\cdots&0&n-3&0\\ 1&0&0&\cdots&0&0&n-2 \end{vmatrix}=\begin{vmatrix} 0&2&2&\cdots&2&2&2\\ 1&0&0&\cdots&0&0&0\\ 0&0&1&\cdots&0&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots&\vdots\\ 0&0&0&\cdots&0&n-3&0\\ 0&0&0&\cdots&0&0&n-2 \end{vmatrix}\\&=-\begin{vmatrix} 2&2&\cdots&2&2\\ 0&1&\cdots&0&0\\ \vdots&\vdots&&\vdots&\vdots\\ 0&0&\cdots&n-3&0\\ 0&0&\cdots&0&n-2 \end{vmatrix} =-2(n-2)!\end{aligned} \]

习题 2.4.7:

\[D_n=\begin{vmatrix}x&y&y&\cdots&y&y\\ z&x&y&\cdots&y&y\\ z&z&x&\cdots&y&y\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ z&z&z&\cdots&x&y\\ z&z&z&\cdots&z&x \end{vmatrix},\:y\neq z \]

用第二行减第一行, 再按第一行展开

\[\begin{aligned} D_n&=\begin{vmatrix} x-z&y-x&0&\cdots&0&0\\ z&x&y&\cdots&y&y\\ z&z&x&\cdots&y&y\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ z&z&z&\cdots&x&y\\ z&z&z&\cdots&z&x \end{vmatrix}\\&=(x-z)D_{n-1}+(x-y)\begin{vmatrix} z&y&y&\cdots&y&y\\ z&x&y&\cdots&y&y\\ z&z&x&\cdots&y&y\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ z&z&z&\cdots&x&y\\ z&z&z&\cdots&z&x \end{vmatrix}\\&=(x-z)D_{n-1}+(x-y)\begin{vmatrix} z&y&y&\cdots&y&y\\ 0&x-y&0&\cdots&0&0\\ 0&0&x-y&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&\cdots&x-y&0\\ 0&0&0&\cdots&0&x-y \end{vmatrix}\\&=(x-z)D_{n-1}+z(x-y)^{n-1}\end{aligned} \]

若用第二列减第一列, 对称地得到 \(D_n=(x-y)D_{n-1}+y(x-z)^{n-1}\). 于是

\[D_n=\frac{z(x-y)^n-y(x-z)^n}{z-y} \]

习题 2.4.9: 利用例 2.4.8 的结果, 计算:

\[(1)\begin{vmatrix}1+x_1y_1&1+x_1y_2&\cdots&1+x_1y_n\\ 1+x_2y_1&1+x_2y_2&\cdots&1+x_2y_n\\ \vdots&\vdots&&\vdots\\ 1+x_ny_1&1+x_ny_2&\cdots&1+x_ny_n \end{vmatrix} ,\quad (2)\begin{vmatrix} 1+t&t&t&...&t\\ t&2+t&t&...&t\\ t&t&3+t&...&t\\ \vdots&\vdots&\vdots&&\vdots\\ t&t&t&...&n+t \end{vmatrix} \]

(1)

\[(1)=\begin{vmatrix}x_1y_1&x_1y_2&\cdots&x_1y_n\\ x_2y_1&x_2y_2&\cdots&x_2y_n\\ \vdots&\vdots&&\vdots\\ x_ny_1&x_ny_2&\cdots&x_ny_n \end{vmatrix}+\sum_{i=1}^n\sum_{j=1}^n A_{ij}=|\bm A|+\sum_{i=1}^n\sum_{j=1}^n A_{ij} \]

其中 \(A_{ij}\) 为 \(|\bm A|\) 的代数余子式. 注意到 \(n\geq3\) 时, \(|\bm A|\) 和 \(A_{ij}\) 中各行都成比例, 故 \((1)=0\).

(2)

\[(2)=diag(1,2,\cdots,n)+t\sum_{i=1}^n\sum_{j=1}^n A_{ij} \]

其中 \(A_{ij}\) 是 \(diag(1,\cdots,n)\) 的代数余子式. 注意到 \(i=j\) 时 \(A_{ij}=n!/i\), 其余情况 \(A_{ij}=0\), 故

\[(2)=n!+tn!\Big(1+\frac12+\cdots\frac1n\Big)=n!\Big(1+t+\frac t2+\cdots\frac tn\Big) \]

习题 2.4.14:

\[D_n=\begin{vmatrix} 1-a_1&a_2&0&0&\cdots&0&0\\ -1&1-a_2&a_3&0&\cdots&0&0\\ 0&-1&1-a_3&a_4&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&0&\cdots &1-a_{n-1}&a_n \\ 0&0&0&0&\cdots&-1&1-a_n \end{vmatrix} \]

按第 \(n\) 行展开, 得到

\[\begin{aligned} D_n&=(1-a_n)D_{n-1}-(-1)^{2n-1} \begin{vmatrix} 1-a_1&a_2&0&0&\cdots&0&0\\ -1&1-a_2&a_3&0&\cdots&0&0\\ 0&-1&1-a_3&a_4&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\ 0&0&0&0&\cdots &a_{n-1}&0 \\ 0&0&0&0&\cdots&-1&a_n \end{vmatrix}\\&=(1-a_n)D_{n-1}+a_nD_{n-2} \end{aligned} \]

于是

\[\begin{aligned} D_n-D_{n-1}&=-a_n(D_{n-1}-D_{n-2})\\ &=(-1)^{n-2}a_n\cdots a_3(D_2-D_1)\\ &=(-1)^na_n\cdots a_1 \end{aligned} \]

所以

\[D_n=(-1)^n a_n\cdots a_1+(-1)^{n-1}a_{n-1}\cdots a_1+\cdots-a_1+1 \]

行列式计算总结

Cramer 法则

定理 2.5.1: 数域 \(K\) 上 \(n\) 个方程的 \(n\) 元线性方程组有唯一解的充要条件是系数行列式 \(|\bm A|\neq0\).

定理 2.5.2: \(n\) 个方程的 \(n\) 元线性方程组的唯一解是

\[\bm x=\left(\frac{|\bm B_1|}{|\bm A|},\cdots,\frac{|\bm B_n|}{|\bm A|} \right)^T \]

其中

\[\bm B_j=\begin{pmatrix}a_{11}&\cdots&a_{1,j-1}&b_1&a_{1,j+1}&\cdots&a_{1n}\\a_{21}&\cdots&a_{2,j-1}&b_2&a_{2,j+1}&\cdots&a_{2n}\\\vdots&&\vdots&\vdots&\vdots&&\vdots\\a_{n1}&\cdots&a_{n,j-1}&b_n&a_{n,j+1}&\cdots&a_{nn}\end{pmatrix} \]

把 \(\bm x\) 代入第 \(i\) 个方程 \(a_{i1}x_1+\cdots a_{in}x_n=b_i\) 的左边, 得

\[\begin{aligned} a_{i1}\frac{|\bm B_1|}{|\bm A|}+\cdots+a_{in}\frac{|\bm B_n|}{|\bm A|}&=\frac{1}{|\bm A|}\sum_{j=1}^n a_{ij}|\bm B_j|\\ &=\frac{1}{|\bm A|} \sum_{j=1}^n a_{ij} \sum_{k=1}^n b_k A_{kj}\\ &=\frac{1}{|\bm A|} \sum_{k=1}^n b_k \sum_{j=1}^n a_{ij}A_{kj}\\ &=\frac{1}{|\bm A|} b_i \sum_{j=1}^n a_{ij}A_{ij} \quad(只有k=i项不为 0)\\ &=b_i \end{aligned} \]

由此看出, 利用行列式的性质 2, 性质 4, 性质 7 和按列展开定理, 就可解决线性方程组解的问题.

拉普拉斯定理 (按 k 行展开)

定义 2.6.1: 在 \(n\) 阶矩阵 \(\bm A\) 中任取 \(k\) 行 \(k\) 列, 位于这些行和列交叉处的元素按原来顺序组成的 \(k\) 阶行列式称为 \(\bm A\) 的 \(k\) 阶子式, 记作

\[\bm A\begin{pmatrix}i_1,i_2,\cdots,i_k \\ j_1,j_2,\cdots,j_k \end{pmatrix} \]

余下元素按原来顺序组成的 \(n-k\) 阶行列式称为余子式, 乘以 \((-1)^{(i_1+\cdots+i_k)+(j_1+\cdots j_k)}\) 得到代数余子式,

\[(-1)^{(i_1+\cdots+i_k)+(j_1+\cdots j_k)} \bm A\begin{pmatrix}i_1',i_2',\cdots,i_{n-k}' \\ j_1',j_2',\cdots,j_{n-k}' \end{pmatrix} \]

定理 2.6.1 (Laplace) : 在 \(n\) 阶矩阵 \(\bm A\) 中取第 \(i_1,\cdots i_k\:(i_1<\cdots<i_k)\) 行, 则

\[|\bm A|=\sum_{1\leq j_1<\cdots<j_k\leq n} \bm A\begin{pmatrix}i_1,i_2,\cdots,i_k \\ j_1,j_2,\cdots,j_k \end{pmatrix}\cdot (-1)^{(i_1+\cdots+i_k)+(j_1+\cdots j_k)} \bm A\begin{pmatrix}i_1',i_2',\cdots,i_{n-k}' \\ j_1',j_2',\cdots,j_{n-k}' \end{pmatrix} \]

给定行指标的一个排列 \(i_1\cdots i_ki_1'\cdots i_{n-k}'\), 有

\[|\bm A|=\sum_{\mu_1\cdots\mu_k\nu_1\cdots\nu_{n-k}} (-1)^{r(i_1\cdots i_ki_1'\cdots i_{n-k}')+r(\mu_1\cdots\mu_k\nu_1\cdots\nu_{n-k})} a_{i_1\mu_1}\cdots a_{i_k\mu_k}a_{i_1'\nu_1}\cdots a_{i_{n-k}'\nu_{n-k}} \]

共有 \(n!\) 项. 对给定的第 \(i_1,\cdots i_k\) 行, 任意取定 \(k\) 列 \(1\leq j_1<\cdots<j_k\leq n\), 把 \(n!\) 项分成 \(C_n^k\) 组:

每组内 \(\mu_1\cdots\mu_k\) 是 \(j_1\cdots j_k\) 的排列, \(\nu_1\cdots\nu_{n-k}\) 是 \(j_1'\cdots j_{n-k}'\) 的排列, 由例 2.1.5得

\[(-1)^{r(\mu_1\cdots\mu_k\nu_1\cdots\nu_{n-k})}=(-1)^{r(\mu_1\cdots\mu_k)+r(\nu_1\cdots\nu_{n-k})+(j_1+\cdots +j_k)+\frac12 k(k+1)} \]

于是

\[\begin{aligned} |\bm A|&=\sum_{\mu_1\cdots\mu_k\nu_1\cdots\nu_{n-k}} (-1)^{r(i_1\cdots i_ki_1'\cdots i_{n-k}')+r(\mu_1\cdots\mu_k\nu_1\cdots\nu_{n-k})} a_{i_1\mu_1}\cdots a_{i_k\mu_k}a_{i_1'\nu_1}\cdots a_{i_{n-k}'\nu_{n-k}}\\&=\sum_{1\leq j_1<\cdots<j_k\leq n} \sum_{\mu_1\cdots\mu_k}\sum_{\nu_1\cdots\nu_{n-k}} (-1)^{r(i_1\cdots i_k)+r(i_1'\cdots i_{n-k}')+(i_1+\cdots+i_k)+\frac12 k(k+1)}\\&\qquad \cdot (-1)^{r(\mu_1\cdots\mu_k)+r(\nu_1\cdots\nu_{n-k})+(j_1+\cdots +j_k)+\frac12 k(k+1)}a_{i_1\mu_1}\cdots a_{i_k\mu_k}a_{i_1'\nu_1}\cdots a_{i_{n-k}'\nu_{n-k}}\\&=\sum_{1\leq j_1<\cdots<j_k\leq n}(-1)^{(i_1+\cdots+i_k)+(j_1+\cdots j_k)} \\ &\qquad\cdot\sum_{\mu_1\cdots\mu_k}(-1)^{r(\mu_1\cdots\mu_k)} a_{i_1\mu_1}\cdots a_{i_k\mu_k} \sum_{\nu_1\cdots\nu_{n-k}}(-1)^{r(\nu_1\cdots\nu_{n-k})}a_{i_1'\nu_1}\cdots a_{i_{n-k}'\nu_{n-k}}\\&=\sum_{1\leq j_1<\cdots<j_k\leq n}(-1)^{(i_1+\cdots+i_k)+(j_1+\cdots j_k)} \bm A\begin{pmatrix}i_1,i_2,\cdots,i_k \\ j_1,j_2,\cdots,j_k \end{pmatrix} \bm A\begin{pmatrix}i_1',i_2',\cdots,i_{n-k}' \\ j_1',j_2',\cdots,j_{n-k}' \end{pmatrix} \end{aligned} \]

推论 2.6.1:

\[\begin{vmatrix}a_{11}&\cdots&a_{1k}&0&\cdots&0\\ \vdots&&\vdots&\vdots&&\vdots\\ a_{k1}&\cdots&a_{kk}&0&\cdots&0\\c_{11}&\cdots&c_{1k}&b_{11}&\cdots&b_{1r}\\ \vdots&&\vdots&\vdots&&\vdots\\c_{r1}&\cdots&c_{rk}&b_{r1}&\cdots&b_{rr}\end{vmatrix} =\begin{vmatrix}a_{11}&\cdots&a_{1k}\\ \vdots&&\vdots\\a_{k1}&\cdots&a_{kk}\end{vmatrix} \cdot\begin{vmatrix}b_{11}&\cdots&b_{1r}\\ \vdots&&\vdots\\b_{r1}&\cdots&b_{rr}\end{vmatrix} \]

按前 \(k\) 行展开, 所形成的 \(k\) 阶子式只有 \(\bm A\begin{pmatrix}1,2,\cdots,k\\ 1,2,\cdots,k \end{pmatrix}=\begin{vmatrix}a_{11}&\cdots&a_{1k}\\ \vdots&&\vdots\\a_{k1}&\cdots&a_{kk}\end{vmatrix}\) 不含零列,

而它的余子式为 \(\begin{vmatrix}b_{11}&\cdots&b_{1r}\\ \vdots&&\vdots\\b_{r1}&\cdots&b_{rr}\end{vmatrix}\), 且 \((-1)^{(1+\cdots+k)+(1+\cdots+k)}=1\).

例 2.6.1:

\[\begin{aligned} \begin{vmatrix}0&\cdots&0&a_{11}&\cdots&a_{1k}\\ \vdots&&\vdots&\vdots&&\vdots\\0&\cdots&0&a_{k1}&\cdots&a_{kk}\\b_{11}&\cdots&b_{1r}&c_{11}&\cdots&c_{1k}\\ \vdots&&\vdots&\vdots&&\vdots\\b_{r1}&\cdots&b_{rr}&c_{r1}&\cdots&c_{rk}\end{vmatrix}&= \begin{vmatrix}a_{11}&\cdots&a_{1k}\\\vdots&&\vdots\\a_{k1}&\cdots&a_{kk}\end{vmatrix}(-1)^{(1+\cdots+k)+[(r+1)+\cdots+(r+k)]}\begin{vmatrix}b_{11}&\cdots&b_{1r}\\\vdots&&\vdots\\b_{r1}&\cdots&b_{rr}\end{vmatrix}\\&=(-1)^{kr}|\bm A||\bm B|\end{aligned} \]

例 2.6.3:

\[D_{2n}=\begin{vmatrix}a&&&&&b\\&\ddots&&&⋰&\\&&a&b&&\\&&b&a&&\\&⋰&&&\ddots&\\b&&&&&a\end{vmatrix} \]

按第一行和第 \(n\) 行展开, 只有第 1,n 列的余子式不含零列,

\[D_{2n}=(a^2-b^2)(-1)^{2(1+2n)}D_{2n-2}=\cdots=(a^2-b^2)^n \]

行列式应用举例

例 2.7.2: 若 \(F(t) = \begin{vmatrix}f_{11}(t)&f_{12}(t)&\cdots&f_{1n}(t)\\f_{21}(t)&f_{22}(t)&\cdots&f_{2n}(t)\\\vdots&\vdots&&\vdots\\f_{n1}(t)&f_{n2}(t)&\cdots&f_{nn}(t)\end{vmatrix}\), 证明

\[\frac{\mathrm{d}}{\mathrm{d}t}F(t) = \sum_{j=1}^{n}\begin{vmatrix}f_{11}(t)&f_{12}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{1j}(t)&\cdots&f_{1n}(t)\\[2pt] f_{21}(t)&f_{22}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{2j}(t)&\cdots&f_{2n}(t)\\\vdots&\vdots&&\vdots&&\vdots\\ f_{n1}(t)&f_{n2}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{nj}(t)&\cdots&f_{nn}(t)\end{vmatrix} \]

\[\begin{aligned} F'(t)&=\frac{\mathrm d}{\mathrm dt} \sum_{i_1\cdots i_n}(-1)^{r(i_1\cdots i_n)} f_{i_11}\cdots f_{i_nn}\\ &=\sum_{i_1\cdots i_n} (-1)^{r(i_1\cdots i_n)} \sum_{j=1}^n f_{i_11}\cdots\frac{\mathrm d f_{i_jj}}{\mathrm dt} \cdots f_{i_nn}\\ &=\sum_{j=1}^n \sum_{i_1\cdots i_n} (-1)^{r(i_1\cdots i_n)} f_{i_11}\cdots\frac{\mathrm d f_{i_jj}}{\mathrm dt} \cdots f_{i_nn}\\ &=\sum_{j=1}^{n}\begin{vmatrix}f_{11}(t)&f_{12}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{1j}(t)&\cdots&f_{1n}(t)\\[2pt] f_{21}(t)&f_{22}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{2j}(t)&\cdots&f_{2n}(t)\\\vdots&\vdots&&\vdots&&\vdots\\ f_{n1}(t)&f_{n2}(t)&\cdots&\frac{\mathrm{d}}{\mathrm{d}t}f_{nj}(t)&\cdots&f_{nn}(t)\end{vmatrix} \end{aligned} \]

或者按列展开, 并使用归纳法.

例 2.7.8: 在数域 \(K\) 上, 设 \(a_1,\cdots, a_n\) 互不相同, 任意给定 \(b_1,\cdots,b_n\), 证明: 存在唯一的多项式 \(f(x)=c_1+c_2x+\cdots+c_nx^{n-1}\), 使得 \(f(a_i)=b_i,\:i=1,\cdots,n\).

把 \(c_1,\cdots,c_n\) 看作未知量, 则

\[\begin{bmatrix} 1 & a_1 &\cdots &a_1^{n-1}\\ 1 & a_2 &\cdots &a_2^{n-1}\\ \vdots&\vdots&&\vdots\\ 1 & a_n &\cdots &a_n^{n-1} \end{bmatrix} \begin{bmatrix} c_1\\ c_2 \\ \vdots \\ c_n \end{bmatrix}= \begin{bmatrix} b_1\\ b_2 \\ \vdots \\ b_n \end{bmatrix} \]

其系数行列式为范德蒙行列式: \(|\bm A|=\prod_{1\leq i<j\leq n}(a_j-a_i)\neq0\), 故 \(\bm c\) 有唯一解.

n 维向量空间

n 维向量空间 \(K^n\) 及其子空间

\[K^n=\{(a_1,\cdots,a_n):a_i\in K\} \]

规定加法: \((a_1,\cdots, a_n)+(b_1,\cdots,b_n)=(a_1+b_1,\cdots,a_n+b_n)\);

规定数乘: \(k(a_1,\cdots,a_n)=(ka_1,\cdots,ka_n)\).

容易验证加法和数乘满足如下 8 条运算法则: \(\forall \bm a,\bm b,\bm c\in K^n\), \(\forall k,l\in K\),

(1) \(\bm a+\bm b=\bm b+\bm a\);

(2) \((\bm a+\bm b)+\bm c=\bm a+(\bm b+\bm c)\);

(3) 定义 \(\bm0=(0,\cdots,0)\), 则 \(\bm a+\bm0=\bm a\);

(4) 定义 \(-\bm a=(-a_1,\cdots, -a_n)\), 则 \(\bm a+(-\bm a)=\bm0\);

(5) \(1\bm a=\bm a\);

(6) \((kl)\bm a=k(l\bm a)\);

(7) \((k+l)\bm a=k\bm a+l\bm a\);

(8) \(k(\bm a+\bm b)=k\bm a+k\bm b\);

定义 3.1.1: 数域 \(K\) 上所有 \(n\) 元有序数组组成的集合 \(K^n\), 连同定义在其上的加法和数乘运算, 及其满足的 8 条运算法则, 称为数域 \(K\)上的一个 \(n\) 维向量空间.

在 \(K^n\) 中, 给定 \(\bm\alpha_1,\cdots,\bm\alpha_n\), 若对于 \(\bm\beta\in K^n\), 存在 \(c_1,\cdots,c_n\in K\), 使得 \(\bm\beta=c_1\bm\alpha_1+\cdots+c_n\bm\alpha_n\), 则称 \(\bm\beta\) 可以由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

数域 \(K\) 上的方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm\beta\) 有解 \(\Longleftrightarrow\) \(\bm\beta\) 可以由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

将 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的所有线性组合组成一个集合: \(W=\{k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n:k_i\in K\}\), 易得 \(W\) 对加法和数乘封闭.

定义 3.1.2: \(K^n\) 的一个非空子集 \(U\) 满足:

(1) 若 \(\bm a,\bm b\in U\), 则 \(\bm a+\bm b\in U\);

(2) 若 \(\bm a\in U\), 则 \(\forall k\in K\), \(k\bm a\in U\).

则称 \(U\) 为 \(K^n\) 的线性子空间.

可见 \(W\) 是 \(K^n\) 的一个子空间, 称它为 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 张成的子空间, 记住 \(\langle\bm\alpha_1,\cdots,\bm\alpha_n\rangle\).

命题 3.1.1: 数域 \(K\) 上的方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm\beta\) 有解

      $\Longleftrightarrow$ $\bm\beta$ 可以由 $\bm\alpha_1,\cdots,\bm\alpha_n$ 线性表出$\Longleftrightarrow$ $\bm\beta\in\langle\bm\alpha_1,\cdots,\bm\alpha_n\rangle$

线性相关和线性无关的向量组

定义 3.2.1: 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\in K^n\), 若存在不全为 0 的数 \(k_1,\cdots,k_n\in K\), 使得

\[k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0 \]

则称 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关. 若

\[k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0 \Longrightarrow k_1,\cdots,k_n=0 \]

则称 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关.

(1) 包含 \(\bm0\) 的向量组必然线性相关;

(2) 单个向量 \(\bm\alpha\) 线性无关当且仅当 \(\alpha\neq0\).

考察线性相关和线性无关的不同角度:

(1) 向量组 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关 \(\Longleftrightarrow\) 其中至少一个向量可以用其余向量线性表出.

(2) \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关 \(\Longleftrightarrow\) 齐次方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0\) 有非零解; \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关 \(\Longleftrightarrow\) 齐次方程组只有零解.

(3) \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关 \(\Longleftrightarrow\) 行列式为 0; \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关 \(\Longleftrightarrow\) 行列式不为 0.

(4) 设 \(\bm\beta\) 可以被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 则 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关 \(\Longleftrightarrow\) 表出方式唯一.

(5) 若向量组的一个部分线性相关, 则向量组线性相关; 若向量组线性无关, 则向量组的任何一部分都线性无关.

(6) 若向量组线性无关, 则添上 \(m\) 个分量的延伸组也线性无关; 若向量组线性相关, 则缩短组也线性相关.

证明: 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的延伸组是 \(\tilde{\bm\alpha}_1,\cdots,\tilde{\bm\alpha}_n\), 因 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 故

\(k_1\tilde{\bm\alpha}_1+\cdots+k_n\tilde{\bm\alpha}_n=\bm0 \Longrightarrow k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0 \Longrightarrow k_1,\cdots,k_n=0\).

设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的缩短组是 \(\bar{\bm\alpha}_1,\cdots,\bar{\bm\alpha}_n\), 因 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关, 故

\(\exists k_1,\cdots,k_n\) 不全为零, 使得 \(k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0 \Longrightarrow k_1\bar{\bm\alpha}_1+\cdots+k_n\bar{\bm\alpha}_n=\bm0\).

命题 3.2.1: 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 则 \(\bm\beta\) 可以用 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出的充要条件是 \(\bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\) 线性相关.

\((\Rightarrow)\) 显然.

\((\Leftarrow)\) 若 \(\bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\) 线性相关, 则存在不全为 0 的 \(k_1,\cdots,k_n,l\), 使得

\[k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n+l\bm\beta=\bm0 \]

假如 \(l=0\) 则存在不全为 0 的 \(k_1,\cdots,k_n\) 使得 \(k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0\), 这与 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关矛盾.

故 \(l\neq0\), \(\bm\beta=-\frac{l}{k_1}\bm\alpha_1-\cdots-\frac{l}{k_n}\bm\alpha_n\).

例 3.2.2: 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 且

\[\begin{aligned} &\bm\beta_1=a_{11}\bm\alpha_1+\cdots+a_{1n}\bm\alpha_n\\ &\quad\vdots\\ &\bm\beta_n=a_{n1}\bm\alpha_1+\cdots+a_{nn}\bm\alpha_n \end{aligned} \]

证明 \(\bm\beta_1,\cdots,\bm\beta_n\) 线性无关的充要条件是

\[\begin{vmatrix}a_{11}&\cdots&a_{n1}\\ \vdots&&\vdots\\ a_{1n}&\cdots&a_{nn}\end{vmatrix}\neq0 \]

设 \(k_1\bm\beta_1+\cdots+k_n\bm\beta_n=\bm0\), 则 \((k_1a_{11}+\cdots+k_na_{n1})\bm\alpha_1+\cdots+(k_1a_{1n}+\cdots+k_na_{nn})\bm\alpha_n=\bm0\), 由于 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 故

\[\left\{\begin{aligned} &k_1a_{11}+\cdots+k_na_{n1}=0\\ &\quad \vdots\\ &k_1a_{1n}+\cdots+k_na_{nn}=0 \end{aligned}\right. \]

\(\bm\beta_1,\cdots,\bm\beta_n\) 线性无关 \(\Longleftrightarrow\) \(k_1,\cdots,k_n=0\) \(\Longleftrightarrow\) 齐次方程组只有零解 \(\Longleftrightarrow\) \(|\bm A|\neq0\).

例 3.2.3: 下面向量组是否线性相关

\[\bm{\alpha}_1=\begin{pmatrix}-1\\3\\2\\0\end{pmatrix}, \bm{\alpha}_2=\begin{pmatrix}4\\1\\2\\-3\end{pmatrix}, \bm{\alpha}_3=\begin{pmatrix}6\\2\\4\\-2\end{pmatrix}, \bm{\alpha}_4=\begin{pmatrix}3\\-2\\0\\1\end{pmatrix} \]

考虑齐次方程组 \(x_1\bm\alpha_1+\cdots+x_4\bm\alpha_4=\bm0\),

\[\begin{aligned}&\begin{pmatrix}-1&4&6&3\\3&1&2&-2\\2&2&4&0\\0&-3&-2&1\end{pmatrix}\longrightarrow\begin{pmatrix}-1&4&6&3\\0&13&20&7\\0&10&16&6\\0&-3&-2&1\end{pmatrix}\longrightarrow\begin{pmatrix}-1&4&6&3\\0&1&12&11\\0&5&8&3\\0&-3&-2&1\end{pmatrix}\\&\longrightarrow\begin{pmatrix}1&-4&-6&-3\\0&1&12&11\\0&0&-52&-52\\0&0&34&34\end{pmatrix}\longrightarrow\begin{pmatrix}1&-4&-6&-3\\0&1&12&11\\0&0&1&1\\0&0&0&0\end{pmatrix}\longrightarrow\begin{pmatrix}1&0&0&-1\\0&1&0&-1\\0&0&1&1\\0&0&0&0\end{pmatrix}\end{aligned} \]

故齐次方程组有非零解, 向量组线性相关, 令 \(x_4=1\), 得到 \(\bm\alpha_1+\bm\alpha_2-\bm\alpha_3+\bm\alpha_4=\bm0\).

例 3.2.4: 证明: \(K^n\) 中任意 \(n+1\) 个向量都线性相关.

考虑 \(x_1\bm\alpha_1+\cdots+x_{n+1}\bm\alpha_{n+1}=\bm0\), 它的未知数个数超过方程数, 因而有非零解, 所以 \(\bm\alpha_1,\cdots,\bm\alpha_{n+1}\) 线性相关.

例 3.2.6: 设 \(\bm\beta\) 可以被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 证明: \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关 \(\Longleftrightarrow\) 表出方式唯一.

\((\Rightarrow)\) 若 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 设有两种表出方式:

\[\bm\beta=k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n\\ \bm\beta=l_1\bm\alpha_1+\cdots+l_n\bm\alpha_n \]

相减得到 \((k_1-l_1)\bm\alpha_1+\cdots+(k_n-l_n)\bm\alpha_n=\bm0\), 因为线性无关, 故 \(k_1=l_1,\cdots,k_n=l_n\), 即表出方式唯一.

\((\Leftarrow)\) 若表出方式唯一, 即 \(\bm\beta=k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n\),

假设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关, 则存在不全为零的 \(l_1,\cdots,l_n\), 使得 \(l_1\bm\alpha_1+\cdots+l_n\bm\alpha_n=\bm0\),

两者相加, 得到 \(\bm\beta=(k_1+l_1)\bm\alpha_1+\cdots+(k_n+l_n)\bm\alpha_n\), 与表出方式唯一相矛盾.

例 3.2.7 (替换定理) : 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, \(\bm\beta=b_1\bm\alpha_1+\cdots+b_n\bm\alpha_n\). 如果 \(b_i\neq0\), 那么用 \(\bm\beta\) 替换 \(\bm\alpha_i\) 后得到的向量组\(\bm\alpha_1,\cdots,\bm\alpha_{i-1},\bm\beta,\bm\alpha_{i+1},\cdots,\bm\alpha_n\) 也线性无关.

利用例 3.2.2,

\[\left|\begin{array}{ccccccc}1&\cdots&0&b_1&0&\cdots&0\\0&\cdots&0&b_2&0&\cdots&0\\\vdots&&\vdots&\vdots&\vdots&&\vdots\\0&\cdots&1&b_{i-1}&0&\cdots&0\\0&\cdots&0&b_i&0&\cdots&0\\0&\cdots&0&b_{i+1}&1&\cdots&0\\\vdots&&\vdots&\vdots&\vdots&&\vdots\\0&\cdots&0&b_s&0&\cdots&1\end{array}\right|=b_i\neq0 \]

例 3.2.8: \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关的充要条件是: 每个 \(\bm\alpha_i\) 都不能用它前面的向量线性表出.

\((\Rightarrow)\) 若 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 假设某个 \(\bm\alpha_i\) 可被线性表出,

则 \(\bm\alpha_i=k_1\bm\alpha_1+\cdots+k_{i-1}\bm\alpha_{i-1}+0\bm\alpha_{i+1}+\cdots+0\bm\alpha_n\), 这与线性无关矛盾.

\((\Leftarrow)\) 若每个 \(\bm\alpha_i\) 都不能用它前面的向量线性表出, 假设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关, 则某个 \(\bm\alpha_i\) 可用其它向量线性表出,

\[\bm\alpha_i=k_1\bm\alpha_1+\cdots+k_{i-1}\bm\alpha_{i-1}+k_{i+1}\bm\alpha_{i+1}+\cdots+k_n\bm\alpha_n \]

若 \(k_n\neq0\), 则 \(\bm\alpha_n\) 可用前面向量线性表出. 若 \(k_n=0,k_{n-1}\neq0\), 则 \(\bm\alpha_{n-1}\) 可用前面向量线性表出,

以此类推, 若 \(k_n=0,\cdots,k_{i+1}=0\), 则 \(\bm\alpha_i\) 可用前面向量线性表出, 无论如何都引致矛盾.

例 3.2.11: 设 \(\bm H_{m\times n}\) 的列向量组为 \(\bm\alpha_1,\cdots,\bm\alpha_n\), 证明: \(\bm H\) 的任意 \(s\) 列都线性无关, 当且仅当齐次方程组

\[x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0 \]

的任一非零解的非零分量数大于 \(s\).

\((\Rightarrow)\) 若 \(\bm H\) 的任意 \(s\) 列都线性无关, 假设解 \(\bm x\) 含 \(t\leq s\) 个非零分量 \(x_{i_1},\cdots,x_{i_t}\), 则

\[x_{i_1}\bm\alpha_{i_1}+\cdots+x_{i_t}\bm\alpha_{i_t}=\bm0 \]

于是 \(x_{i_1}\bm\alpha_{i_1}+\cdots+x_{i_t}\bm\alpha_{i_t}+\cdots+x_{i_s}\bm\alpha_{i_s}=\bm0\) 有非零解, 与 \(\bm H\) 的任意 \(s\) 列都线性无关矛盾.

\((\Leftarrow)\) 若 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0\) 的任一非零解的非零分量数大于 \(s\), 假设 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_s}\) 线性相关, 则

\[x_{i_1}\bm\alpha_{i_1}+\cdots+x_{i_s}\bm\alpha_{i_s}=\bm0 \]

有非零解, 于是 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0\) 存在一个非零分量数小于等于 \(s\) 的解, 矛盾.

极大线性无关组, 向量组的秩

定义 3.3.1: 从向量组中取一个部分向量组, 使得此部分组线性无关, 且再加入任一其余向量都会使得此部分组线性相关, 则称这个部分组为极大线性无关组.

定义 3.3.2: 若向量组 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 的任一向量都可用 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性表出, 则称 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 可用 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性表出, 若两个向量组可以互相线性表出, 则称两个向量组等价, 记作 \(\{\bm\alpha_1,\cdots,\bm\alpha_s\}\cong \{\bm\beta_1,\cdots,\bm\beta_r \}\).

易证等价关系具有自反性, 对称性, 传递性.

命题 3.3.1: 向量组与它的极大线性无关组定价.

极大线性无关组作为部分向量组, 显然可以用原向量组线性表出.

设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的极大线性无关组为 \(\bm\alpha_1,\cdots,\bm\alpha_m\), 则对 \(i\geq m\), \(\bm\alpha_1,\cdots,\bm\alpha_m,\bm\alpha_i\) 线性相关,

由命题 3.2.1得, \(\bm\alpha_i\) 可用 \(\bm\alpha_1,\cdots,\bm\alpha_m\) 线性表出. 故 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 可用 \(\bm\alpha_1,\cdots,\bm\alpha_m\) 线性表出.

推论 3.3.1: 向量组的任意两个极大无关组等价.

由等价关系的传递性可得.

推论 3.3.2: \(\bm\beta\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出当且仅当 \(\bm\beta\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的极大无关组线性表出.

引理 3.3.1: 设 \(\bm\beta_1,\cdots,\bm\beta_r\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 线性表出, 若 \(r>s\), 则 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性相关.

因 \(\bm\beta_1,\cdots,\bm\beta_r\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 线性表出, 可设

\[\begin{aligned} &\bm\beta_1=a_{11}\bm\alpha_1+\cdots+a_{1s}\bm\alpha_s\\ &\quad\vdots\\ &\bm\beta_r=a_{r1}\bm\alpha_1+\cdots+a_{rs}\bm\alpha_s \end{aligned} \]

设 \(x_1\bm\beta_1+\cdots+x_r\bm\beta_r=(x_1a_{11}+\cdots+x_ra_{r1})\bm\alpha_1+\cdots+(x_1a_{1s}+\cdots+x_ra_{rs})\bm\alpha_s=\bm0\), 这相当于

\[\begin{cases}a_{11}x_1+a_{12}x_2+\cdots+a_{r1}x_r=0\\ \quad\vdots\\ a_{1s}x_1+a_{s2}x_2+\cdots+a_{rs}x_r=0\end{cases} \]

当 \(r>s\) 时, 未知量数大于方程数, 存在非零解, 故 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性相关.

推论 3.3.3: 设 \(\bm\beta_1,\cdots,\bm\beta_r\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 线性表出, 若 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性无关, 则 \(r\leq s\).

推论 3.3.4: 等价的线性无关向量组所含的向量数相同.

由推论 3.3.3 即可得.

推论 3.3.5: 向量组的任意两个极大无关组所含向量数相等.

由推论 3.3.1和推论 3.3.4 可得.

定义 3.3.2: 向量组的极大无关组所含向量数称为向量组的秩.

命题 3.3.2: 向量组线性无关的充要条件是它的秩等于向量数.

\(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关 \(\Longleftrightarrow\) 极大无关组是向量组自身 \(\Longleftrightarrow\) \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=n\).

命题 3.3.3: 若向量组 \((I)\) 可被向量组 \((II)\) 线性表出, 则 \(\mathrm{rank}(I)\leq \mathrm{rank}(II)\).

若向量组 \((I)\) 可被向量组 \((II)\) 线性表出, 则向量组 \((I)\) 的极大无关组可被向量组 \((II)\) 的极大无关组线性表出, 由推论 3.3.3 得 \(\mathrm{rank}(I)\leq \mathrm{rank}(II)\).

命题 3.3.4: 等价的向量组有相同的秩. (秩相等的向量组不一定等价)

例 3.3.2: 设 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=r\), 证明 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 中任意 \(r\) 个线性无关的向量都构成极大无关组.

设 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 是一个极大无关组, 设 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 线性无关.

任取余下的向量 \(\bm\alpha_l\), 因为 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r},\bm\alpha_l\) 可被 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 线性表出, 由引理 3.3.1得 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r},\bm\alpha_l\) 线性相关, 故 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 符合极大无关组的定义.

例 3.3.3: 设 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=r\), 证明: 若 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 可以被其中 \(r\) 个向量 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 线性表出, 则 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 是一个极大无关组.

设 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 是一个极大无关组, 则 \(\mathrm{rank}\{\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\}=r\). 而 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 可被 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 线性表出, 故 \(\mathrm{rank}\{\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\}\leq \mathrm{rank}\{\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\}\).

因此 \(\mathrm{rank}\{\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\}=r\), \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 线性无关, 再由例 3.3.2 得 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 是极大无关组.

例 3.3.4: 在 \(K^n\) 中, 任一线性无关的向量组所含向量数不超过 \(n\).

任一线性无关的 \(\bm\alpha_1,\cdots,\bm\alpha_s\) 都可被 \(\bm\varepsilon_1,\cdots,\bm\varepsilon_n\) 线性表出, 由推论 3.3.3得 \(s\leq n\).

例 3.3.5: 证明: 在 \(K^n\) 中, \(n\) 个向量 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关当且仅当 \(K^n\) 中任一向量都可被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

\((\Rightarrow)\) 若 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 则 \(\forall\bm\beta\in K^n\), 由例 3.2.4得 \(\bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\) 线性相关, 再由命题 3.2.1得 \(\bm\beta\) 可被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

\((\Leftarrow)\) 若 \(K^n\) 中任一向量都可被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 则 \(\bm\varepsilon_1,\cdots,\bm\varepsilon_n\) 可被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 由命题 3.3.3得 \(n=\mathrm{rank}\{\bm\varepsilon_1,\cdots,\bm\varepsilon_n\}\leq \mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}\), 故由命题 3.3.2得 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关.

例 3.3.6: 若 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\}\), 则 \(\bm\beta\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

设 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 是 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的极大无关组, 由例 3.3.2得它也是 \(\bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\) 的极大无关组, 于是 \(\bm\beta\) 可由 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 线性表出, 进而可由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出.

例 3.3.7: 两个向量组等价的充要条件是: 它们的秩相等, 且其中一个向量组可被另一个向量组线性表出.

\((\Rightarrow)\) 显然.

\((\Leftarrow)\) 若两个向量组秩相等, 且 \((I)\) 可被 \((II)\) 线性表出. 设 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 和 \(\bm\beta_1,\cdots,\bm\beta_r\) 分别是 \((I)\) 和 \((II)\) 的极大无关组, 则 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 可被 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性表出.

任取 \(\bm\beta_i\), 则 \(\bm\alpha_1,\cdots,\bm\alpha_r,\bm\beta_i\) 可被 \(\bm\beta_1,\cdots,\bm\beta_r\) 线性表出, 由引理 3.3.1得 \(\bm\alpha_1,\cdots,\bm\alpha_r,\bm\beta_i\) 线性相关, 再由命题 3.2.1得 \(\bm\beta_i\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 线性表出, 因此 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 与 \(\bm\beta_1,\cdots,\bm\beta_r\) 定价, 进而 \((I)\) 和 \((II)\) 等价.

例 3.3.8: 向量组的任何一个线性无关组都可以扩充为极大无关组.

设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的一个线性无关组为 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_m}\). 若 \(m=n\), 则 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_m}\) 就是极大无关组.

若 \(m<n\), 若 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_m}\) 不是极大无关组, 则在其余向量中存在 \(\bm\alpha_{i_{m+1}}\) 使得 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_m},\bm\alpha_{i_{m+1}}\) 线性无关. 如此继续下去, 最终得到 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 是极大无关组.

例 3.3.11: 设矩阵 \(\bm A_{n\times n}=(a_{ij})\), 满足 \(\displaystyle |a_{ii}|>\sum_{j=1,j\neq i}^n|a_{ij}|\). 证明 \(\bm A\) 的列向量组 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 秩为 \(n\).

假如 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关, 则存在不全为 0 的 \(k_1,\cdots,k_n\), 使得 \(k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n=\bm0\).

设 \(|k_i|=\max\{|k_1|,\cdots,|k_n|\}\), 则 \(k_i\neq0\). 于是 \(\bm\alpha_i=-\frac{k_1}{k_i}\bm\alpha_1-\cdots-\frac{k_n}{k_i}\bm\alpha_n\), 考虑第 \(i\) 个分量, 则有

\[a_{ii}=-\frac{k_1}{k_i}a_{i1}-\cdots-\frac{k_n}{k_i}a_{in}=-\sum_{j=1,j\neq i}^n \frac{k_j}{k_i}a_{ij} \]

于是

\[|a_{ii}|<\sum_{j=1,j\neq i}^n\frac{|k_j|}{|k_i|}|a_{ij}|<\sum_{j=1,j\neq i}^n|a_{ij}| \]

矛盾.

习题 3.3.4: 证明: \(n\) 个方程的 \(n\) 元方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm\beta\) 对 \(\forall\bm\beta\in K^n\) 都有解的充要条件是 \(|\bm A|\neq0\).

\((\Rightarrow)\) 若 \(\forall\bm\beta\in K^n\), \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm\beta\) 都有解, 则 \(\bm\beta\) 可被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出,

由例 3.3.5得 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性无关, 故 \(|\bm A|\neq0\).

\((\Leftarrow)\) 由 Cramer 法则可得.

习题 3.3.5: 证明: \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_s,\bm\beta_1,\cdots,\bm\beta_r\}\leq \mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_s\}+\mathrm{rank}\{\bm\beta_1,\cdots,\bm\beta_r\}\).

设 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_u}\) 和 \(\bm\beta_{j_1},\cdots,\bm\beta_{j_v}\) 是极大无关组, 则 \(\bm\alpha_1,\cdots,\bm\alpha_s,\bm\beta_1,\cdots,\bm\beta_r\) 可被 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_u},\bm\beta_{j_1},\cdots,\bm\beta_{j_v}\) 线性表出, 由命题 3.3.3得,

\[\begin{aligned} \mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_s,\bm\beta_1,\cdots,\bm\beta_r\}&\leq\mathrm{rank}\{\bm\alpha_{i_1},\cdots,\bm\alpha_{i_u},\bm\beta_{j_1},\cdots,\bm\beta_{j_v}\}\\ &\leq u+v\\ &=\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_s\}+\mathrm{rank}\{\bm\beta_1,\cdots,\bm\beta_r\} \end{aligned} \]

习题 3.3.6: 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 的每个向量都可被 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 唯一线性表出, 证明 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 是极大无关组.

由例 3.2.6得 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 线性无关, 且 \(\forall \bm\beta\in\{\bm\alpha_1,\cdots,\bm\alpha_n\}\), \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r},\bm\beta\) 都线性相关, 故 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 符合极大无关组的定义.

习题 3.3.7: 设 \(\bm\alpha_1,\cdots,\bm\alpha_4\) 线性无关, \(\bm\beta_1=\bm\alpha_1-\bm\alpha_2\), \(\bm\beta_2=\bm\alpha_2-\bm\alpha_3\), \(\bm\beta_3=\bm\alpha_3-\bm\alpha_4\), \(\bm\beta_4=\bm\alpha_4-\bm\alpha_1\), 求 \(\bm\beta_1,\cdots,\bm\beta_4\) 的极大无关组.

考虑方程组 \(x_1\bm\beta_1+x_2\bm\beta_2+x_3\bm\beta_3+x_4\bm\beta_4=\bm0\),

即 \((x_1-x_4)\bm\alpha_1+(-x_1+x_2)\bm\alpha_2+(-x_2+x_3)\bm\alpha_3+(-x_3+x_4)\bm\alpha_1=\bm0\), 而 \(\bm\alpha_1,\cdots,\bm\alpha_4\) 线性无关, 故

\[\begin{bmatrix}1&0&0&-1\\ -1&1&0&0\\ 0&-1&1&0\\ 0&0&-1&1 \end{bmatrix}\bm x=\bm0 \]

而 \(\begin{bmatrix}1&0&0&-1\\ -1&1&0&0\\ 0&-1&1&0\\ 0&0&-1&1 \end{bmatrix}\sim \begin{bmatrix}1&0&0&-1\\ 0&1&0&-1\\ 0&0&1&-1\\ 0&0&0&0 \end{bmatrix}\), 故 \(\mathrm{rank}\{\bm\beta_1,\cdots,\bm\beta_4\}=3\), 且 \(\bm\beta_1,\bm\beta_2,\bm\beta_3\) 线性无关, 故可以作为极大无关组.

习题 3.3.10: 设 \(\bm\beta\) 可由 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 但无法被 \(\bm\alpha_1,\cdots,\bm\alpha_{n-1}\) 线性表出, 证明 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_{n-1},\bm\beta\}\).

设 \(\bm\beta=k_1\bm\alpha_1+\cdots+k_n\bm\alpha_n\), 其中 \(k_1,\cdots,k_n\) 不全为 0. 于是 \(k_n\neq0\), 否则 \(\bm\beta\) 就可被 \(\bm\alpha_1,\cdots,\bm\alpha_{n-1}\) 线性表出.

所以 \(\bm\alpha_n\) 可被 \(\bm\alpha_1,\cdots,\bm\alpha_{n-1},\bm\beta\) 线性表出. 故 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 和 \(\bm\alpha_1,\cdots,\bm\alpha_{n-1},\bm\beta\) 等价.

基和维度

定义 3.4.1: 设 \(U\) 是 \(K^n\) 的子空间, 若 \(\bm\alpha_1,\cdots,\bm\alpha_r\in U\) 满足:

(1) \(\bm\alpha_1,\cdots,\bm\alpha_r\) 线性无关;

(2) \(U\) 中的任意向量都可被 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 线性表出,

则称 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 为 \(U\) 的一个基.

因为 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 线性无关, 故 \(\forall\bm\beta\in U\), \(\bm\beta\) 用 \(\bm\alpha_1,\cdots,\bm\alpha_r\) 的表出方式都唯一.

定理 3.4.1: \(K^n\) 的任意非零子空间 \(U\) 都存在基.

取 \(U\) 中的一个非零向量 \(\bm a_1\), 若 \(\langle\bm a_1\rangle\neq U\), 则存在 \(\bm a_2\in U\), 使得 \(\bm a_2\notin\langle\bm a_1\rangle\), 于是 \(\bm a_1,\bm a_2\) 线性无关.

若 \(\langle\bm a_1,\bm a_2\rangle\neq U\), 则存在 \(\bm a_3\in U\backslash \langle\bm a_1,\bm a_2\rangle\), 以此类推, 直到 \(\langle\bm a_1,\cdots,\bm a_r\rangle=U\), 则 \(\bm a_1,\cdots,\bm a_r\) 是一组基.

定理 3.4.2: 非零子空间 \(U\) 的任意两个基所含向量数相等.

两组基可以互相线性表出, 故等价. 且两组基都线性无关, 由推论 3.3.4得向量数相等.

定义 3.4.2: 非零子空间 \(U\) 的一个基所含向量数称为 \(U\) 的维度, 记作 \(\dim U\). (定义 \(\dim\{\bm0\}=0\))

\(\forall \bm a\in U\), \(\bm a\) 都可以被 \(U\) 的基唯一线性表出: \(\bm a=a_1\bm a_1+\cdots+a_n\bm a_n\), 称有序数组 \((a_1,\cdots,a_n)\) 为 \(\bm a\) 在基 \(\bm a_1,\cdots,\bm a_n\) 下的坐标.

命题 3.4.1: 设 \(\dim U=r\), 则 \(U\) 中任意 \(r+1\) 个向量都线性相关.

设 \(U\) 的一个基为 \(\bm a_1,\cdots,\bm a_n\), 则任意的 \(r+1\) 个向量组成的向量组都可被这个基线性表出, 由引理 3.3.1得线性相关.

命题 3.4.2: 设 \(\dim U=r\), 则 \(U\) 中任意 \(r\) 个线性无关的向量都可组成一个基.

设 \(\bm a_1,\cdots,\bm a_r\) 线性无关, 由命题 3.4.1 得, \(\forall \bm b\in U\), \(\bm a_1,\cdots,\bm a_r,\bm b\) 线性相关, 再由命题 3.2.1得 \(\bm b\) 可由 \(\bm a_1,\cdots,\bm a_r\) 线性表出, 故 \(\bm a_1,\cdots,\bm a_r\) 是一个基.

命题 3.4.3: 设 \(\dim U=r\), \(\bm a_1,\cdots,\bm a_r\in U\), 若 \(U\) 中的每个向量都可由 \(\bm a_1,\cdots,\bm a_r\) 线性表出, 则 \(\bm a_1,\cdots,\bm a_r\) 是一个基.

取 \(U\) 的一个基 \(\bm\delta_1,\cdots,\bm\delta_r\), 则 \(\bm\delta_1,\cdots,\bm\delta_r\) 可被 \(\bm a_1,\cdots,\bm a_r\) 线性表出, 因而两者等价, 于是 \(\mathrm{rank}\{\bm a_1,\cdots,\bm a_r\}=r\).

再由命题 3.3.2得 \(\bm a_1,\cdots,\bm a_r\) 线性无关, 故是一个基.

命题 3.4.4: 设 \(U,W\) 是 \(K^n\) 的非零子空间, 若 \(U\sube W\), 则 \(\dim U\leq \dim W\).

在 \(U\) 和 \(W\) 中各取一个基 \(\bm a_1,\cdots,\bm a_r\) 和 \(\bm b_1,\cdots,\bm b_s\), 因为 \(U\sube W\), 故 \(\bm a_1,\cdots,\bm a_r\) 可被 \(\bm b_1,\cdots,\bm b_s\) 线性表出,

于是 \(\dim U=r\leq s=\dim W\).

命题 3.4.5: 设 \(U,W\) 是 \(K^n\) 的非零子空间, 且 \(U\sube W\), 若 \(\dim U=\dim W\), 则 \(U=W\).

在 \(U\) 中取一个基 \(\bm a_1,\cdots,\bm a_r\), 因 \(U\sube W\), 故 \(\bm a_1,\cdots,\bm a_r\in W\).

而 \(\dim U=\dim W\), 根据命题 3.4.2得 \(\bm a_1,\cdots,\bm a_r\) 也是 \(W\) 的基, 所以 \(W\sube U\), 进而 \(U=W\).

定理 3.4.3: 向量组 \(\bm a_1,\cdots,\bm a_n\) 的极大无关组是 \(\langle \bm a_1,\cdots,\bm a_n\rangle\) 的一个基, 从而

\[\mathrm{rank}\{\bm a_1,\cdots,\bm a_n\}=\dim\langle\bm a_1,\cdots,\bm a_n\rangle \]

取 \(\bm a_1,\cdots,\bm a_n\) 的极大无关组 \(\bm a_{i_1},\cdots,\bm a_{i_r}\), 由线性表出的传递性知, \(\langle \bm a_1,\cdots,\bm a_n\rangle\) 中任意向量都可被 \(\bm a_{i_1},\cdots,\bm a_{i_r}\) 线性表出, 所以 \(\bm a_{i_1},\cdots,\bm a_{i_r}\) 是 \(\langle \bm a_1,\cdots,\bm a_n\rangle\) 的一个基.

例 3.4.2: 设数域 \(K\) 上的 \(n\) 阶矩阵 \(\bm A\), 证明: 若 \(|\bm A|\neq0\), 则 \(\bm A\) 的列向量组 \(\bm a_1,\cdots,\bm a_n\) 是 \(K^n\) 的基.

因为 \(|\bm A|\neq0\), 故 \(\bm a_1,\cdots,\bm a_n\) 线性无关, 由命题 3.4.2得 \(\bm a_1,\cdots,\bm a_n\) 是 \(K^n\) 的基.

矩阵的秩

矩阵 \(\bm A\) 的列向量组的秩称为列秩, 行向量组的秩称为行秩.

定理 3.5.1: 阶梯形矩阵 \(\bm J\) 的行秩和列秩相等, 都等于 \(\bm J\) 中非零行的个数. \(\bm J\) 的主元所在的列构成列向量组的极大无关组.

设 \(\bm J_{n\times m}\) 有 \(r\) 个非零行, 主元分别位于第 \(j_1,\cdots,j_r\) 列:

\[\bm J=\begin{bmatrix} 0&\cdots&0&c_{1j_1}&\cdots&c_{1j_2}&\cdots&c_{1j_r}&\cdots&c_{1n}\\0&\cdots&0&0&\cdots&c_{2j_2}&\cdots&c_{2j_r}&\cdots&c_{2n}\\ \vdots&&\vdots&\vdots&&\vdots&&\vdots&&\vdots\\0&\cdots&0&0&\cdots&0&\cdots&c_{nj_r}&\cdots&c_m\\0&\cdots&0&0&\cdots&0&\cdots&0&\cdots&0\\ \vdots&&\vdots&\vdots&&\vdots&&\vdots&&\vdots\\0&\cdots&0&0&\cdots&0&\cdots&0&\cdots&0 \end{bmatrix} \]

设列向量组为 \(\bm\alpha_1,\cdots,\bm\alpha_n\), 行向量组为 \(\bm\beta_1,\cdots,\bm\beta_m\).

先求 \(\bm J\) 的列秩. 因为下述向量组线性无关

\[\begin{pmatrix}c_{1j_1}\\0\\ \vdots\\0\end{pmatrix}, \begin{pmatrix}c_{1j_2}\\c_{2j_2}\\ \vdots\\0\end{pmatrix}, \cdots, \begin{pmatrix}c_{1j_r}\\c_{2j_r}\\ \vdots\\c_{nj_r}\end{pmatrix} \]

故它的延伸组 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 也线性无关, 于是 \(\mathrm{rank}\{\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\}=r\).

设 \(U=\{(a_1,\cdots,a_r,0,\cdots,0):a_i\in K\}\), 则 \(\dim U=r\).

因为 \(\bm\alpha_1,\cdots,\bm\alpha_n\in U\), 故 \(\langle\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\rangle \sube \langle\bm\alpha_{1},\cdots,\bm\alpha_{n}\rangle \sube U\), 于是

\[r=\dim\langle\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\rangle \leq\dim \langle\bm\alpha_{1},\cdots,\bm\alpha_{n}\rangle \leq \dim U=r \]

所以 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_n\}=\dim \langle\bm\alpha_{1},\cdots,\bm\alpha_{n}\rangle=r\), 且由例 3.3.2得 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\) 就是极大无关组.

再求 \(\bm J\) 的行秩. 因为下述向量组线性无关

\[(c_{1j_1},c_{1j_2},\cdots,c_{1j_r}),(0,c_{2j_2},\cdots,c_{2j_r}),\cdots,(0,0,\cdots,c_{rj_r}) \]

所以其延伸组 \(\bm\beta_1,\cdots,\bm\beta_r\) 也线性无关. 有因 \(\bm\beta_{r+1}=\cdots=\bm\beta_m=\bm0\), 故 \(\bm\beta_1,\cdots,\bm\beta_r\) 是极大无关组, 进而 \(\bm J\) 的行秩为 \(r\).

定理 3.5.2: 矩阵的初等行变换不改变矩阵的行秩.

易得矩阵的行向量组与初等行变换后的行向量组互相等价.

定理 3.5.3: 矩阵的初等行变换不改变列向量组的线性相关性, 因而不改变列秩, 即:

设 \(\bm A\) 经初等行变换得到 \(\bm B\),

(1) \(\bm A\) 的列向量组线性相关当且仅当 \(\bm B\) 的列向量组线性相关.

(2) 若 \(\bm B\) 的第 \(j_1,\cdots,j_r\) 列构成 \(\bm B\) 列向量组的极大无关组, 则 \(\bm A\) 的第 \(j_1,\cdots,j_r\) 列也构成 \(\bm A\) 列向量组的极大无关组.

设 \(\bm A\) 的列向量组为 \(\bm\alpha_1,\cdots,\bm\alpha_n\), \(\bm B\) 的列向量组为 \(\bm\beta_1,\cdots,\bm\beta_n\).

(1) 经过初等行变换后, 齐次方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0\) 与 \(x_1\bm\beta_1+\cdots+x_n\bm\beta_n=\bm0\) 仍同解,

所以一个方程组有非零解当且仅当另一方程组有非零解, 因而 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性相关当且仅当 \(\bm\beta_1,\cdots,\bm\beta_n\) 线性相关.

(2) 设 \(\bm A\) 和 \(\bm B\) 的第 \(j_1,\cdots,j_r\) 列分别组成新矩阵 \(\bm A'\) 和 \(\bm B'\), 则 \(\bm A'\) 经过相同的初等行变换变成 \(\bm B'\).

因为 \(\bm B'\) 线性无关, 由 (1) 得 \(\bm A'\) 也线性无关. 再取第 \(j_1,\cdots,j_r,l\) 列组成 \(\bm A''\) 和 \(\bm B''\), 因为 \(\bm B''\) 线性相关, 故 \(\bm A''\) 也线性相关, 于是 \(\bm A\) 的第 \(j_1,\cdots,j_r\) 列构成 \(\bm A\) 列向量组的极大无关组.

定理 3.5.4: 任意矩阵 \(\bm A\) 的行秩和列秩都相等.

将 \(\bm A\) 经初等行变换变成阶梯形矩阵 \(\bm J\), 再由定理 3.5.1和定理 3.5.3可得.

定义 3.5.1: 矩阵 \(\bm A\) 的行秩和列秩统称为 \(\bm A\) 的秩.

推论 3.5.1: 设 \(\bm A\) 经初等行变换变为 \(\bm J\), 则 \(\mathrm{rank}(\bm A)\) 等于 \(\bm J\) 中非零行个数, 设 \(\bm J\) 主元所在的列为 \(j_1,\cdots,j_r\), 则 \(\bm A\) 的第 \(j_1,\cdots,j_r\) 列构成极大无关组.

由定理 3.5.1和定理 3.5.3可得. 此推论给出了求 \(\bm A\) 的秩和极大无关组的一般方法.

推论 3.5.2: 矩阵的初等列变换不改变矩阵的秩.

对 \(\bm A\) 作初等列变换就是对 \(\bm A^T\) 作初等行变换.

定理 3.5.5: 任意非零矩阵的秩等于它不为零的子式的最高阶数.

设 \(\mathrm{rank}(\bm A)=r\), 则对 \(s>r\), 任意的 \(s\) 阶子式 \(A\begin{pmatrix}k_1,k_2,\cdots,k_s\\ l_1,l_2,\cdots,l_s \end{pmatrix}\) 的列向量组都是 \(\bm A\) 第 \(l_1,\cdots,l_s\) 列的缩短组, 于是线性相关, 进而 \(s\) 阶子式为 0.

推论 3.5.3: 设 \(\mathrm{rank}(\bm A)=r\), 则 \(\bm A\) 的不为零的 \(r\) 阶子式所在列(行)构成列(行)向量组的极大无关组.

\(\bm A\) 的不为零的 \(r\) 阶子式的列向量组线性无关, 其延伸组, 即 \(\bm A\) 的对应列线性无关. 而 \(\mathrm{rank}(\bm A)=r\), 故这 \(r\) 列构成列向量组的极大无关组.

推论 3.5.4: \(n\) 阶方阵 \(\bm A\) 满秩的充要条件是 \(|\bm A|\neq0\).

由定理 3.5.5 可得.

例 3.5.6: 证明: 若 \(\mathrm{rank}(\bm A_{n\times m})=r\), 则对 \(\bm A\) 的任意 \(s\) 行组成的子矩阵 \(\bm A_1\), 有 \(\mathrm{rank}(\bm A_1)\geq r+s-n\).

设 \(\mathrm{rank}(\bm A_1)=k\), 取 \(\bm A_1\) 行向量组的极大无关组 \(\bm\beta_{i_1},\cdots,\bm\beta_{i_k}\), 将其扩充为 \(\bm A\) 行向量组的极大无关组 \(\bm\beta_{i_1},\cdots,\bm\beta_{i_k},\bm\beta_{i_{k+1}},\cdots,\bm\beta_{i_r}\),

则 \(\bm\beta_{i_{k+1}},\cdots,\bm\beta_{i_r}\) 不属于 \(\bm A_1\), 而属于 \(\bm A\) 的余下 \(n-s\) 行, 因此 \(r-k\leq n-s\).

例 3.5.7: 设 \(\bm A_{s\times n}\), \(\bm B_{s\times m}\), 用 \((\bm A,\bm B)\) 表示两个矩阵合并得到的 \(s\times(n+m)\) 矩阵, 证明: \(\mathrm{rank}((\bm A,\bm B))=\mathrm{rank}(\bm A)\) 当且仅当 \(\bm B\) 的列向量可以被 \(\bm A\) 的列向量线性表出.

设 \(\bm A\) 和 \(\bm B\) 的列向量组分别为 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 和 \(\bm\beta_1,\cdots,\bm\beta_m\), 则

\[\begin{aligned}&\mathrm{rank}(\bm{A})=\operatorname{rank}((\bm{A},\bm{B}))\\ \overset{命题 3.4.4}{\Longleftrightarrow}& \dim\langle\bm{\alpha}_1,\bm{\alpha}_2,\cdots,\bm{\alpha}_n\rangle=\dim\langle\bm{\alpha}_1,\cdots,\bm{\alpha}_n,\bm{\beta}_1,\cdots,\bm{\beta}_m\rangle\\ \overset{命题3.4.5}{\Longleftrightarrow}& \langle\bm{\alpha}_1,\bm{\alpha}_2,\cdots,\bm{\alpha}_n\rangle=\langle\bm{\alpha}_1,\cdots,\bm{\alpha}_n,\bm{\beta}_1,\cdots,\bm{\beta}_m\rangle\\ \Longleftrightarrow& \bm{\beta}_1,\bm{\beta}_2,\cdots,\bm{\beta}_m\in\langle\bm{\alpha}_1,\bm{\alpha}_2,\cdots,\bm{\alpha}_n\rangle\\ \Longleftrightarrow& \bm{B}\text{ 的列向量组可以由 A 的列向量组线性表出。}\end{aligned} \]

一般地, 由习题 3.3.5得: \(\mathrm{rank}((\bm A,\bm B))\leq \mathrm{rank}(\bm A)+\mathrm{rank}(\bm B)\).

例 3.5.8: 证明

\[\mathrm{rank}\begin{bmatrix}\bm A&\bm0\\ \bm0&\bm B\end{bmatrix}=\mathrm{rank}(\bm A)+\mathrm{rank}(\bm B) \]

作初等行变换:

\[\begin{bmatrix}\bm A&\bm0\\ \bm0&\bm B\end{bmatrix} \rightarrow \begin{bmatrix}\bm J_r&\bm0\\ \bm0&\bm0 \\ \bm0&\bm J_t\\ \bm0&\bm0\end{bmatrix}\rightarrow \begin{bmatrix}\bm J_r&\bm0\\ \bm0&\bm J_t\\ \bm0&\bm0 \\ \bm0&\bm0\end{bmatrix} \]

化成阶梯形矩阵, 故 \(\mathrm{rank}\begin{bmatrix}\bm A&\bm0\\ \bm0&\bm B\end{bmatrix}=r+t=\mathrm{rank}(\bm A)+\mathrm{rank}(\bm B)\).

例 3.5.9: 证明

\[\mathrm{rank}\begin{bmatrix}\bm A&\bm C\\ \bm0&\bm B\end{bmatrix}\geq\mathrm{rank}(\bm A)+\mathrm{rank}(\bm B) \]

设 \(\mathrm{rank}(\bm A)=r\), \(\mathrm{rank}(\bm B)=s\), 则 \(\bm A\) 存在一个 \(r\) 阶子式 \(|\bm A_r|\neq0\), \(\bm B\) 存在一个 \(s\) 阶子式 \(|\bm B_s|\neq0\),

于是 \(\mathrm{rank}\begin{bmatrix}\bm A&\bm C\\ \bm0&\bm B\end{bmatrix}\) 存在一个 \(r+s\) 阶子式 \(\begin{vmatrix}\bm A_r&\bm C_{r\times s}\\ \bm0&\bm B_s\end{vmatrix}=|\bm A_r||\bm B_s|\neq0\),

由定理 3.5.5得 \(\mathrm{rank}\begin{bmatrix}\bm A&\bm C\\ \bm0&\bm B\end{bmatrix}\geq r+s=\mathrm{rank}(\bm A)+\mathrm{rank}(\bm B)\).

线性方程组有解的充要条件

定理 3.6.1: 数域 \(K\) 上的线性方程组 \(x_1\bm\alpha_1+x_2\bm\alpha_2+\cdots+x_n\bm\alpha_n=\bm\beta\) 有解的充要条件是: 系数矩阵和增广矩阵的秩相等.

\[\begin{aligned} &方程组有解\\ \Longleftrightarrow& \bm\beta\in\langle \bm\alpha_1,\cdots,\bm\alpha_n\rangle\\ \Longleftrightarrow& \langle \bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\rangle \sube \langle \bm\alpha_1,\cdots,\bm\alpha_n\rangle\\ \Longleftrightarrow& \langle \bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\rangle = \langle \bm\alpha_1,\cdots,\bm\alpha_n\rangle\\ \overset{命题3.4.5}{\Longleftrightarrow}& \dim\langle \bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta\rangle = \dim\langle \bm\alpha_1,\cdots,\bm\alpha_n\rangle\\ \Longleftrightarrow& \mathrm{rank}( \bm\alpha_1,\cdots,\bm\alpha_n,\bm\beta) =\mathrm{rank}( \bm\alpha_1,\cdots,\bm\alpha_n) \end{aligned} \]

定理 3.6.2: 设 \(n\) 元方程组 \(x_1\bm\alpha_1+x_2\bm\alpha_2+\cdots+x_n\bm\alpha_n=\bm\beta\) 有解, 若 \(\mathrm{rank}(\bm A)=n\), 则有唯一解, 若 \(\mathrm{rank}(\bm A)<n\), 则有无穷解.

推论 3.6.1: \(n\) 元齐次方程组有非零解的充要条件是 \(\mathrm{rank}(\bm A)<n\).

例 3.6.5: 方程组

\[\begin{cases}a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1\\a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2\\ \quad\vdots\\a_{s1}x_1+a_{s2}x_2+\cdots+a_{sn}x_n=b_s\end{cases} \]

有解的充分必要条件是下述方程组：

\[\begin{cases}a_{11}x_1+a_{21}x_2+\cdots+a_{s1}x_s=0\\a_{12}x_1+a_{22}x_2+\cdots+a_{s2}x_s=0\\ \quad\vdots\\a_{1n}x_1+a_{2n}x_2+\cdots+a_{sn}x_s=0\\b_1x_1+b_2x_2+\cdots+b_sx_s=1\end{cases} \]

无解.

设两个方程组的系数矩阵和增广矩阵分别为 \(\bm A,\widetilde{\bm A}\) 和 \(\bm B,\widetilde{\bm B}\), \(\bm\beta=(b_1,\cdots,b_s)^T\), 则

\[\bm B=\widetilde{\bm A}^T,\quad \widetilde{\bm B}=\begin{bmatrix}\bm A^T &\bm0\\ \bm\beta^T &1 \end{bmatrix} \]

设 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r}\) 是 \(\bm A^T\) 行向量组的极大无关组, 因 \(\widetilde{\bm B}\) 的最后一行无法被 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r}\) 线性表出, 故 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r},(\bm\beta^T,1)\) 是 \(\widetilde{\bm B}\) 行向量组的极大无关组, 于是 \(\mathrm{rank}(\widetilde{\bm B})=\mathrm{rank}(\bm A)+1\).

方程组 (1) 有解 \(\Longleftrightarrow\) \(\mathrm{rank}(\bm A)=\mathrm{rank}(\widetilde{\bm A})\) \(\Longleftrightarrow\) \(\mathrm{rank}(\widetilde{\bm B})-1=\mathrm{rank}(\bm B)\) \(\Longleftrightarrow\) 方程组 (2) 无解.

齐次线性方程组解集的结构

设齐次方程组 \(x_1\bm\alpha_1+x_2\bm\alpha_2+\cdots+x_n\bm\alpha_n=\bm0\) 的解集为 \(W\), 它的性质有:

性质 1: 若 \(\bm\gamma,\bm\delta\in W\), 则 \(\bm\gamma+\bm\delta \in W\).

性质 2: 若 \(\bm\gamma\in W\), \(k\in K\), 则 \(k\bm\gamma\in W\).

于是 \(W\) 是 \(K^n\) 的一个子空间, 称其为方程组的解空间. 若系数矩阵 \(\mathrm{rank}(\bm A)=n\), 则 \(W=\{\bm0\}\). 若 \(\mathrm{rank}(\bm A)<n\), 则 \(W\) 非零子空间, 此时把 \(W\) 的基称为方程组的基础解系.

定义 3.7.1: 齐次方程组有非零解时, 若 \(\bm\eta_1,\cdots,\bm\eta_t\) 满足

(1) \(\bm\eta_1,\cdots,\bm\eta_t\) 线性无关;

(2) 方程组的任意解都可被 \(\bm\eta_1,\cdots,\bm\eta_t\) 线性表出,

则称 \(\bm\eta_1,\cdots,\bm\eta_t\) 是齐次方程组的一个基础解系.

若找到了一个基础解系 \(\bm\eta_1,\cdots,\bm\eta_t\), 则 \(W=\langle \bm\eta_1,\cdots,\bm\eta_t\rangle\), 方程组的全部解为 \(k_1\bm\eta_1+\cdots+k_t\bm\eta_t\), \(k_i\in K\).

定理 3.7.1: \(\dim W=n-\mathrm{rank}(\bm A)\).

若 \(\mathrm{rank}(\bm A)=n\), 则 \(\dim W=\{\bm0\}\). 若 \(\mathrm{rank}(\bm A)=r\),

对 \(\bm A\) 作初等行变换变为简化行阶梯形矩阵 \(\bm J\), 则 \(\bm J\) 有 \(r\) 个主元, 设它们在前 \(r\) 列, 故方程的一般解为

\[\left\{\begin{aligned} &x_1=-b_{1,r+1}x_{r+1}-\cdots-b_{1n}x_n\\ &x_2=-b_{2,r+1}x_{r+1}-\cdots-b_{2n}x_n\\ &\quad\vdots\\ &x_r=-b_{n,r+1}x_{r+1}-\cdots-b_{nn}x_n \end{aligned}\right. \tag{1} \]

令自由未知量分别取以下值:

\[\begin{pmatrix}x_{r+1}\\ x_{r+2}\\ \vdots\\ x_n \end{pmatrix} =\begin{pmatrix}1\\0\\ \vdots\\0 \end{pmatrix}, \begin{pmatrix}0\\1\\ \vdots\\0 \end{pmatrix},\cdots, \begin{pmatrix}1\\0\\ \vdots\\1 \end{pmatrix} \tag{2} \]

得到方程组的 \(n-r\) 个解:

\[\bm\eta_1=\begin{pmatrix}-b_{1,r+1}\\ -b_{2,r+1}\\ \vdots\\ -b_{n,r+1}\\ 1\\0\\ \vdots\\ 0 \end{pmatrix}, \bm\eta_2=\begin{pmatrix}-b_{1,r+2}\\ -b_{2,r+2}\\ \vdots\\ -b_{n,r+2}\\ 0\\1\\ \vdots\\ 0 \end{pmatrix},\cdots, \bm\eta_{n-r}=\begin{pmatrix}-b_{1,n}\\ -b_{2,n}\\ \vdots\\ -b_{n,n}\\ 0\\0\\ \vdots\\ 1 \end{pmatrix} \]

向量组 \(\bm\eta_1,\cdots,\bm\eta_{n-r}\) 是 (2) 的延伸组, 因此线性无关. 任取一个解 \(\bm\eta=(c_1,c_2,\cdots,c_n)^T\), 它满足一般解公式 (1), 即

\[\left\{\begin{aligned} &c_1=-b_{1,r+1}c_{r+1}-\cdots-b_{1n}c_n\\ &c_2=-b_{2,r+1}c_{r+1}-\cdots-b_{2n}c_n\\ &\quad\vdots\\ &c_r=-b_{n,r+1}c_{r+1}-\cdots-b_{nn}c_n \end{aligned}\right. \]

于是

\[\bm\eta=\begin{pmatrix}-b_{1,r+1}c_{r+1}-\cdots-b_{1n}c_n\\ -b_{2,r+1}c_{r+1}-\cdots-b_{2n}c_n\\ \vdots\\ -b_{n,r+1}c_{r+1}-\cdots-b_{nn}c_n\\ c_{r+1}\\ \vdots\\ c_n \end{pmatrix}= c_{r+1}\bm\eta_1+\cdots+c_n\bm\eta_{n-r} \]

即每个解都可被 \(\bm\eta_1,\cdots,\bm\eta_{n-r}\) 线性表出, 因此 \(\bm\eta_1,\cdots,\bm\eta_{n-r}\) 是一个基础解系, 所以 \(\dim W=n-r\).

例 3.7.3: 设 \(n\) 个方程的 \(n\) 元齐次方程组, 其系数矩阵 \(|\bm A|=0\), 且 \((k,l)\) 元的代数余子式 \(A_{kl}\neq0\), 证明: \(\bm\eta=(A_{k1},\cdots,A_{kn})^T\) 是一个基础解系.

\(\bm A\) 有一个 \(n-1\) 阶子式 \(A_{kl}\neq0\), 且 \(|\bm A|=0\), 所以 \(\mathrm{rank}(\bm A)=n-1\). 故齐次方程组解空间 \(W\) 的维度是 \(\dim W=n-(n-1)=1\).

考虑方程组的第 \(i\) 个方程: \(a_{i1}x_1+\cdots+a_{in}x_n=0\), 代入 \(\bm\eta=(A_{k1},\cdots,A_{kn})^T\),

若 \(i\neq k\), 则 \(a_{i1}A_{k1}+\cdots+a_{in}A_{kn}=0\); 若 \(i=k\), 则 \(a_{k1}A_{k1}+\cdots+a_{kn}A_{kn}=|\bm A|=0\).

于是 \(\bm\eta=(A_{k1},\cdots,A_{kn})^T\) 是方程组的一个非零解, 于是也是一个基础解系.

例 3.7.5: 设 \(\bm A_1\) 是 \(\bm A_{s\times n}\) 的前 \(s-1\) 行组成的子矩阵, 证明: 若以 \(\bm A_1\) 为系数矩阵的齐次方程组的解都满足 \(a_{s1}x_1+\cdots+a_{sn}x_n=0\), 则 \(\bm A\) 的第 \(s\) 行可由前 \(s-1\) 行线性表出.

可以看出, 以 \(\bm A_1\) 和 \(\bm A\) 为系数矩阵的齐次方程组同解, 即解空间 \(W\) 相同. 因 \(\dim W=n-\mathrm{rank}(\bm A)=n-\mathrm{rank}(\bm A_1)\), 所以 \(\mathrm{rank}(\bm A)=\mathrm{rank}(\bm A_1)\).

设 \(\bm A\) 的行向量组为 \(\bm\alpha_1,\cdots,\bm\alpha_s\), 于是 \(\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_{s-1},\bm\alpha_s\}=\mathrm{rank}\{\bm\alpha_1,\cdots,\bm\alpha_{s-1}\}\), 由例 3.3.6得 \(\bm\alpha_s\) 可被 \(\bm\alpha_1,\cdots,\bm\alpha_{s-1}\) 线性表出.

例 3.7.6: 设 \(\bm A_{s\times n}=(a_{ij})\) 的秩 \(\mathrm{rank}(\bm A)=r\), 以 \(\bm A\) 为系数矩阵的齐次方程组的一个基础解系为:

\[\bm{\eta}_1=\begin{pmatrix}b_{11}\\b_{12}\\ \vdots\\b_{1n}\end{pmatrix}, \bm{\eta}_2=\begin{pmatrix}b_{21}\\b_{22}\\ \vdots\\b_{2n}\end{pmatrix}, \cdots, \bm{\eta}_{n-r}=\begin{pmatrix}b_{n-r,1}\\b_{n-r,2}\\ \vdots\\b_{n-r,n}\end{pmatrix} \]

设 \(\bm B\) 是以 \(\bm\eta_1^T,\cdots,\bm\eta_{n-r}^T\) 为行向量组的 \((n-r)\times n\) 矩阵, 求以 \(\bm B\) 为系数矩阵的齐次方程组的基础解系.

\(\bm B\) 的行向量组线性无关, 故 \(\mathrm{rank}(\bm B)=n-r\), 设以 \(\bm B\) 为系数矩阵的齐次方程组的解空间为 \(W\), 则 \(\dim W=r\).

将 \(\bm\eta_j\) 代入以 \(\bm A\) 为系数矩阵的齐次方程组得: \(\forall i\in\{1,\cdots,s\}\), \(a_{i1}b_{j1}+\cdots+a_{in}b_{jn}=0\), \(j=1,\cdots,n-r\).

故 \((a_{i1},\cdots,a_{in})^T\) 就是以 \(\bm B\) 为系数矩阵的齐次方程组的一个解.

取 \(\bm A\) 行向量组的极大无关组 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\), 则 \(\bm\alpha_{i_1}^T,\cdots,\bm\alpha_{i_r}^T\) 就是以 \(\bm B\) 为系数矩阵的齐次方程组的基础解系.

非齐次线性方程组解集的结构

设 \(n\) 元非齐次方程组 \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm\beta\) 的解集为 \(U\), 对应的齐次方程组(导出组) \(x_1\bm\alpha_1+\cdots+x_n\bm\alpha_n=\bm0\) 的解集为 \(W\). 解集 \(U\) 有如下性质:

性质 1: 若 \(\bm\gamma,\bm\delta\in U\), 则 \(\bm\gamma-\bm\delta\in W\).

性质 2: 若 \(\bm\gamma\in U\), \(\bm\delta\in W\), 则 \(\bm\gamma+\bm\delta\in U\).

定理 3.8.1: 若数域 \(K\) 上的 \(n\) 元非齐次方程组有解, 则它的解集为

\[U=\{\bm\gamma_0+\bm\eta:\bm\eta\in W\} \]

其中 \(\bm\gamma_0\) 是非齐次方程组的一个解(特解), \(W\) 是导出组的解空间.

设解集为 \(U'\), 令 \(U=\{\bm\gamma_0+\bm\eta:\bm\eta\in W\}\).

\(\forall \bm\eta\in W\), 由性质 2 得 \(\bm\gamma_0+\bm\eta\in U'\), 故 \(U\sube U'\);

另外 \(\forall \bm\gamma\in U'\), 由性质 1 得 \(\bm\gamma-\bm\gamma_0\in W\), 即 \(\bm\gamma=\bm\gamma_0+(\bm\gamma-\bm\gamma_0)\in U\), 故 \(U'\sube U\). 于是 \(U'=U\).

把 \(\{\bm\gamma_0+\bm\eta:\bm\eta\in W\}\) 记为 \(\bm\gamma_0+W\), 称它为一个 \(W\) 型的线性流形. 注意 \(U\) 不是 \(K^n\) 的子空间, 它对加法和数乘运算不封闭.

推论 3.8.1: \(n\) 元非齐次方程组有唯一解的充要条件是: 它的导出组只有零解.

非齐次方程组有唯一解 \(\Longleftrightarrow\) \(U=\bm\gamma_0+W=\{\bm\gamma_0\}\) \(\Longleftrightarrow\) \(W=\{\bm0\}\).

当非齐次方程组有无穷解时, 它的导出组必有非零解, 取导出组的基础解系 \(\bm\eta_1,\cdots,\bm\eta_{n-r}\), 则解集 \(U\) 为:

\[U=\{\bm\gamma_0+k_1\bm\eta_1+\cdots+k_{n-r}\bm\eta_{n-r}:k_i\in K\} \]

解非齐次方程组一般步骤: 令自由未知量取 0, 得到特解, 再解出导出组的基础解系, 就可得到 \(U\).

例 3.8.2: 设 \(\bm\gamma_0\) 是非齐次方程组的特解, \(\bm\eta_1,\cdots,\bm\eta_{n-r}\) 是导出组的基础解系, 令 \(\bm\gamma_i=\bm\gamma_0+\bm\eta_i\), \(i=1,\cdots,n-r\). 证明解集为:

\[U=\Big\{u_0\bm\gamma_0+u_1\bm\gamma_1+\cdots+u_{n-r}\bm\gamma_{n-r}:\sum_{i=0}^{n-r}u_i=1\Big\} \]

设解集为 \(U'\), 则 \(\forall \bm\delta\in U\), \(\bm\delta=u_0\bm\gamma_0+u_1\bm\gamma_1+\cdots+u_{n-r}\bm\gamma_{n-r}=\gamma_0+u_1\bm\eta_1+\cdots+u_{n-r}\bm\eta_{n-r}\in U'\);

\(\forall\bm\delta\in U'\), 存在 \(k_1,\cdots,k_{n-r}\in K\), 使 \(\bm\delta=\bm\gamma_0+k_1\bm\eta_1+\cdots+k_{n-r}\bm\eta_{n-r}=(1-k_1-\cdots-k_{n-r})\bm\gamma_0+k_1\bm\gamma_1+\cdots+k_{n-r}\bm\gamma_{n-r}\in U\). 于是 \(U'=U\).

例 3.8.3: 求 \(n\) 个平面 \(a_ix+b_iy+c_iz+d_i=0\) (\(i=1,\cdots,n\)) 通过同一直线但不重合的充分必要条件.

通过同一直线但不重合 \(\Longleftrightarrow\) 三元方程组有解, 解集为一维线性流形 \(\Longleftrightarrow\) 三元方程组有解, 导出组的系数矩阵秩为 2 \(\Longleftrightarrow\) \(\mathrm{rank}(\bm A)=\mathrm{rank}(\widetilde{\bm A})=2\).

例 3.8.4: 讨论三个平面的所有可能位置关系

\[a_1x+b_1y+c_1z+d_1=0 \\a_2x+b_2y+c_2z+d_2=0 \\a_3x+b_3y+c_3z+d_3=0 \]

设 \(\bm A\) 和\(\widetilde{\bm A}\) 分别为系数矩阵和增广矩阵, 行向量组为 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\).

(1) \(\mathrm{rank}(\bm A)=\mathrm{rank}(\widetilde{\bm A})=1\). 此时 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 成比例, 解集为二维线性流形, 即三个平面重合.

(2) \(\mathrm{rank}(\bm A)=\mathrm{rank}(\widetilde{\bm A})=2\). 此时解集为一维线性流形. 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 两两不成比例, 则三个平面过同一直线; 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 有两个成比例, 则其中两个平面重合, 另一平面与它们相交.

(3) \(\mathrm{rank}(\bm A)=\mathrm{rank}(\widetilde{\bm A})=3\). 此时有唯一解, 三个平面交于同一点.

(4) \(\mathrm{rank}(\bm A)=1,\mathrm{rank}(\widetilde{\bm A})=2\). 此时三个平面没有公共点. 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 两两不成比例, 则三个平面平行; 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 有两个成比例, 则有两个平面重合, 另一平面与它们平行.

(5) \(\mathrm{rank}(\bm A)=2,\mathrm{rank}(\widetilde{\bm A})=3\). 此时三个平面没有公共点. 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 两两不成比例, 则两两相交; 若 \(\bm\gamma_1,\bm\gamma_2,\bm\gamma_3\) 有两个成比例, 则有两个平面平行, 另一平面与它们相交.

线性方程组在几何上的应用

例 3.9.1: 求平面上三点 \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) 共线的充要条件.

设 \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) 都位于直线 \(ax+by+c=0\) 上, 则

\[\begin{cases}ax_1+by_1+c=0\\ ax_2+by_2+c=0\\ ax_3+by_3+c=0\end{cases} \]

三点共线 \(\Longleftrightarrow\) 以 \(a,b,c\) 为未知量的方程组有非零解 \(\Longleftrightarrow\) \(\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}=0\).

例 3.9.2: 求平面上 \(n\) 个点 \((x_1,y_1),\cdots,(x_n,y_n)\) 共线的充要条件.

类似于例 3.9.1, \(n\) 点共线 \(\Longleftrightarrow\) \(\begin{pmatrix}x_1&y_1&1\\x_2&y_2&1\\ \vdots&\vdots&\vdots\\x_n&y_n&1\end{pmatrix}\) 的秩小于 3.

例 3.9.3: 求空间内四点 \((x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3),(x_4,y_4,z_4)\) 共面的充要条件.

四点共面 \(\Longleftrightarrow\) \(\begin{vmatrix}x_1&y_1&z_1&1\\x_2&y_2&z_2&1\\x_3&y_3&z_3&1\\x_4&y_4&z_4&1\end{vmatrix}=0\).

例 3.9.4 求不共线的四点 \((x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4)\) 在同一圆上的充要条件.

设圆方程为 \(a(x^2+y^2)+bx+cy+d=0\).

四点共圆 \(\Longleftrightarrow\) \(\begin{cases}a(x_1^2+y_1^2)+bx_1+cy_1+d=0\\a(x_2^2+y_2^2)+bx_2+cy_2+d=0\\ a(x_3^2+y_3^2)+bx_3+cy_3+d=0\\ a(x_4^2+y_4^2)+bx_4+cy_4+d=0\end{cases}\) 有非零解 \(\Longleftrightarrow\) \(\begin{vmatrix}x_1^2+y_1^2&x_1&y_1&1\\x_2^2+y_2^2&x_2&y_2&1\\x_3^2+y_3^2&x_3&y_3&1\\x_4^2+y_4^2&x_4&y_4&1\end{vmatrix}=0\).

注意四点不共线, \(\begin{cases}bx_1+cy_1+d=0\\ bx_2+cy_2+d=0\\ bx_3+cy_3+d=0\\ bx_4+cy_4+d=0\end{cases}\) 只有零解, 这保证了 \(a\neq0\).

例 3.9.5: 求不共线的三点 \((x_1,y_1),(x_2,y_2),(x_3,y_3)\) 所确定的圆的方程.

设 \(M(x,y)\) 点在此圆上, 则 \(\begin{vmatrix}x^2+y^2&x&y&1\\x_1^2+y_1^2&x_1&y_1&1\\x_2^2+y_2^2&x_2&y_2&1\\x_3^2+y_3^2&x_3&y_3&1\end{vmatrix}=0\) 就是圆的方程.

例 3.9.8: 求五点 \((x_1,y_1),(x_2,y_2),(x_3,y_3),(x_4,y_4),(x_5,y_5)\) 所确定的二次曲线方程.

设二次曲线方程为 \(ax^2+bxy+cy^2+dx+cy+f=0\), 则

\(\begin{vmatrix}x^2&xy&y^2&x&y&1\\ x_1^2&x_1y_1&y_1^2&x_1&y_1&1\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ x_5^2&x_5y_5&y_5^2&x_5&y_5&1 \end{vmatrix}=0\) 就是二次曲线的方程, 且代数余子式 \(A_{11},A_{12},A_{13}\) 不全为 0.

矩阵的运算

矩阵的加法, 数乘和乘法

设 \(\bm A=(a_{ij})_{n\times m}\), \(\bm B=(b_{ij})_{n\times m}\).

加法: \(\bm A+\bm B=(a_{ij}+b_{ij})\).

数乘: \(k\bm A=(ka_{ij})\).

若 \(\bm A=(a_{ij})_{s\times n}\), \(\bm B=(b_{ij})_{n\times m}\),

乘法: \(\bm C=\bm A\bm B=(c_{ij})\), 其中 \(c_{ij}=\displaystyle \sum_{k=1}^n a_{ik}b_{kj}\).

(1) 乘法符合结合律: \((\bm A\bm B)\bm C=\bm A(\bm B\bm C)\).

设 \(\bm A=(a_{ij})_{s\times n}\), \(\bm B=(b_{ij})_{n\times m}\), \(\bm C=(c_{ij})_{m\times r}\), 则

\([\displaystyle (\bm A\bm B)\bm C]_{(i,j)}=\sum_{k=1}^m [\bm A\bm B]_{(i,k)}c_{kj}=\sum_{k=1}^m c_{kj} \sum_{t=1}^n a_{it}b_{tk}=\sum_{k=1}^m \sum_{t=1}^n a_{it}b_{tk}c_{kj}\),

\(\displaystyle [\bm A(\bm B\bm C)]_{(i,j)}=\sum_{t=1}^n a_{it}[\bm B\bm C]_{(t,j)}=\sum_{t=1}^na_{it} \sum_{k=1}^m b_{tk}c_{kj}= \sum_{k=1}^m \sum_{t=1}^n a_{it}b_{tk}c_{kj}.\)​

(2) 乘法符合左分配率和右分配率: \(\bm A(\bm B+\bm C)=\bm A\bm B+\bm A\bm C\), \((\bm B+\bm C)\bm A=\bm B\bm A+\bm C\bm A\).

(3) 对单位矩阵 \(\bm I_n\), 有 \(\bm I\bm A=\bm A\bm I=\bm A\).

(4) 数乘与乘法的结合律: \(k(\bm A\bm B)=(k\bm A)\bm B=\bm A(k\bm B)\).

称 \(k\bm I\) 为数量矩阵, 易得它对加法, 数乘, 乘法运算封闭.

若 \(\bm A\bm B=\bm B\bm A\), 则称 \(\bm A\) 和 \(\bm B\) 可交换. 易得数量矩阵和任一同阶矩阵可交换.

幂运算: \(\bm A^m \overset{\mathrm{def}}{=}\bm A\bull\cdots\bull\bm A\), \(\bm A^0 \overset{\mathrm{def}}{=}\bm I\).

若 \(\bm A\) 和 \(\bm B\) 可交换, 则有二项式定理: \(\displaystyle (\bm A+\bm B)^m=\sum_{k=0}^m {m\choose k}\bm A^k\bm B^{m-k}\).

转置: 若 \(\bm A=(a_{ij})\), \(\bm A'=(a_{ji})\).

(1) \((\bm A+\bm B)'=\bm A'+\bm B'\); (2) \((k\bm A)'=k\bm A\); (3) \((\bm A\bm B)'=\bm B'\bm A'\).

对 (3), \(\displaystyle [(\bm A\bm B)']_{(j,i)}=[\bm A\bm B]_{(i,j)}=\sum_{k=1}^n a_{ik}b_{kj}=\sum_{k=1}^n [\bm B']_{(j,k)}[\bm A']_{(k,i)}=[\bm B'\bm A']_{(j,i)}\).

用矩阵可以简洁地表示线性方程组: \(\bm A\bm x=\bm\beta\).

矩阵乘法的另一表述方式: 若 \(\bm A\) 的列向量组为 \(\bm\alpha_1,\cdots,\bm\alpha_n\), 可记 \(\bm A=(\bm\alpha_1,\cdots,\bm\alpha_n)\), 则

\[\begin{aligned} \bm A\bm B&=(\bm\alpha_1,\cdots,\bm\alpha_n) \begin{pmatrix}b_{11}&b_{12}&\cdots&b_{1m}\\b_{21}&b_{22}&\cdots&b_{2m}\\\vdots&\vdots&&\vdots\\b_{n1}&b_{n2}&\cdots&b_{nm}\end{pmatrix}\\ &=(b_{11}\bm\alpha_1+b_{21}\bm\alpha_2+\cdots+b_{n1}\bm\alpha_n,\cdots,b_{1m}\bm\alpha_1+b_{2m}\bm\alpha_2+\cdots+b_{nm}\bm\alpha_n) \end{aligned} \]

类似地, 设 \(\bm{B}=(b_{ij})_{n\times m}\)的行向量组为 \(\bm{\gamma}_1,\cdots,\bm{\gamma}_n\), 则

\[\bm{AB}=\begin{pmatrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\ \vdots&\vdots&&\vdots\\a_{s1}&a_{s2}&\cdots&a_{sn}\end{pmatrix}\begin{pmatrix}\bm{\gamma}_1\\ \bm{\gamma}_2\\ \vdots\\ \bm{\gamma}_n\end{pmatrix}=\begin{pmatrix}a_{11}\bm{\gamma}_1+a_{12}\bm{\gamma}_2+\cdots+a_{1n}\bm{\gamma}_n\\a_{21}\bm{\gamma}_1+a_{22}\bm{\gamma}_2+\cdots+a_{2n}\bm{\gamma}_n\\ \vdots\\a_{s1}\bm{\gamma}_1+a_{s2}\bm{\gamma}_2+\cdots+a_{sn}\bm{\gamma}_n\end{pmatrix} \]

例 4.1.4:设 \(\bm A,\bm B\) 都是 \(n\) 阶方阵, 定义换位子: \([\bm A,\bm B]\xlongequal[]{\mathrm{def}}\bm A\bm B-\bm B\bm A\). 证明:

(1) \([k_1\bm A+k_2\bm B,\bm C]=k_1[\bm A,\bm C]+k_2[\bm B,\bm C]\),

(2) \([\bm A,\bm B]=-[\bm B,\bm A]\),

(3) \([\bm A,[\bm B,\bm C]]+[\bm B,[\bm C,\bm A]]+[\bm C,[\bm A,\bm B]]=0\).

例 4.1.6: 设 \(\bm A=\begin{pmatrix} 2&3\\ 0&2\end{pmatrix}\), 求 \(\bm A^m\).

\(\bm A=\begin{pmatrix} 2&0\\ 0&2\end{pmatrix}+\begin{pmatrix} 0&3\\ 0&0\end{pmatrix}=2\bm I+3\bm B\), 而 \(\bm B^2=\bm0\), \(\bm I\) 与 \(\bm B\) 可交换, 利用二项式定理:

\[\begin{aligned}\bm A^m&=(2\bm I+3\bm B)^m=(2\bm I)^m+m(2\bm I)^{m-1}(3\bm B)\\ &=2^m\bm I+3m2^{m-1}\bm B\\ &=\begin{pmatrix}2^m & 3m\cdot 2^{m-1}\\ 0 &2^m \end{pmatrix} \end{aligned} \]

例 4.1.7: 设 \(\bm A=\begin{pmatrix} a&c\\ 0&b\end{pmatrix}\), 求 \(\bm A^m\).

\(\bm A^2=\begin{pmatrix}a^2 &(a+b)c\\ 0&b^2 \end{pmatrix}\), \(\bm A^3=\begin{pmatrix} a^3&(a^2+ab+b^2)c\\ 0&b\end{pmatrix}\),

设 \(\bm A^{m-1}=\begin{pmatrix} a^{m-1}&(a^{m-2}+a^{m-3}b+\cdots+b^{m-2}) c \\ 0&b^{m-1}\end{pmatrix}\), 则 \(\bm A^{m}=\begin{pmatrix} a^{m}&(a^{m-1}+a^{m-2}b+\cdots+b^{m-1}) c \\ 0&b^{m}\end{pmatrix}\).

例 4.1.8: 设 \(\bm A=\begin{pmatrix}\cos\varphi &-\sin\varphi\\ \sin\varphi &\cos\varphi \end{pmatrix}\), 求 \(\bm A^m\).

设 \(\bm A^{m-1}=\begin{pmatrix}\cos(m-1)\varphi &-\sin(m-1)\varphi\\ \sin(m-1)\varphi &\cos(m-1)\varphi \end{pmatrix}\), 则 \(\bm A^m=\begin{pmatrix}\cos m\varphi &-\sin m\varphi\\ \sin m\varphi &\cos m\varphi \end{pmatrix}\).

\(\bm A \bm x\) 表示把向量 \(\bm x\) 逆时针旋转 \(\varphi\) 后的新向量.

例 4.1.9: 设 \(\bm A=\begin{pmatrix}0&1&0&\cdots&0\\0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&&\vdots\\0&0&0&\cdots&1\\0&0&0&\cdots&0\end{pmatrix}_{n\times n}=\begin{pmatrix}\bm0_{(n-1)\times1} &\bm I_{(n-1)\times(n-1)}\\ 0& \bm0_{1\times(n-1)} \end{pmatrix}\), 求 \(\bm A^m\).

\(\bm A^2=\begin{pmatrix}0&0&1&0&\cdots&0\\0&0&0&1&\cdots&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots\\0&0&0&0&\cdots&1\\0&0&0&0&\cdots&0\\0&0&0&0&\cdots&0\end{pmatrix}\), 设 \(\bm A^{m-1}=\begin{pmatrix}\bm0_{(n-1)\times(m-1)} &\bm I_{(n-m+1)\times(n-m+1)}\\ \bm0& \bm0_{(m-1)\times(n-1)} \end{pmatrix}\),

则 \(\bm A^m=\begin{pmatrix}\bm0_{(n-1)\times m} &\bm I_{(n-m)\times(n-m)}\\ \bm0& \bm0_{m\times(n-1)} \end{pmatrix}\), 当 \(m\geq n\) 时, \(\bm A^m=\bm0\). 注意到 \(\mathrm{rank}(\bm A^m)=\max\{n-m,0\}\).

例 4.1.10: 设 \(\bm A\) 是 \(K\) 上的 \(s\times n\) 矩阵, 若对任意列向量 \(\bm\eta\in K^n\), 有 \(\bm A\bm\eta=\bm0\), 则 \(\bm A=\bm0\).

依题意得 \(n\) 元齐次方程组 \(\bm A\bm x=\bm0\) 的解空间 \(W=K^n\), 故 \(\mathrm{rank}(\bm A)=n-\dim W=0\), 故 \(\bm A=\bm0\).

例 4.1.11: 设 \(\bm A=\begin{pmatrix}3&1&0\\ 0&3&1\\ 0&0&3 \end{pmatrix}\), 求与 \(\bm A\) 可交换的所有矩阵.

\(\bm A=\begin{pmatrix}3&0&0\\ 0&3&0\\ 0&0&3 \end{pmatrix}+\begin{pmatrix}0&1&0\\ 0&0&1\\ 0&0&0 \end{pmatrix}=3\bm I+\bm B\), 设 \(\bm X=(x_{ij})\)​, 则 \(\bm A\) 与 \(\bm X\) 可交换 \(\Longleftrightarrow\) \(\bm B\) 与 \(\bm X\) 可交换.

\[\bm B\bm X=\begin{pmatrix}x_{21}&x_{22}&x_{23}\\ x_{31}&x_{32}&x_{33}\\ 0&0&0 \end{pmatrix} =\begin{pmatrix}0&x_{11}&x_{12}\\ 0&x_{21}&x_{22}\\ 0&x_{31}&x_{32} \end{pmatrix}=\bm X\bm B \]

于是 \(x_{21}=x_{31}=x_{32}=0\), \(x_{11}=x_{22}=x_{33}=a\), \(x_{23}=x_{12}=b\), 即 \(\bm X=\begin{pmatrix}a&b&x_{13}\\ 0&a&b\\ 0&0&a \end{pmatrix}\).

习题 4.1.7: 设 \(\bm A=\begin{pmatrix}\lambda&1&0&0&\cdots&0&0\\0&\lambda&1&0&\cdots&0&0\\ \vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\0&0&0&0&\cdots&\lambda&1\\0&0&0&0&\cdots&0&\lambda\end{pmatrix}_{n\times n}\), 求 \(\bm A^m\).

利用例 4.1.9, \(\bm A=\lambda \bm I+\bm B\), \(\bm B^k=\begin{pmatrix}\bm0 &\bm I_{(n-k)\times(n-k)}\\ \bm0& \bm0\end{pmatrix}\), 故

\[\begin{aligned} \bm A^m&=\lambda^m\bm I+C_m^1\lambda^{m-1}\bm B+\cdots+C_m^{m-1}\lambda\bm B^{m-1}+\bm B^m\\&=\begin{pmatrix} &\lambda^m&m\lambda^{m-1}&\cdots&\mathbb{C}_m^{m-1}\lambda&1&0&0&\cdots&0\\ &&\lambda^m&m\lambda^{m-1}&\cdots&\mathbb{C}_m^{m-1}\lambda&1&0&\cdots&0\\ &&&&\ddots&\ddots&\ddots&\ddots&\ddots&\vdots\\ &&&&&\ddots&\ddots&\ddots&\ddots&0\\ &&&&&&&&&1\\ &&&&&\lambda^m&m\lambda^{m-1}&\cdots&\cdots&\mathbb{C}_m^{m-1}\lambda\\ &&&&&&\ddots&\ddots&&\vdots\\&&&&&&&&\lambda^m&m\lambda^{m-1}\\ &&&&&&&&&\lambda^m\end{pmatrix} \end{aligned} \]

习题 4.1.8: 计算 \(\bm A^m=\begin{pmatrix}2&-1\\ 3&-2 \end{pmatrix}^m\).

\(\bm A^2=\bm I\), 故 \(m\) 为奇数时, \(\bm A^m=\bm A\), \(m\) 为偶数时, \(\bm A^m=\bm I\).

特殊矩阵

定义 4.2.1: 除了主对角线, 其余元素都为 0 的矩阵称为对角矩阵.

命题 4.2.1: 用对角矩阵 \(\mathrm{diag}(d_1,\cdots,d_n)\) 左乘(右乘)矩阵 \(\bm A\), 相当于用主对角元分别乘 \(\bm A\) 对应的行(列).

\[\mathrm{diag}(d_1,\cdots,d_n)\begin{pmatrix} \bm\gamma_1\\ \bm\gamma_2\\ \vdots\\ \bm\gamma_n \end{pmatrix}=\begin{pmatrix} d_1\bm\gamma_1\\ d_2\bm\gamma_2\\ \vdots\\ d_n\bm\gamma_n \end{pmatrix}\\ (\bm\alpha_1,\cdots,\bm\alpha_n)\cdot\mathrm{diag}(d_1,\cdots,d_n)=(d_1\bm\alpha_1,\cdots,d_n\bm\alpha_n) \]

定义 4.2.2: 只有 \((i,j)\) 元为 1, 其余元素为 0 的矩阵称为基本矩阵, 记住 \(\bm E_{ij}\).

设 \(\bm A=(a_{ij})\), 则 \(\displaystyle \bm A=\sum_{i=1}^n\sum_{j=1}^m a_{ij}\bm E_{ij}\).

命题 4.2.2: 用 \(\bm E_{ij}\) 左乘 \(\bm A\), 相当于把 \(\bm A\) 的第 \(j\) 行移到第 \(i\) 行, 其余行皆为 0. 用 \(\bm E_{ij}\) 右乘 \(\bm A\), 相当于把 \(\bm A\) 的第 \(i\) 列移到第 \(j\) 列, 其余列皆为 0

​​

由命题 4.2.2 可得到:

\[(1)\:\bm E_{ij}\bm E_{kl}=\begin{cases}\bm E_{il} &k=j\\ \bm0 &k\neq j \end{cases},\quad (2)\:\bm E_{ij}\bm A\bm E_{kl}=a_{jk}\bm E_{il} \]

定义 4.2.3: 主对角线下方(上方)元素全为 0 的方阵称为上(下)三角矩阵.

上三角矩阵满足 \(a_{ij}=0,\:(i>j)\)​, 且 \(\bm A=\displaystyle \sum_{i=1}^n \sum_{j=i}^n a_{ij}\bm E_{ij}\).

命题 4.2.3: \(n\) 阶上三角矩阵 \(\bm A,\bm B\) 的乘积仍是上三角矩阵, 且 \(\bm A\bm B\) 的主对角元等于 \(\bm A\) 和 \(\bm B\) 相应主对角元的乘积.

(1) \(\displaystyle [\bm A\bm B]_{(i,j)}=\sum_{k=1}^n a_{ik}b_{kj}=\sum_{k=1}^j a_{ik}b_{kj}+\sum_{k=j+1}^n a_{ik}b_{kj}\), 而 \(k>j\) 时, \(b_{kj}=0\),

于是 \(\displaystyle [\bm A\bm B]_{(i,j)}=\sum_{k=1}^j a_{ik}b_{kj}\), 当 \(i>j\) 时, \(a_{ik}=0\), 故 \([\bm A\bm B]_{(i,j)}=0,\:(i>j)\), \(\bm A\bm B\) 是上三角矩阵.

\(\displaystyle [\bm A\bm B]_{(i,i)}=\sum_{k=1}^i a_{ik}b_{ki}=a_{ii}b_{ii}\).

(2)

\[\begin{aligned} \bm A\bm B&=\left(\sum_{i=1}^n \sum_{j=i}^n a_{ij}\bm E_{ij}\right)\left(\sum_{k=1}^n\sum_{l=k}^n b_{kl}\bm E_{kl}\right)\\ &=\sum_{i=1}^n \sum_{j=i}^n\sum_{k=1}^n\sum_{l=k}^n a_{ij}b_{kl}\bm E_{ij}\bm E_{kl}\\ &=\sum_{i=1}^n \sum_{j=i}^n \sum_{l=j}^n a_{ij}b_{jl}\bm E_{ij}\bm E_{jl}\\ &=\sum_{i=1}^n \sum_{l=i}^n \left(\sum_{j=i}^l a_{ij}b_{jl}\right)\bm E_{il} \end{aligned} \]

定义 4.2.4:单位矩阵经过一次初等行(列)变换得到的矩阵称为初等矩阵.

(1) \(\bm P(j,i(k))\): \(\textcircled{j}+k\textcircled{i}\).

(2) \(\bm P(i,j)\): \(\textcircled{j}\) 与 \(\textcircled{i}\) 互换.

(3) \(\bm P(i(c))\): \(c\cdot\textcircled{i}\).

定理 4.2.1: 用初等矩阵左乘(右乘) \(\bm A\), 相当于对 \(\bm A\) 作一次相应的初等行(列)变换.

将初等变换转化为矩阵乘法, 以便于使用矩阵乘法的运算性质.

定义 4.2.5: 若 \(\bm A'=\bm A\), 则称 \(\bm A\) 是对称矩阵.

若 \(\bm A,\bm B\) 是对称矩阵, 则 \(k\bm A\) 和 \(\bm A+\bm B\) 也是对称矩阵.

命题 4.2.5: 设 \(\bm A,\bm B\) 是 \(n\) 阶对称矩阵, 则 \(\bm A\bm B\) 对称的充要条件是 \(\bm A\) 与 \(\bm B\) 可交换.

\(\bm A\bm B\) 对称 \(\Longleftrightarrow\) \((\bm A\bm B)'=\bm A\bm B\) \(\Longleftrightarrow\) \(\bm B\bm A=\bm A\bm B\).

定义 4.2.6: 若 \(\bm A'=-\bm A\), 则称 \(\bm A\) 是斜对称矩阵.

可以看出, \(\bm A(i,i)=0\), \(\bm A(i,j)=-\bm A(j,i)\).

若 \(\bm A,\bm B\) 是斜对称矩阵, 则 \(k\bm A\) 和 \(\bm A+\bm B\) 也是斜对称矩阵.

命题 4.2.6: 奇数阶斜对称矩阵的行列式为 0.

\(|\bm A|=|\bm A'|=|-\bm A|=(-1)^{n}|\bm A|\).

例 4.2.1: 证明: 若 \(\bm D\) 是主对角线元两两不等的对角矩阵, 则与 \(\bm D\) 可交换的矩阵一定是对角矩阵.

设 \(\bm D=\mathrm{diag}(d_1,\cdots,d_n)\), \(\bm A=(a_{ij})\), 则 \((\bm D\bm A)_{(i,j)}=d_ia_{ij}\), \((\bm A\bm D)_{(i,j)}=a_{ij}d_j.\)

因 \((\bm D\bm A)=(\bm A\bm D)\), 且 \(i\neq j\) 时 \(d_i\neq d_j\), 故 \(a_{ij}=0\), \((i\neq j)\), 即 \(\bm A\) 是对角矩阵.

例 4.2.2: 证明: 与所有 \(n\) 阶矩阵可交换的矩阵一定是 \(n\) 阶数量矩阵.

设 \(\bm A=(a_{ij})\) 与所有 \(n\) 阶矩阵可交换, 则 \(\bm A\) 与基本矩阵 \(\bm E_{1j}\) 可交换, 即 \(\bm E_{1j}\bm A=\bm A\bm E_{1j}\):

\[\begin{pmatrix}a_{j1}&a_{j2}&\cdots&a_{jj}&\cdots&a_{jn}\\0&0&\cdots&0&\cdots&0\\ \vdots&\vdots&&\vdots&&\vdots\\0&0&\cdots&0&\cdots&0\end{pmatrix}=\begin{pmatrix}0&\cdots&0&a_{11}&0&\cdots&0\\0&\cdots&0&a_{21}&0&\cdots&0\\ \vdots&&\vdots&\vdots&\vdots&&\vdots\\0&\cdots&0&a_{n1}&0&\cdots&0\end{pmatrix} \]

故 \(a_{jj}=a_{11}\), 其余为 0. 令 \(j=1,\cdots,n\), 得 \(a_{11}=\cdots=a_{nn}\), 故 \(\bm A\) 是数量矩阵.

例 4.2.3: 任一 \(n\) 阶矩阵 \(\bm A\) 都可表示为一个对称矩阵和一个斜对称矩阵之和, 且表示法唯一.

\[\bm A=\frac12(\bm A+\bm A')+\frac12(\bm A-\bm A') \]

其中 \(\dfrac12(\bm A+\bm A')\) 是对称矩阵, \(\dfrac12(\bm A-\bm A')\) 是斜对称矩阵.

设还有一种表示法 \(\bm A=\bm A_1+\bm A_2\), 则 \(\bm A'=\bm A_1-\bm A_2\),

联立解得 \(\bm A_1=\dfrac12(\bm A+\bm A')\), \(\bm A_2=\dfrac12(\bm A-\bm A')\), 故表示法唯一.

例 4.2.5: 设 \(\bm A\) 是实对称矩阵, 证明: 若 \(\bm A^2=\bm0\), 则 \(\bm A=\bm0\).

\(\displaystyle (\bm A^2)_{(i,i)}=\sum_{k=1}^n a_{ik}a_{ki}=\sum_{k=1}^n a_{ik}^2=0\), 故 \(\forall i,k\in\{1,\cdots,n\}\), \(a_{ik}=0\), 因此 \(\bm A=\bm0\).

例 4.2.6: 设 \(\bm A_{s\times n}\) 的秩为 \(r\), 证明: 若 \(\bm A\) 的行向量组和列向量组的极大无关组分别为 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r}\) 和 \(\bm\alpha_{j_1},\cdots,\bm\alpha_{j_r}\), 则 \(r\) 阶子式 \(\bm A\begin{pmatrix}i_1,i_2,\cdots,i_r\\ j_1,j_2,\cdots,j_r\end{pmatrix}\neq0\).

令 \(\bm A_1=(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r})\), 则 \(\bm A_1\) 的行向量组 \(\widetilde{\bm\gamma}_1,\cdots,\widetilde{\bm\gamma}_s\)是 \(\bm A\) 的行向量组 \(\bm\gamma_1,\cdots,\bm\gamma_s\) 的缩短组. 于是每个 \(\widetilde{\bm\gamma}_i\) 都可被 \(\widetilde{\bm\gamma}_{i_1},\cdots,\widetilde{\bm\gamma}_{i_r}\) 线性表出,

而 \(\mathrm{rank}(\bm A_1)=r\), 由例 3.3.3得 \(\widetilde{\bm\gamma}_{i_1},\cdots,\widetilde{\bm\gamma}_{i_r}\) 是 \(\bm A_1\) 行向量组的极大无关组, 故 \(\bm A\begin{pmatrix}i_1,i_2,\cdots,i_r\\ j_1,j_2,\cdots,j_r\end{pmatrix}\neq0\).

例 4.2.7: 证明: 斜对称矩阵的秩为偶数.

设斜对称矩阵 \(\bm A\) 的行向量组为 \(\bm\gamma_1,\cdots,\bm\gamma_n\), 则列向量组为 \(-\bm\gamma_1',\cdots,-\bm\gamma_n'\).

设 \(\mathrm{rank}(\bm A)=r\), 取行向量组的极大无关组 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r}\), 则 \(-\bm\gamma_{i_1}',\cdots,-\bm\gamma_{i_r}'\)是列向量组的极大无关组.

由例 4.2.6 得 \(\bm A\begin{pmatrix}i_1,i_2,\cdots,i_r\\ i_1,i_2,\cdots,i_r\end{pmatrix}\neq0\), 而这个子式也是斜对称矩阵的行列式, 又因奇数阶斜对称矩阵的行列式为 0, 故 \(r\) 一定是偶数.

例 4.2.9: 若存在 \(k\in\Z^+\) 使得 \(\bm A^k=\bm0\), 则称 \(\bm A\) 为幂零矩阵, 满足条件的最小 \(k\) 称为幂零指数. 证明:

(1) 上三角矩阵是幂零矩阵的充要条件是主对角元全为 0.

(2) 若 \(n\) 阶上三角矩阵是幂零矩阵, 则幂零指数 \(k\leq n\).

\((\Rightarrow)\) 若上三角矩阵 \(\bm A\) 是幂零矩阵, 假设某个主对角元 \((i,i)\) 不为零, 则 \((\bm A^m)_{(i,i)}=a_{ii}^m\neq0\), 矛盾.

\((\Leftarrow)\) 若 \(\bm A\) 主对角元全为 0, 显然 \(\bm A^k\) 主对角元全为 0. 由命题 4.2.3 证明 (2)得:

\[(\bm A^2)_{(i,i+1)}=a_{ii}a_{i,i+1}+a_{i,i+1}a_{i+1,i+1}=0,\quad i=1,\cdots,n-1 \]

假设 \((\bm A^k)_{(i,i+1)}=\cdots=(\bm A^k)_{(i,i+k-1)}=0\), 则对 \(m:1\leq m\leq k\), 有

\[\begin{aligned} (\bm A^{k+1})_{(i,i+m)}&=\sum_{j=i}^{i+m}(\bm A^k)_{(i,j)} a_{j,i+m}\\ &=(\bm A^k)_{i,i}a_{i,i+m}+\cdots+(\bm A^k)_{(i,i+m)}a_{i+m,i+m}=0 \end{aligned} \]

归纳得, \(\forall k\geq2\), 有 \((\bm A^k)_{(i,i+1)}=\cdots=(\bm A^k)_{(i,i+k-1)}=0\), 故 \(\bm A^n=\bm0\), \(\bm A\) 是幂零矩阵.

同时可以看出, 幂零指数 \(k\leq n\).

例 4.2.10: \(n\) 阶循环位移矩阵如下:

\[\bm C=\begin{pmatrix}0&1&0&\cdots&0&0\\0&0&1&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\0&0&0&\cdots&0&1\\1&0&0&\cdots&0&0\end{pmatrix} \]

(1) 用 \(\bm C\) 左乘 \(\bm A\), 相当于把 \(\bm A\) 的行上移一行, 第一行换到最后一行; 用 \(\bm C\) 右乘 \(\bm A\), 相当于把 \(\bm A\) 的列右移一列, 最后一列换到第一列.

(2) \(\displaystyle \sum_{k=0}^{n-1}\bm C^k=\bm J\), 其中 \(\bm J\) 的元素全为 1.

\[\begin{pmatrix}0&1&0&\cdots&0&0\\0&0&1&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\0&0&0&\cdots&0&1\\1&0&0&\cdots&0&0\end{pmatrix} \begin{pmatrix} \bm{\delta}_1\\ \bm{\delta}_2\\ \vdots\\ \bm{\delta}_n \end{pmatrix} =\begin{pmatrix}\bm{\delta}_2\\ \bm{\delta}_3\\ \vdots\\ \bm{\delta}_n\\ \bm{\delta}_1\end{pmatrix} \]

\[(\bm{\alpha}_{1},\bm{\alpha}_{2},\cdots,\bm{\alpha}_{n}) \begin{pmatrix}0&1&0&\cdots&0&0\\0&0&1&\cdots&0&0\\ \vdots&\vdots&\vdots&&\vdots&\vdots\\0&0&0&\cdots&0&1\\1&0&0&\cdots&0&0\end{pmatrix} =(\bm{\alpha}_{n} ,\bm{\alpha}_{1} ,\bm{\alpha}_{2} ,\cdots,\bm{\alpha}_{n-1} ) \]

显然 \(\bm C=\bm I\), \(\bm C=(\bm\varepsilon_n,\bm\varepsilon_1,\cdots,\bm\varepsilon_{n-1})\), 利用 (1) 的结论得:

\(\bm C^2=(\bm\varepsilon_{n-1},\bm\varepsilon_n,\bm\varepsilon_1,\cdots,\bm\varepsilon_{n-2}),\bm C^3=(\bm\varepsilon_{n-2},\bm\varepsilon_{n-1},\bm\varepsilon_n,\cdots,\bm\varepsilon_{n-3}),\cdots ,\bm C^{n-1}=(\bm\varepsilon_2,\cdots,\bm\varepsilon_n,\bm\varepsilon_1)\),

于是 \(\displaystyle \sum_{k=0}^{n-1}\bm C^k=\bm J\).

例 4.2.11: 循环矩阵如下:

\[\bm{A}=\begin{pmatrix}a_1&a_2&a_3&\cdots&a_n\\a_n&a_1&a_2&\cdots&a_{n-1}\\ \vdots&\vdots&\vdots&&\vdots\\a_2&a_3&a_4&\cdots&a_1\end{pmatrix} \]

证明: \(\bm A=a_1\bm I+a_2\bm C+\cdots+a_n\bm C^{n-1}\).

\[\begin{aligned} &a_1\bm I+a_2\bm C+\cdots+a_n\bm C^{n-1}\\ =&(a_1\bm\varepsilon_1+a_2\bm\varepsilon_n+\cdots+a_n\bm\varepsilon_1,\cdots,a_1\bm\varepsilon_n+a_2\bm\varepsilon_{n-1}+\cdots+a_n\bm\varepsilon_1)\\ =&\bm A \end{aligned} \]

习题 4.2.9: 设 \(\bm A,\bm B\) 是对称矩阵, 则 \(\forall m\in\Z^+\), \(\bm C=(\bm A\bm B)^m\bm A\) 也是对称矩阵.

\(\bm C'=\bm A'(\bm B'\bm A')^m=\bm A\cdot(\bm B\bm A)\cdots(\bm B\bm A)=(\bm A\bm B)^m\bm A\).

习题 4.2.12: 证明两个 \(n\) 阶循环矩阵的乘积仍是循环矩阵.

\[\begin{aligned} \bm A\bm B&=(a_1\bm I+a_2\bm C+\cdots+a_n\bm C^{n-1})(b_1\bm I+b_2\bm C+\cdots+b_n\bm C^{n-1})\\ &=a_1b_1\bm I+(a_1b_2+a_2b_1)\bm C+\cdots+a_nb_n\bm C^{2n-2}\\ &=\sum_{k=0}^{2n-2} \sum_{j=1}^{k+2} a_jb_{k+2-j}\bm C^k \end{aligned} \]

注意到 \(\bm C^n=\bm I\), 故

\[\begin{aligned} \bm A\bm B&=\sum_{k=0}^{n-1} \sum_{j=1}^{k+2} a_jb_{k+2-j}\bm C^k+\sum_{k=n}^{2n-2} \sum_{j=1}^{k+2} a_jb_{k+2-j}\bm C^k\\ &=\sum_{k=0}^{n-1} \sum_{j=1}^{k+2} a_jb_{k+2-j}\bm C^k+\sum_{l=0}^{n-2} \sum_{j=1}^{l+n+2} a_jb_{l+n+2-j}\bm C^{l+n}\\ &=\sum_{k=0}^{n-1} c_k\bm C^k \end{aligned} \]

习题 4.2.13: 设 \(\bm A\) 是实数域上的上三角矩阵, 证明: 若 \(\bm A\) 和 \(\bm A'\) 可交换, 则 \(\bm A\) 是对角矩阵.

\(\displaystyle (\bm A\bm A')_{(i,i)}=\sum_{k=1}^n a_{ik}^2=\displaystyle (\bm A'\bm A)_{(i,i)}=\sum_{k=1}^n a_{ki}^2\),

因 \(\bm A\) 是上三角矩阵, 故当 \(k<i\) 时, \(a_{ik}=0\), 当 \(k>i\) 时, \(a_{ki}=0\), 于是 \(\displaystyle \sum_{k=i}^n a_{ik}^2=\sum_{k=1}^i a_{ki}^2\).

令 \(i=1\), 得 \(a_{11}^2+a_{12}^2+\cdots+a_{1n}^2=a_{11}^2\), 故 \(a_{12}=\cdots=a_{1n}=0\);

令 \(i=2\), 得 \(a_{22}^2+a_{23}^2+\cdots+a_{2n}^2=a_{12}^2+a_{22}^2\), 故 \(a_{22}=\cdots=a_{2n}=0\);

以此类推, 得 \(a_{11},\cdots,a_{nn}\) 可以取任何值, 而其余元素只能为 0, 即 \(\bm A\) 是对角矩阵.

矩阵乘积的秩和行列式

定理 4.3.1: \(\mathrm{rank}(\bm A\bm B)\leq \min\{\mathrm{rank}(\bm A),\mathrm{rank}(\bm B)\}\).

设 \(\bm A_{s\times n}\), \(\bm B_{n\times m}\), 设 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 是 \(\bm A\) 的列向量组, 则

\[\begin{aligned} \bm A\bm B&= (\bm{\alpha}_1,\bm{\alpha}_2,\cdots,\bm{\alpha}_n)\begin{pmatrix}b_{11}&b_{12}&\cdots&b_{1m}\\b_{21}&b_{22}&\cdots&b_{2m}\\ \vdots&\vdots&&\vdots\\b_{n1}&b_{n2}&\cdots&b_{nm}\end{pmatrix}\\ &=(b_{11}\bm{\alpha}_{1}+b_{21}\bm{\alpha}_{2}+\cdots+b_{n1}\bm{\alpha}_{n},\cdots,b_{1m}\bm{\alpha}_{1}+b_{2m}\bm{\alpha}_{2}+\cdots+b_{nm}\bm{\alpha}_{n}) \end{aligned} \]

故 \(\bm A\bm B\) 的列向量组可以被 \(\bm\alpha_1,\cdots,\bm\alpha_n\) 线性表出, 于是 \(\mathrm{rank}(\bm A\bm B)\leq \mathrm{rank}(\bm A)\).

同理 \(\bm A\bm B\) 的行向量组可被 \(\bm B\) 的行向量组线性表出, 于是 \(\mathrm{rank}(\bm A\bm B)\leq \mathrm{rank}(\bm B)\).

定理 4.3.2: 设 \(\bm A,\bm B\) 是 \(n\) 阶方阵, 则 \(|\bm A\bm B|=|\bm A||\bm B|\).

由推论 2.6.1得, \(\begin{vmatrix} \bm A &\bm0\\ -\bm I &\bm B \end{vmatrix}= \begin{vmatrix} a_{11}&a_{12}&\cdots&a_{1n}&0&0&\cdots&0\\ a_{21}&a_{22}&\cdots&a_{2n}&0&0&\cdots&0\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&0&0&\cdots&0\\ -1&0&\cdots&0&b_{11}&b_{12}&\cdots&b_{1n}\\ 0&-1&\cdots&0&b_{21}&b_{22}&\cdots&b_{2n}\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\ 0&0&\cdots&-1&b_{n1}&b_{n2}&\cdots&b_{nn} \end{vmatrix} =|\bm A||\bm B|\).

对 \(k=n+1,\cdots,2n\), 将第 \(k\) 行乘以 \(a_{1k}\) 并加到第一行, 得:

\[\begin{vmatrix} 0&0&\cdots&0&\displaystyle \sum_{k=1}^na_{1k}b_{k1}&\displaystyle \sum_{k=1}^na_{1k}b_{k2}&\cdots&\displaystyle \sum_{k=1}^na_{1k}b_{kn}\\ a_{21}&a_{22}&\cdots&a_{2n}&0&0&\cdots&0\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&0&0&\cdots&0\\ -1&0&\cdots&0&b_{11}&b_{12}&\cdots&b_{1n}\\ 0&-1&\cdots&0&b_{21}&b_{22}&\cdots&b_{2n}\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\ 0&0&\cdots&-1&b_{n1}&b_{n2}&\cdots&b_{nn} \end{vmatrix} \]

类似地, 将第 \(k\) 行乘以 \(a_{ik}\) 并加到第 \(i\) 行, 得:

\[\begin{vmatrix} 0&0&\cdots&0&\sum_{k=1}^na_{1k}b_{k1}&\sum_{k=1}^na_{1k}b_{k2}&\cdots&\sum_{k=1}^na_{1k}b_{kn}\\[2pt] 0&0&\cdots&0&\sum_{k=1}^na_{2k}b_{k1}&\sum_{k=1}^na_{2k}b_{k2}&\cdots&\sum_{k=1}^na_{2k}b_{kn}\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\ 0&0&\cdots&0&\sum_{k=1}^na_{nk}b_{k1}&\sum_{k=1}^na_{nk}b_{k2}&\cdots&\sum_{k=1}^na_{nk}b_{kn}\\ -1&0&\cdots&0&b_{11}&b_{12}&\cdots&b_{1n}\\0&-1&\cdots&0&b_{21}&b_{22}&\cdots&b_{2n}\\ \vdots&\vdots&&\vdots&\vdots&\vdots&&\vdots\\0&0&\cdots&-1&b_{n1}&b_{n2}&\cdots&b_{nn} \end{vmatrix} =\begin{vmatrix} \bm0 &\bm A\bm B\\ -\bm I &\bm B \end{vmatrix} \]

由Laplace 定理得,

\[\begin{vmatrix} \bm0 &\bm A\bm B\\ -\bm I &\bm B \end{vmatrix}= |\bm A\bm B|(-1)^{(1+\cdots+n)+[(n+1)+\cdots+2n]}|-\bm I|=|\bm A\bm B| \]

利用归纳法, 可以推广到多个 \(n\) 阶矩阵相乘的情形:

\[|\bm A_1\bm A_2\cdots \bm A_m|=|\bm A_1||\bm A_2|\cdots|\bm A_m| \]

定理 4.3.3 (Binet-Cauchy) : 设 \(\bm A_{s\times n}\), \(\bm B_{n\times s}\),

(1) 若 \(s>n\), 则 \(|\bm A\bm B|=0\);

(2) 若 \(s\leq n\), 则 \(|\bm A\bm B|\) 等于 \(\bm A\) 的所有 \(s\) 阶子式与 \(\bm B\) 的对应 \(s\) 阶子式的乘积之和,

\[|\bm A\bm B|=\sum_{1\leq j_1<\cdots<j_s\leq n}\bm A \begin{pmatrix}1,2,\cdots,s\\ j_1,j_2,\cdots,j_s \end{pmatrix} \bm B \begin{pmatrix}j_1,j_2,\cdots,j_s\\ 1,2,\cdots,s\end{pmatrix} \]

若 \(s>n\), 则 \(\mathrm{rank}(\bm A\bm B)\leq \min\{\mathrm{rank}(\bm A),\mathrm{rank}(\bm B)\}\leq n<s\), 故 \(\bm A\bm B\) 不满秩, 行列式为 0.

若 \(s\leq n\), 设 \(D=\begin{vmatrix} \bm A_{s\times n} &\bm0\\ -\bm I_{n\times n} &\bm B_{n\times s} \end{vmatrix}\), 一方面, 利用Laplace 定理按前 \(s\) 行展开得:

\[D=\sum_{1\leq j_1<\cdots<j_s\leq n} \bm A \begin{pmatrix}1,2,\cdots,s\\ j_1,j_2,\cdots,j_s \end{pmatrix} (-1)^{(1+\cdots+s)+(j_1+\cdots+j_s)} \Big|(-\bm\varepsilon_{k_1},\cdots,-\bm\varepsilon_{k_{n-s}},\bm B)\Big| \]

其中 \(\{k_1,\cdots,k_{n-s}\}=\{1,\cdots,n\}\backslash \{j_1,\cdots,j_s\}\), 且 \(k_1<\cdots<k_{n-s}\).

对 \(\Big|(-\bm\varepsilon_{k_1},\cdots,-\bm\varepsilon_{k_{n-s}},\bm B)\Big|\) 按前 \(n-s\) 列展开, 而前 \(n-s\) 列只有一个不为 0 的子式:

\[\begin{aligned} \Big|(-\bm\varepsilon_{k_1},\cdots,-\bm\varepsilon_{k_{n-s}},\bm B)\Big|&=|-\bm I_{n-s}|(-1)^{[1+\cdots+(n-s)]+(k_1+\cdots+k_{n-s})} \bm B\begin{pmatrix}j_1,j_2,\cdots,j_s \\1,2,\cdots,s \end{pmatrix}\\ &=(-1)^{(n-s)+[1+\cdots+(n-s)]+(k_1+\cdots+k_{n-s})} \bm B\begin{pmatrix}j_1,j_2,\cdots,j_s \\1,2,\cdots,s \end{pmatrix} \end{aligned} \]

因为 \((-1)^{(1+\cdots+s)+(j_1+\cdots+j_s)+(n-s)+[1+\cdots+(n-s)]+(k_1+\cdots+k_{n-s})}=(-1)^{\frac12 s(s+1)+(n-s)+\frac12(n-s)(n-s+1)+\frac12n(n+1)}=(-1)^{s^2+n^2-s(n+1)}\), 于是

\[D=\sum_{1\leq j_1<\cdots<j_s\leq n} \bm A \begin{pmatrix}1,2,\cdots,s\\ j_1,j_2,\cdots,j_s \end{pmatrix} (-1)^{s^2+n^2-s(n+1)} \bm B\begin{pmatrix}j_1,j_2,\cdots,j_s \\1,2,\cdots,s \end{pmatrix} \]

另一方面, 对 \(D=\begin{vmatrix} \bm A_{s\times n} &\bm0\\ -\bm I_{n\times n} &\bm B_{n\times s} \end{vmatrix}\) 用定理 4.3.2 中的证明方法,

把第 \(k\) 行乘以 \(a_{ik}\) 加到第 \(i\) 行 (\(s+1\leq k\leq n+s, 1\leq i\leq s\)), 得到

\[\begin{aligned} D&=\begin{vmatrix} \bm0 &\bm A\bm B\\ -\bm I &\bm B \end{vmatrix}=|\bm A\bm B|(-1)^{(1+\cdots+s)+[(n+1)+\cdots+(n+s)]}|-\bm I_{n\times n}|\\ &=(-1)^{s^2+s+sn+n}|\bm A\bm B| \end{aligned} \]

综合两个结果, 得

\[|\bm A\bm B|=\sum_{1\leq j_1<\cdots<j_s\leq n}\bm A \begin{pmatrix}1,2,\cdots,s\\ j_1,j_2,\cdots,j_s \end{pmatrix} \bm B \begin{pmatrix}j_1,j_2,\cdots,j_s\\ 1,2,\cdots,s\end{pmatrix} \]

命题 4.3.1:设 \(\bm A_{s\times n}\), \(\bm B_{n\times s}\), 且 \(r\leq s\),

(1) 若 \(r>n\), 则 \(\bm A\bm B\) 的任一 \(r\) 阶子式为 0;

(2) 若 \(r\leq n\), 则 \(\bm A\bm B\) 的任一 \(r\) 阶子式

\[\bm A\bm B \begin{pmatrix}i_1,i_2,\cdots,i_r\\ j_1,j_2,\cdots,j_r \end{pmatrix} =\sum_{1\leq k_1<\cdots<k_r\leq n}\bm A \begin{pmatrix}i_1,i_2,\cdots,i_r\\ k_1,k_2,\cdots,k_r \end{pmatrix} \bm B \begin{pmatrix}k_1,k_2,\cdots,k_r\\ j_1,j_2,\cdots,j_r \end{pmatrix} \]

\[\bm A\bm B \begin{pmatrix}i_1,i_2,\cdots,i_r\\ j_1,j_2,\cdots,j_r \end{pmatrix} =\left|\begin{pmatrix} a_{i_1,1}&a_{i_1,2}&\cdots&a_{i_1,n}\\ a_{i_2,1}&a_{i_2,2}&\cdots&a_{i_2,n}\\ \vdots&\vdots&&\vdots\\ a_{i_r,1}&a_{i_r,2}&\cdots&a_{i_r,n} \end{pmatrix} \begin{pmatrix}b_{1j_1}&b_{1j_2}&\cdots&b_{1j_r}\\ b_{2j_1}&b_{2j_2}&\cdots&b_{2j_r}\\ \vdots&\vdots&&\vdots\\ b_{nj_1}&b_{nj_2}&\cdots&b_{nj_r} \end{pmatrix}\right|=|\bm A_1\bm B_1| \]

若 \(r>n\), 则 \(\bm A_1\bm B_1\) 不满秩, 行列式为 0.

若 \(r\leq n\), 利用定理 4.3.3 (Binet-Cauchy)得:

\[\begin{aligned} |\bm A_1\bm B_1|& =\sum_{1\leq k_1<\cdots<k_r\leq n} \bm A_1\begin{pmatrix}1,2,\cdots,r\\ k_1,k_2,\cdots,k_r \end{pmatrix} \bm B_1\begin{pmatrix}k_1,k_2,\cdots,k_r\\ 1,2,\cdots,r \end{pmatrix}\\ &=\sum_{1\leq k_1<\cdots<k_r\leq n} \bm A\begin{pmatrix}i_1,i_2,\cdots,i_r\\ k_1,k_2,\cdots,k_r \end{pmatrix} \bm B\begin{pmatrix}k_1,k_2,\cdots,k_r\\ j_1,j_2,\cdots,j_r \end{pmatrix} \end{aligned} \]

如果 \(\bm A\) 一个子式的行列指标相同, 则称此子式为主子式.

例 4.3.1: 证明: \(\mathrm{rank}(\bm A+\bm B)\leq \mathrm{rank}(\bm A)+\mathrm{rank}(\bm B)\).

设 \(\bm A\) 和 \(\bm B\) 的列向量组的极大无关组分别为 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r}\) 和 \(\bm\beta_{j_1},\cdots,\bm\beta_{j_t}\),

则 \(\bm\alpha_1+\bm\beta_1,\cdots,\bm\alpha_n+\bm\beta_n\) 可被 \(\bm\alpha_{i_1},\cdots,\bm\alpha_{i_r},\bm\beta_{j_1},\cdots,\bm\beta_{j_t}\) 线性表出, 于是 \(\mathrm{rank}(\bm A+\bm B)\leq \mathrm{rank}(\bm A)+\mathrm{rank}(\bm B)\).

例 4.3.3: 设实矩阵 \(\bm A_{s\times n}\), 证明: \(\mathrm{rank}(\bm A'\bm A)=\mathrm{rank}(\bm A\bm A')=\mathrm{rank}(\bm A)\).

证法 1: 证明 \((\bm A'\bm A)\bm x=\bm0\) 与 \(\bm A\bm x=\bm0\) 同解.

若 \(\bm\eta\) 满足 \(\bm A\bm\eta=\bm0\), 显然 \(\bm A'\bm A\bm\eta=\bm0\).

若 \(\bm\eta\) 满足 \(\bm A'\bm A\bm\eta=\bm0\), 则 \(\bm\eta'\bm A'\bm A\bm\eta=(\bm A\bm\eta)'\bm A\bm\eta=\bm0\). 设 \(\bm A\bm\eta=(c_1,\cdots,c_n)'\), 则 \(\sum_{i=1}^n c_i^2=0\), 于是 \(\bm A\bm\eta=\bm0\).

两个方程组的解空间相同, 维度相等, 故 \(\mathrm{rank}(\bm A'\bm A)=\mathrm{rank}(\bm A)\).

另外 \(\mathrm{rank}(\bm A\bm A')=\mathrm{rank}(\bm A')=\mathrm{rank}(\bm A)\).

证法 2: 设 \(\mathrm{rank}(\bm A)=r\), 利用命题 4.3.1得:

\[\begin{aligned} \bm A\bm A'\begin{pmatrix}i_1,i_2,\cdots,i_r\\ i_1,i_2,\cdots,i_r \end{pmatrix}&=\sum_{1\leq k_1<\cdots<k_r\leq n} \bm A\begin{pmatrix}i_1,i_2,\cdots,i_r\\ k_1,k_2,\cdots,k_r \end{pmatrix} \bm A'\begin{pmatrix}k_1,k_2,\cdots,k_r\\ i_1,i_2,\cdots,i_r \end{pmatrix}\\ &=\sum_{1\leq k_1<\cdots<k_r\leq n} \bm A^2\begin{pmatrix}i_1,i_2,\cdots,i_r\\ k_1,k_2,\cdots,k_r \end{pmatrix} \end{aligned} \]

因 \(\bm A\) 有一个不为 0 的 \(r\) 阶子式, 故 \(\bm A\bm A'\) 也有一个不为 0 的 \(r\) 阶子式, 于是 \(\mathrm{rank}(\bm A\bm A')\geq r\).

同时 \(\mathrm{rank}(\bm A\bm A')\leq \mathrm{rank}(\bm A)=r\), 故 \(\mathrm{rank}(\bm A\bm A')=r\).

例 4.3.4: 行(列)向量组线性无关的矩阵称为行(列)满秩矩阵. 证明: 若 \(\bm A_{s\times n}\) 的秩为 \(r\), 则存在列满秩的 \(\bm B_{s\times r}\) 和行满秩的 \(\bm C_{r\times n}\), 使得 \(\bm A=\bm B\bm C\).

设 \(\bm A\) 行向量组的极大无关组为 \(\bm\gamma_{i_1},\cdots,\bm\gamma_{i_r}\), 则

\[\bm{A}=\begin{pmatrix} k_{11}\boldsymbol{\gamma}_{i_1}+k_{12}\boldsymbol{\gamma}_{i_2}+\cdots+k_{1r}\boldsymbol{\gamma}_{i_r}\\ k_{21}\boldsymbol{\gamma}_{i_1}+k_{22}\boldsymbol{\gamma}_{i_2}+\cdots+k_{2r}\boldsymbol{\gamma}_{i_r}\\ \vdots\\ k_{s1}\boldsymbol{\gamma}_{i_1}+k_{s2}\boldsymbol{\gamma}_{i_2}+\cdots+k_x\boldsymbol{\gamma}_{i_r} \end{pmatrix} =\begin{pmatrix} k_{11}&k_{12}&\cdots&k_{1r}\\ k_{21}&k_{22}&\cdots&k_{2r}\\ \vdots&\vdots&&\vdots\\ k_{s1}&k_{s2}&\cdots&k_{sr}\end{pmatrix} \begin{pmatrix}\boldsymbol{\gamma}_{i_1}\\ \boldsymbol{\gamma}_{i_2}\\ \vdots\\ \boldsymbol{\gamma}_{i_r} \end{pmatrix}=\bm B\bm C \]

显然 \(\bm C_{r\times n}\) 是行满秩矩阵, 而 \(r=\mathrm{rank}(\bm A)=\mathrm{rank}(\bm B\bm C)\leq \mathrm{rank}(\bm B)\), \(\bm B\) 只有 \(r\) 列, 故 \(\bm B\) 是列满秩矩阵.

例 4.3.6: 设 \(\bm A=(a_{ij})_{n\times m}\), 其中 \(a_{ij}=x_1^{i+j-2}+x_2^{i+j-2}+\cdots+x_n^{i+j-2}\), 证明 \(\displaystyle |\bm A|=\prod_{1\leq i<j\leq n} (x_j-x_i)^2\).

\(\displaystyle a_{ij}=\sum_{k=1}^n x_k^{i-1}x_k^{j-1}\), 故

\[\begin{aligned} |\bm A|&=\left| \begin{pmatrix} 1&1&\cdots&1\\ x_1&x_2&\cdots&x_n\\ \vdots&\vdots&&\vdots\\ x_1^{n-1}&x_2^{n-1}&\cdots&x_n^{n-1} \end{pmatrix} \begin{pmatrix} 1&x_1&\cdots&x_1^{n-1}\\1&x_2&\cdots&x_2^{n-1}\\ \vdots&\vdots&&\vdots\\ 1&x_n&\cdots&x_n^{n-1} \end{pmatrix} \right|\\ &=\prod_{1\leq i<j\leq n}(x_i-x_j)\cdot \prod_{1\leq i<j\leq n}(x_i-x_j)\\ &=\prod_{1\leq i<j\leq n} (x_j-x_i)^2 \end{aligned} \]

例 4.3.9: Cauchy 恒等式:

\[\left(\sum_{i=1}^n a_ic_i\right)\left(\sum_{i=1}^n b_id_i\right)-\left(\sum_{i=1}^n a_id_i\right)\left(\sum_{i=1}^n b_ic_i\right)=\sum_{1\leq j<k\leq n}(a_jb_k-a_kb_j)(c_jd_k-c_kd_j) \]

\[左边=\begin{vmatrix}\displaystyle\sum_{i=1}^n a_ic_i &\displaystyle\sum_{i=1}^n a_id_i\\ \displaystyle\sum_{i=1}^n b_ic_i &\displaystyle\sum_{i=1}^n b_id_i \end{vmatrix} =\left|\begin{pmatrix}a_1 &a_2 &\cdots &a_n\\ b_1 &b_2 &\cdots &b_n \end{pmatrix} \begin{pmatrix}c_1 & d_1\\ c_2 &d_2\\ \vdots&\vdots\\ c_n &d_n \end{pmatrix} \right| \]

由Binet-Cauchy 公式得:

\[上式=\sum_{1\leq j<k\leq n}\begin{vmatrix}a_j &a_k\\ b_j &b_k \end{vmatrix}\begin{vmatrix}c_j &d_j\\ c_k &d_k \end{vmatrix}= \sum_{1\leq j<k\leq n}(a_jb_k-a_kb_j)(c_jd_k-c_kd_j) \]

例 4.3.10: Cauchy-Schwarz-Bunyakovsky 不等式: \(\forall a_i,b_i\in\R\),

\[\sum_{i=1}^n a_i^2\cdot \sum_{i=1}^n b_i^2\geq \left(\sum_{i=1}^n a_ib_i\right)^2 \]

等号成立当且仅当 \((a_1,\cdots,a_n)\) 与 \((b_1,\cdots,b_n)\) 线性相关.

由例 4.3.9 得到 (这是 Lagrange 恒等式)

\[\sum_{i=1}^n a_i^2\cdot \sum_{i=1}^n b_i^2- \left(\sum_{i=1}^n a_ib_i\right)^2=\sum_{1\leq j<k\leq n} (a_jb_k-a_kb_j)^2\geq0 \]

等号成立当且仅当 \(\forall 1\leq j<k\leq n\), \(a_jb_k-a_kb_j=0\), 即 \(\mathrm{rank}\left(\begin{pmatrix}a_1&a_2&\cdots&a_n\\ b_1&b_2&\cdots&b_n\end{pmatrix}\right)\leq1\), 即 \((a_1,\cdots,a_n)\) 与 \((b_1,\cdots,b_n)\) 线性相关.

例 4.3.15: 设 \(\bm A\) 是 2 阶矩阵, \(k>2\), 证明: \(\bm A^k=\bm0\) 当且仅当 \(\bm A^2=\bm0\).

\((\Leftarrow)\) 显然. \((\Rightarrow)\) 若 \(\bm A^k=\bm0\), 则 \(|\bm A|=\bm0\), 于是 \(\mathrm{rank}(\bm A)\leq 1\).

当 \(\mathrm{rank}(\bm A)=0\) 时, \(\bm A=\bm0\), 显然 \(\bm A^2=\bm0\).

当 \(\mathrm{rank}(\bm A)=1\) 时, 设 \(\bm A=\begin{pmatrix} a &b \\ka &kb \end{pmatrix}=\begin{pmatrix}1\\k \end{pmatrix}(a,b)\), 故 \(\bm A^2=\begin{pmatrix}1\\k \end{pmatrix} (a+bk) (a,b)=(a+bk)\bm A\).

于是 \(\bm A^k=(a+bk)^{k-1}\bm A=\bm0\), 从而 \(a+bk=0\), 于是 \(\bm A^2=\bm0\).

习题 4.3.4: 证明: 对任意实矩阵 \(\bm A_{s\times n}\), 都有 \(\mathrm{rank}(\bm A\bm A'\bm A)=\mathrm{rank}(\bm A)\).

一方面 \(\mathrm{rank}(\bm A\bm A'\bm A)\leq \mathrm{rank}(\bm A)\),

同时 \(\mathrm{rank}(\bm A\bm A'\bm A)\geq \mathrm{rank}(\bm A\bm A'\bm A\bm A')=\mathrm{rank}[(\bm A\bm A')'(\bm A\bm A')]=\mathrm{rank}(\bm A\bm A')=\mathrm{rank}(\bm A)\). (利用例 4.3.3)

于是 \(\mathrm{rank}(\bm A\bm A'\bm A)=\mathrm{rank}(\bm A)\).

习题 4.3.7: 举例说明: 对复矩阵, \(\mathrm{rank}(\bm A'\bm A)\neq \mathrm{rank}(\bm A)\).

设 \(\bm A=\begin{pmatrix} i &1\\ 1 &-i \end{pmatrix}\), 则 \(\bm A'\bm A=\bm0\).

习题 4.3.10: 利用 Binet-Cauchy 公式计算:

\[|\bm A|=\begin{vmatrix} 1+x_1y_1&1+x_1y_2&\cdots&1+x_1y_n\\ 1+x_2y_1&1+x_2y_2&\cdots&1+x_2y_n\\ \vdots&\vdots&&\vdots\\ 1+x_ny_1&1+x_ny_2&\cdots&1+x_ny_n \end{vmatrix} \]

\[|\bm A|=\left|\begin{pmatrix}1 &x_1\\ 1&x_2\\ \vdots&\vdots\\ 1&x_n \end{pmatrix} \begin{pmatrix}1 &1&\cdots &1\\ y_1&y_2&\cdots&y_n \end{pmatrix} \right| \]

当 \(n>2\) 时, \(|\bm A|=0\);

当 \(n=2\) 时, \(|\bm A|=(x_2-x_1)(y_2-y_1)\);

当 \(n=1\) 时, \(|\bm A|=1+x_1y_1\).

例 4.3.11: 计算 \(n+1\) 阶行列式:

\[|\bm A|=\begin{vmatrix} (a_0+b_0)^n&(a_0+b_1)^n&\cdots&(a_0+b_n)^n\\ (a_1+b_0)^n&(a_1+b_1)^n&\cdots&(a_1+b_n)^n\\ \vdots&\vdots&&\vdots\\ (a_n+b_0)^n&(a_n+b_1)^n&\cdots&(a_n+b_n)^n \end{vmatrix} \]

\(\bm A_{(i+1,j+1)}=(a_i+b_j)^n=a_i^n+C_n^1 a_i^{n-1}b_j+\cdots+b_j^n\), 于是

\[\begin{aligned} |\bm A|&=\left|\begin{pmatrix}a_0^n&C_n^1a_0^{n-1}&\cdots&C_n^{n-1}a_0&1\\ a_1^n&C_n^1a_1^{n-1}&\cdots&C_n^{n-1}a_1&1\\ \vdots&\vdots&&\vdots&\vdots \\ a_n^n&C_n^1a_n^{n-1}&\cdots&C_n^{n-1}a_n&1 \end{pmatrix}_{(n+1)\times (n+1)} \begin{pmatrix} 1&1 &\cdots &1\\ b_0&b_1 &\cdots &b_n\\ \vdots&\vdots&&\vdots \\ b_0^n &b_1^n &b_n^n \end{pmatrix}_{(n+1)\times (n+1)} \right|\\ &=\prod_{k=0}^n C_n^k \prod_{1\leq i<j\leq n} (a_j-a_i)(b_j-b_i) \end{aligned} \]

例 4.3.12: 计算 \(n\) 阶行列式:

\[|\bm{A}|=\begin{vmatrix} \cos(\theta_1-\varphi_1)&\cos(\theta_1-\varphi_2)&\cdots&\cos(\theta_1-\varphi_n)\\ \cos(\theta_2-\varphi_1)&\cos(\theta_2-\varphi_2)&\cdots&\cos(\theta_2-\varphi_n)\\ \vdots&\vdots&&\vdots\\ \cos(\theta_n-\varphi_1)&\cos(\theta_n-\varphi_2)&\cdots&\cos(\theta_n-\varphi_n) \end{vmatrix} \]

\(\bm A_{(i,j)}=\cos(\theta_i-\varphi_j)=\cos\theta_i\cos\varphi_j+\sin\theta_i\sin\varphi_j\), 于是

\[|\bm A|=\left|\begin{pmatrix} \cos\theta_1 &\sin\theta_1\\ \cos\theta_2 &\sin\theta_2\\ \vdots&\vdots\\ \cos\theta_n &\sin\theta_n \end{pmatrix}\begin{pmatrix} \cos\varphi_1 &\cos\varphi_2 &\cdots &\cos\varphi_n\\ \sin\varphi_1 &\sin\varphi_2 &\cdots &\sin\varphi_n \end{pmatrix} \right| \]

当 \(n>2\) 时, \(|\bm A|=0\);

当 \(n=2\) 时, \(|\bm A|=\sin(\theta_2-\theta_1)\sin(\varphi_2-\varphi_1)\);

当 \(n=1\) 时, \(|\bm A|=\cos(\theta_1-\varphi_1)\).

例 4.3.14: 设 \(\bm A_{s\times n}\), \(\bm B_{n\times m}\), 证明: \(\mathrm{rank}(\bm A\bm B)=\mathrm{rank}(\bm B)\) 当且仅当 \((\bm A\bm B)\bm x=\bm0\) 的解都是 \(\bm B\bm x=\bm0\) 的解.

\((\Leftarrow)\) 设 \((\bm A\bm B)\bm x=\bm0\) 的解都是 \(\bm B\bm x=\bm0\) 的解, 同时显然 \(\bm B\bm x=\bm0\) 的解也是 \((\bm A\bm B)\bm x=\bm0\) 的解,

故两个方程组的解空间相同, 于是 \(\dim W=m-\mathrm{rank}(\bm A\bm B)=m-\mathrm{rank}(\bm B)\), 即 \(\mathrm{rank}(\bm A\bm B)=\mathrm{rank}(\bm B)\).

\((\Rightarrow)\) 若 \(\mathrm{rank}(\bm A\bm B)=\mathrm{rank}(\bm B)\), 设两个方程组的解空间分别为 \(W_{AB}\) 和 \(W_B\), 则 \(\dim W_{AB}=\dim W_B\).

因为 \(\bm B\bm x=\bm0\) 的解是 \((\bm A\bm B)\bm x=\bm0\) 的解, 故 \(W_B\sube W_{AB}\). 由命题 3.4.5得 \(W_B=W_{AB}\).

例 4.3.16: 设 \(\bm A_{n\times n}\), 证明: 若 \(\exist m\in\Z^+\), 使得 \(\mathrm{rank}(\bm A^m)=\mathrm{rank}(\bm A^{m+1})\), 则 \(\forall k>0\), \(\mathrm{rank}(\bm A^m)=\mathrm{rank}(\bm A^{m+k})\).

对 \(k=1\), 已有 \(\mathrm{rank}(\bm A^m)=\mathrm{rank}(\bm A^{m+1})\), 设对 \(k\) 及更小的正整数有 \(\mathrm{rank}(\bm A^m)=\mathrm{rank}(\bm A^{m+k})\),

令 \(\bm A^{m+k+1}\bm x=\bm0\Longrightarrow \bm A^{k+m}(\bm A\bm x)=\bm0\), 即 \(\bm y=\bm A\bm x\) 是 \(\bm A^{k+m}\bm y=\bm0\) 的解,

因为 \(\mathrm{rank}(\bm A^{m+k-1})=\mathrm{rank}(\bm A^{m+k})\), 由例 4.3.14得 \(\bm y\) 也是 \(\bm A^{k+m-1}\bm y=\bm0\) 的解, 即 \(\bm A^{k+m}\bm x=\bm0\) 的解,

故 \(\bm A^{m+k+1}\bm x=\bm0\) 的解也是 \(\bm A^{m+k}\bm x=\bm0\) 的解, 于是 \(\mathrm{rank}(\bm A^{m+k+1})=\mathrm{rank}(\bm A^{m+k})\).

‍

‍