P8478 「GLR-R3」清明
参考了出题人题解和 xcyyyyyy 大神的题解,强推前两篇。
拿到题完全没思路怎么办???
人类智慧的巅峰,思维量的登峰造极。
换句话说就是非人题目,不过不得不说 GLR 的题是真的好,难度也是真的高。
首先我们需要看懂题面,这是第一个难点。
题面大意如下:
对于一个雨滴,它可以向任意编号小于等于 \(\min\{i+k,n\}\) 的台阶上移动,而其对应的一部分容量也会在移动后修改至其移动后的台阶。
同时雨滴体积不会莫名其妙减少或者增多。
而在「下一个瞬间」其对应的奇妙度为 \(\prod\limits_{i=1}^{n}a_i'\)。
求所有本质不同的「下一个瞬间」的奇妙度总和。
考虑从数据范围入手。
-
Subtask 5
对于 \(k=1\),在此情况下每个台阶上的雨滴最多只会向下移动一个台阶。
我们定义 \(c_i\) 为第 \(i\) 个台阶向下一阶流动的雨水容量。
那么我们就可以知道 \(a_i'=a_i+c_{i-1}-c_i\)。
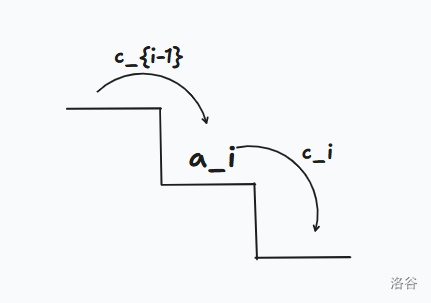
可以发现 \(ans=\sum\limits_{c}\prod\limits_{i=1}^{n}(a_i+c_{i-1}-c_i)\)。
考虑多项式展开,对于内部的 \(a_i+c_{i-1}-c_i\) 我们直接划分为两部分:\(a-c_i\) 和 \(c_{i-1}\)。
此时我们推广到积就会得到很多项 \(a-c_i\) 和 \(c_{i-1}\) 的和,我们再引入一个子集 \(S\subseteq\{1,2,3,\cdots,n\}\)。
每个 \(i\in S\) 代表在 \(a_i-c_i\) 中选取,否则代表在 \(c_{i-1}\) 中选取。
那么我们也就发现 \(\prod\limits_{i=1}^{n}(a_i+c_{i-1}-c_i)=\sum\limits_{S\subseteq \{1,2,\cdots,n\}}\prod\limits_{i\in S} (a_i-c_{i})\prod\limits_{i\not\in S}c_{i-1}\)。
整体式子也就得到了 \(ans=\sum\limits_{c}\sum\limits_{S\subseteq \{1,2,\cdots,n\}}\prod\limits_{i\in S} (a_i-c_{i})\prod\limits_{i\not\in S}c_{i-1}\)。
我们考虑去掉外层的 \(\sum\limits_{c}\),策略就是把下标 \(c_i\) 相同的一批都合成到一起。
当 \(i<n\) 时,考虑 \(i\) 和 \(i-1\) ,定义 \(f_{i,1}\) 为包含 \(i\) 的所有 \(S\) 的乘积之和,\(f_{i,1}\) 为不包含 \(i\) 的所有 \(S\) 的乘积之和,我们就可以分成 \(4\) 个情况来转移。
-
\(i - 1 \in S, i \in S\)
贡献是 \(\sum\limits_{0\le c_i \le a_i}(a_i-c_i)=\frac{a_i(a_i+1)}{2}\)。
-
\(i - 1 \not \in S, i \in S\)
贡献是 \(\sum\limits_{0\le c_i \le a_i} 1 = a_i+1\)。
-
\(i - 1 \in S, i \not \in S\)
贡献是 \(\sum\limits_{0\le c_i \le a_i}(a_i-c_i)c_i = \frac{a_i^2(a_i+1)}{2}-\frac{a_i(a_i+1)(2a_i+1)}{6} = \frac{(a_i-1)a_i(a_i+1)}{6}\)。
-
\(i - 1 \not \in S, i \not \in S\)
贡献是 \(\sum\limits_{0\le c_i \le a_i}c_i=\frac{a_i(a_i+1)}{2}\)。
那么我们就可以直接递推的从 \(f_{i-1,0/1}\) 向 \(f_{i,0/1}\) 转移。
这样我们就终于完成了拿到了 13 pts,复杂度 \(O(n)\)。
-
-
Subtask 6
考虑从 Sub5 进行推广, \(c_i \to c_{i,j}\) 代表第 \(i\) 个台阶到第 \(i+j\) 个台阶流动的量,然后就能拿到一个能拆的式子。
\[\sum_{c}\prod_{i=1}^{n}\left(\sum_{j=0}^{\min(i-1,k)}c_{i-j,j}\right) \]然后再推好像就好点,我们继续展开。
依然是先把 \(\sum\limits_c\) 置之不理。
我们设对于所有 \(c_{i,j}\) 的出现下标构成的集合为 \(S_i\),那么可以得到这样一个式子。
\[\prod_{i=1}^n\prod_{j\in S_i}c_{i,j} \]考虑外层 \(\sum_{c}\) 的影响,显然第一维不同的 \(c\) 之间互不影响。
先将外层乘积 \(\prod_{i=1}^{n}\) 展开为若干 \(n\) 次单项式的和,针对每个单项式,我们考虑 \(c_{i,j}\) 的约束即 \(\sum_j c_{i,j} = a_i\)。
利用乘法分配律,分别对每个 \(i\) 维度的 \(c_{i,j}\) 进行求和,最终我们可以收拢成一个和式。
\[\prod_{i=1}^n\sum_{c_i}\left[\sum_{j}c_{i,j}=a_i\right]\prod_{j\in S_i}c_{i,j} \]这好像不是很好做啊,那我们可以构建一个组合意义来简化题面。
我们用 \(r_i\) 表示对于任意合法的 \(j\),\(c_{i,j}\) 中有 \(r_i\) 个变量可以取到非 \(0\) 值,也就是说 \(r_i=\min(n-i,k)+1\)。
那么我们就可以建立这样的模型:
有编号为 \(0,1,2,\dots,r_i-1\) 的 \(r_i\) 个盒子。
其中编号落在属于 \(S_i\) 的盒子,放了 \(x\) 个球会贡献 \(x\)。
而其它盒子无论放多少个球,贡献都是 \(1\)。
一种方案的贡献为各个盒子的贡献的积。
求往 \(r_i\) 个盒子中任意放 \(a_i\) 个没有任何区别的球的贡献之和。
虽然还是不好做,但是起码可以构建生成函数了不是吗?
我们可以发现我们并不关心 \(S_i\) 具体是多少,我们只关心 \(|S_i|\)。
我们构造生成函数来实现,对于编号在 \(S_i\) 中的盒子,这些盒子的特点是放 \(x\) 个球的贡献是 \(x\),生成函数为 \(\frac{x}{(1-x)^2}\),将球放进盒子时,贡献会随着球的数目成比例增加。
剩下的盒子,这些盒子的特点是不论放多少球,贡献始终为 \(1\),因此其生成函数为 \(\frac{1}{1-x}\),球的数目对贡献无影响,但我们仍然允许球被放进去。
将这些生成函数组合在一起,让 \(|S_i| = s_i\),那么总生成函数为:
\[G(x) = \left( \frac{x}{(1 - x)^2} \right)^{s_i} \cdot \left( \frac{1}{1 - x} \right)^{r_i - s_i} \]简化得到:
\[G(x) = \frac{x^{s_i}}{(1 - x)^{s_i + r_i}} \]为了求往 \(r_i\) 个盒子中放入 \(a_i\) 个球的贡献,我们需要找到生成函数 \(G(x)\) 中 \(x^{a_i}\) 的系数:
\[ [x^{a_i}] G(x) = [x^{a_i}] \frac{x^{s_i}}{(1 - x)^{s_i + r_i}} \]这等价于:
\[ [x^{a_i - s_i}] \frac{1}{(1 - x)^{s_i + r_i}} \]对 \(\frac{1}{(1-x)^{s_i + r_i}}\) 展开,得到:
\[\frac{1}{(1-x)^{s_i + r_i}} = \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^n \]将这一展开式代入 \(G(x)\) 中:
\[\begin{aligned} G(x) &= x^{s_i} \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^n\\ &= \sum_{n=0} \binom{n + s_i + r_i - 1}{s_i + r_i - 1} x^{n + s_i} \end{aligned} \]为了找到 \(x^{a_i}\) 项,需要满足 \(n + s_i = a_i\),可以得知 \(n = a_i - s_i\)。
代入可以得到 \(x^{a_i}\) 项的系数为:
\[\binom{(a_i - s_i) + s_i + r_i - 1}{s_i + r_i - 1} = \binom{a_i + r_i - 1}{s_i + r_i - 1} \]可以发现结果只受到 \(S_i\) 的影响,上面已经提到了,我们考虑 \(s_i\) 是怎么来的。
可以发现每个 \(i\) 会向集合 \(\max\{i-k,1\} \le j \le i\) 的某个盒子 \(j\) 恰好贡献 \(S_j\)。
因此每个 \(i\) 在对应区间内,只会贡献一次。
每个 \(i\) 的贡献可以由多个位置 \(j \in (i,i+k)\) 贡献,可以反过来理解:
实际上每个 \(s_i\) 可以从 \(\{i, i+1, \dots, i+r_i-1\}\) 这些位置中任选一个贡献。
进行 \(dp\) 即可,设 \(f_{i,j}\) 表示在后缀 \(i\) 中有 \(j\) 个位置没有贡献过 \(s\) 的权值和。
转移就枚举一下 \(s\) 然后组合数计算,复杂度 \(O(n^3)\)
-
Subtask 7
拓展 Subtask 6 中的处理方法,考虑状压。
设 \(f_{i,S}\),用 \(i\) 表示当前后缀,用 \(S\) 表示 \(i,i+1,i+2,\dots,\min(i+k,n)\) 是否已经都贡献过 \(s\),复杂度 \(O(n\cdot 3^k)\) 是过不去的。
那咋办?注意到 \(i\) 的贡献只和 \(S\) 中新增的已经贡献过的位置个数有关,并且能贡献到 \(S\) 的前驱状态 \(T\) 得满足 \(T\subseteq S\),因此我们可以直接做高维前缀和,同时记录一下新增个数即可。
复杂度 \(O(n\cdot k^2\cdot 2^k)\),可以通过 Subtask 7。
-
Subtask 8
直接莽 \(O(n\cdot k^2\cdot 2^k)\)!欸过不去,考虑优化。
发扬人类智慧,我们发现在 \(k\) 较大的时候只有较少的台阶会超出限制,大多数问题集中在一部分位置
我们如果在 \(k\) 和 \(k+1\) 处对前后分成两部分的话,枚举后半段位置是否被前半段占用,从而使得前后的贡献分开计算。这样每一段的内部贡献就独立了
因为前半段的贡献不会超出限制,因此每个内部后缀都可以贡献,问题转化为类似 Subtask 6 的形式
考虑动态规划, \(f_{i,j,S}\) 表示一下含义:
- \(i\): 从后缀 \(i\) 开始。
- \(j\): 在区间 \([i, k]\) 中,尚未被占用的位置数。
- \(S\): 表示区间 \((k, n]\) 中的位置占用情况。
然后根据前半段和后半段的不同情况分别处理。
我们对前半段的 \(j\) 做类似 Sub6 的转移,对 \(S\) 做类似 Sub7 的转移。
对于后半段,我们枚举 \(S\) 来做类似 Sub6 的转移。
复杂度为 \(O(n\cdot k^2\cdot \sqrt k\cdot 2^k)\)。
-
Subtask 9
Sub8 的做法又过不去了?
我们引入容斥思想来优化 Sub8 的做法,为了优化算法,我们枚举后半段 \((k+1,n]\) 中的位置是否被超出限制占用。
我们用状态 \(f_{i,j}\) 来表示后缀 \(i\) 中有 \(j\) 个位置是可选的但未被占用
在状态转移时,从 \(f_{i+1}\) 转移到 \(f_i\) 时,不仅要考虑位置 \(i\) 是否被加入,还需要考虑位置 \(i+k+1\) 是否被加入,和 Sub6 类似,但需要结合对后段的枚举。
这样我们就解决了 Sub9,复杂度 \(O(n^2\cdot k\cdot 2^{n-k})\)。
现在我们解决了所有的 Subtask,我们将 Sub7 和 Sub9 进行结合即可通过本题。