操作系统的定义:

用户接口(重要):
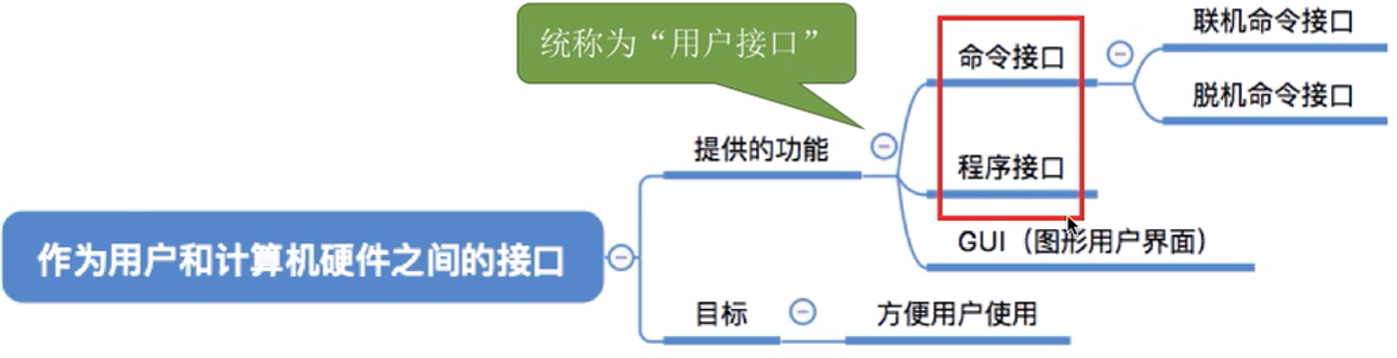
具体介绍

易懵概念:
系统调用 = 系统调用命令 = 广义指令
本节总结:
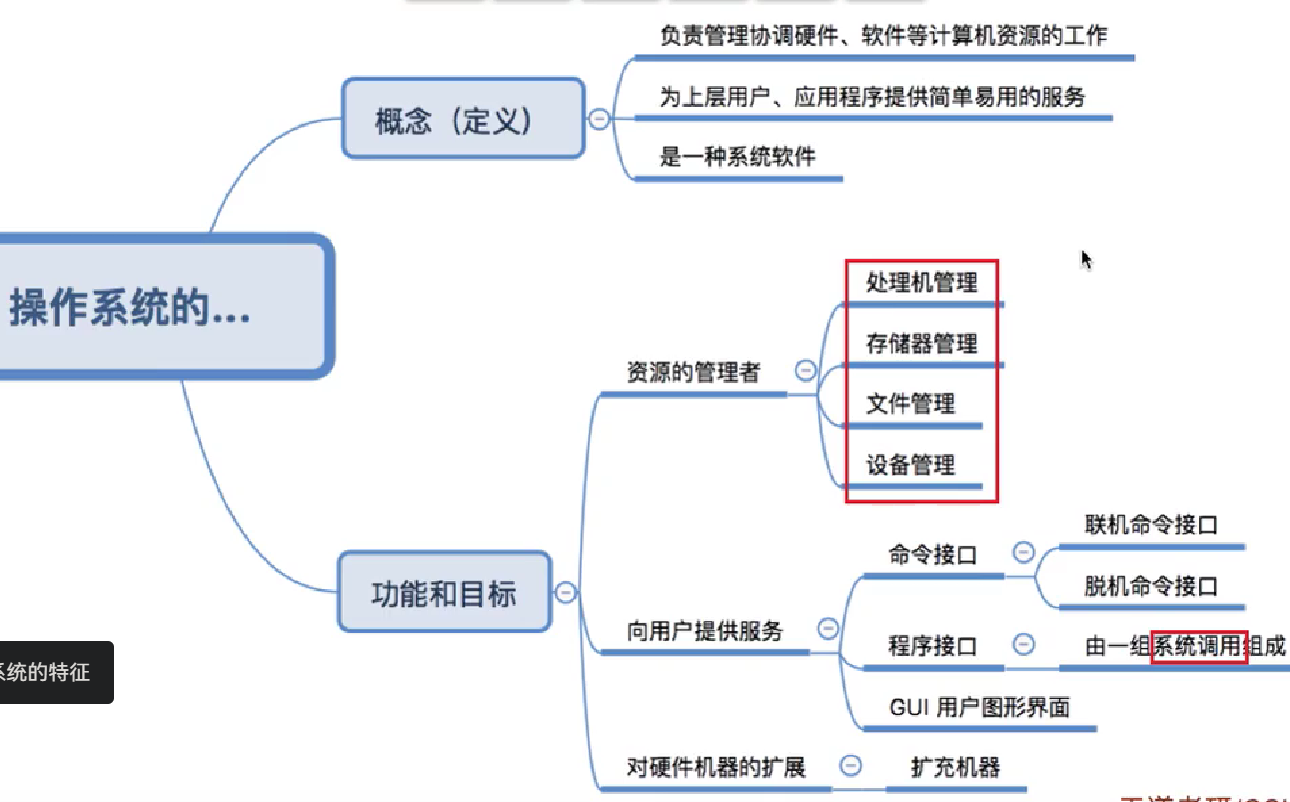
操作系统的特性--
1.共享
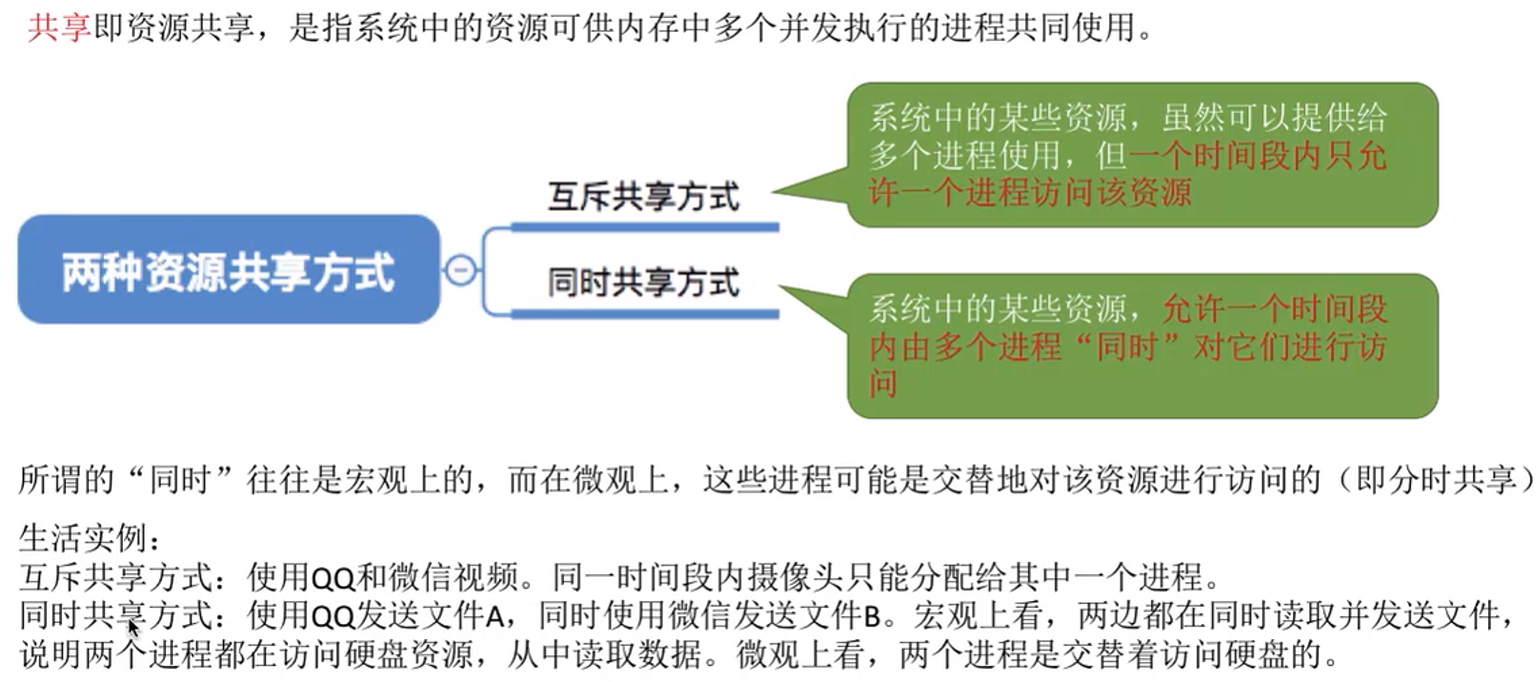
2.并发与共享之间的关系
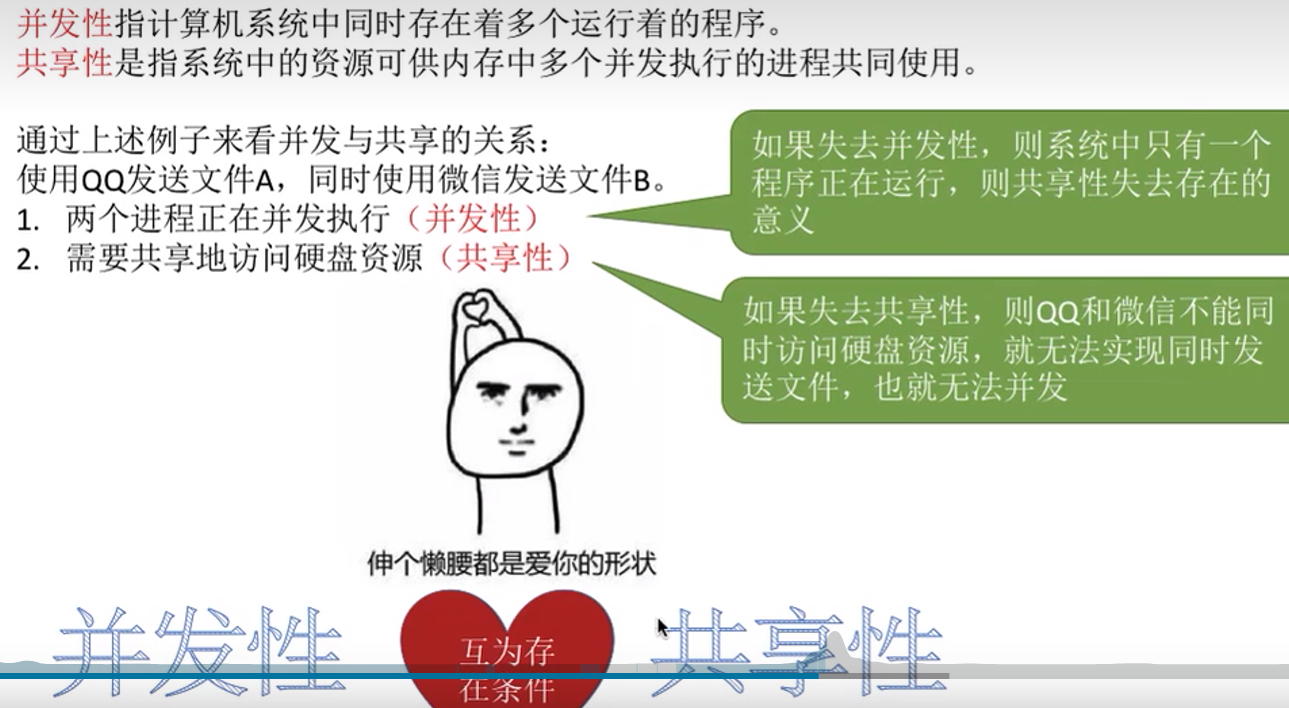
3.虚拟

4.异步

5.总结:
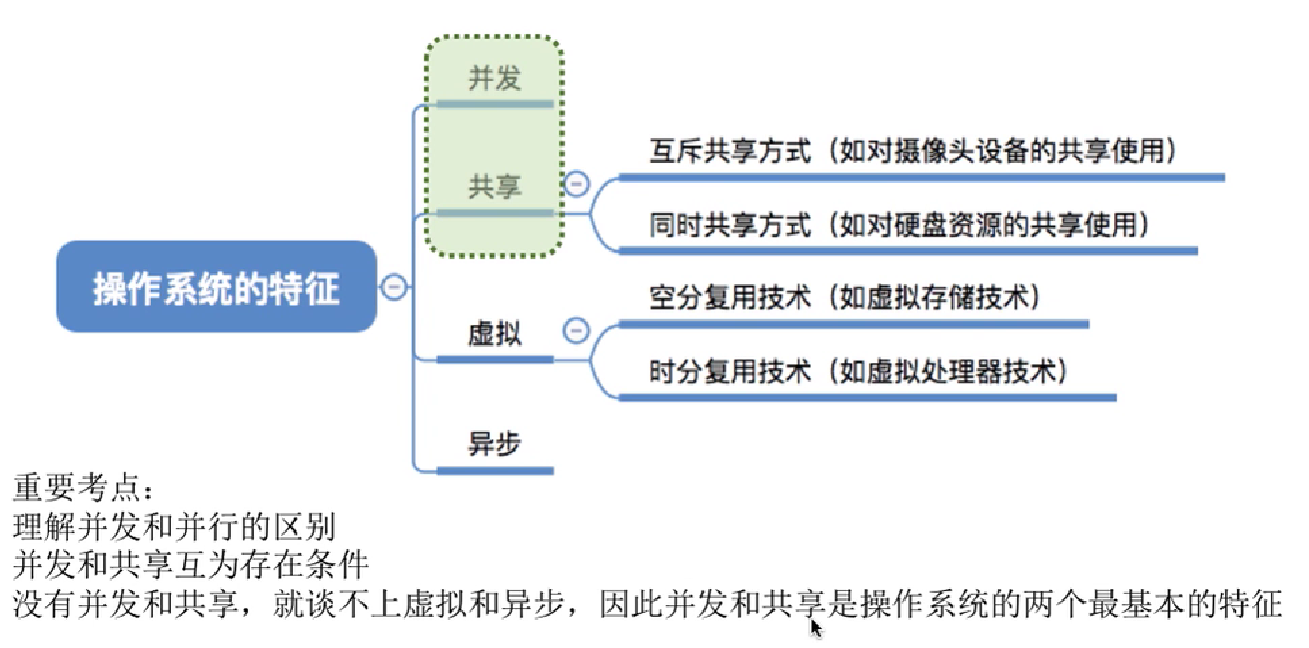
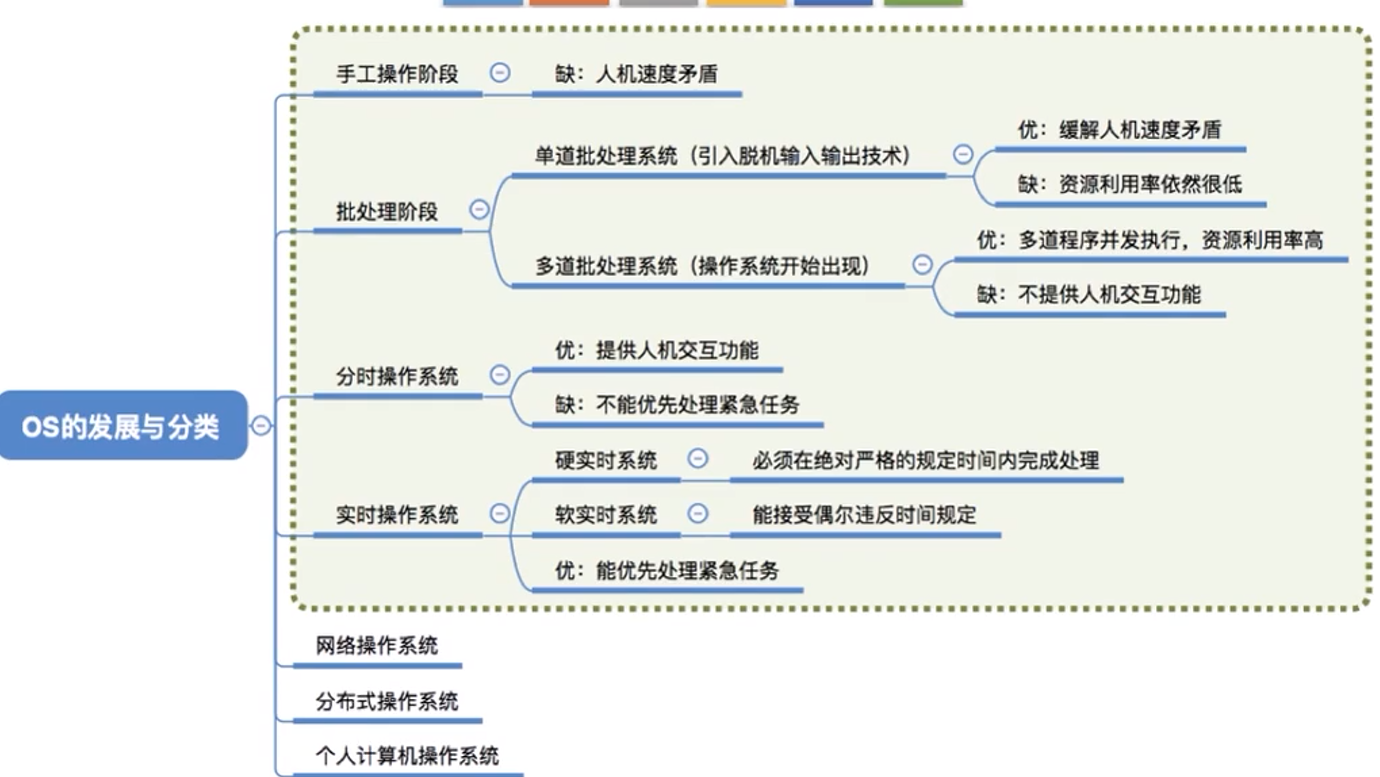
操作系统的发展与分类(框中的为重点):
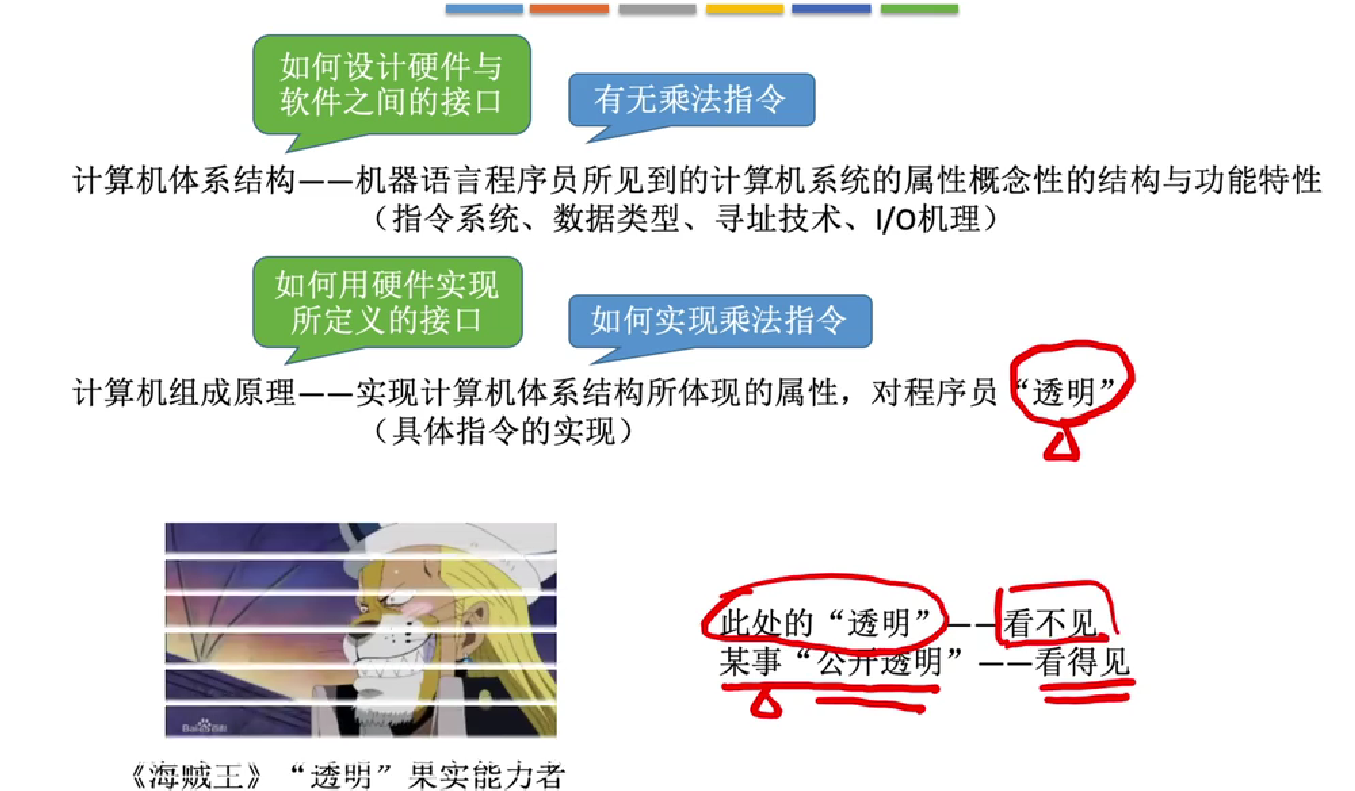
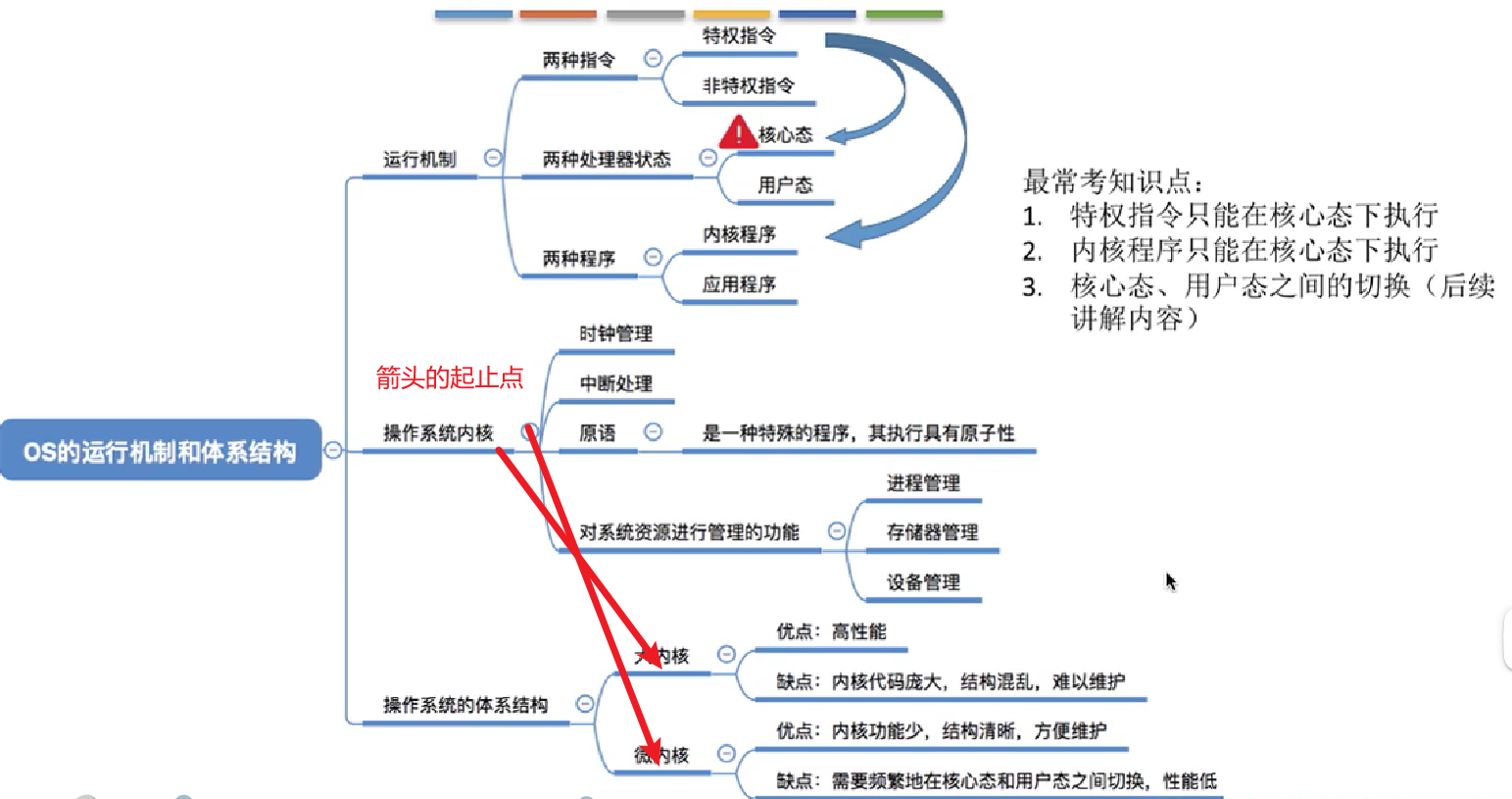
运行机制和体系结构:
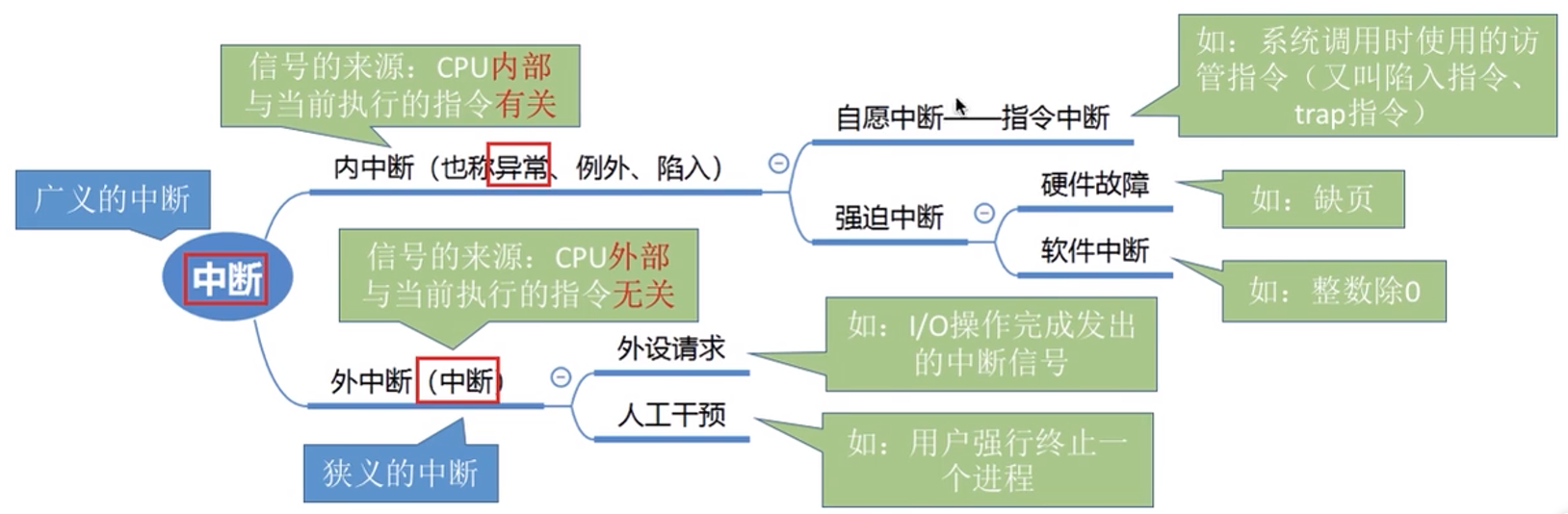
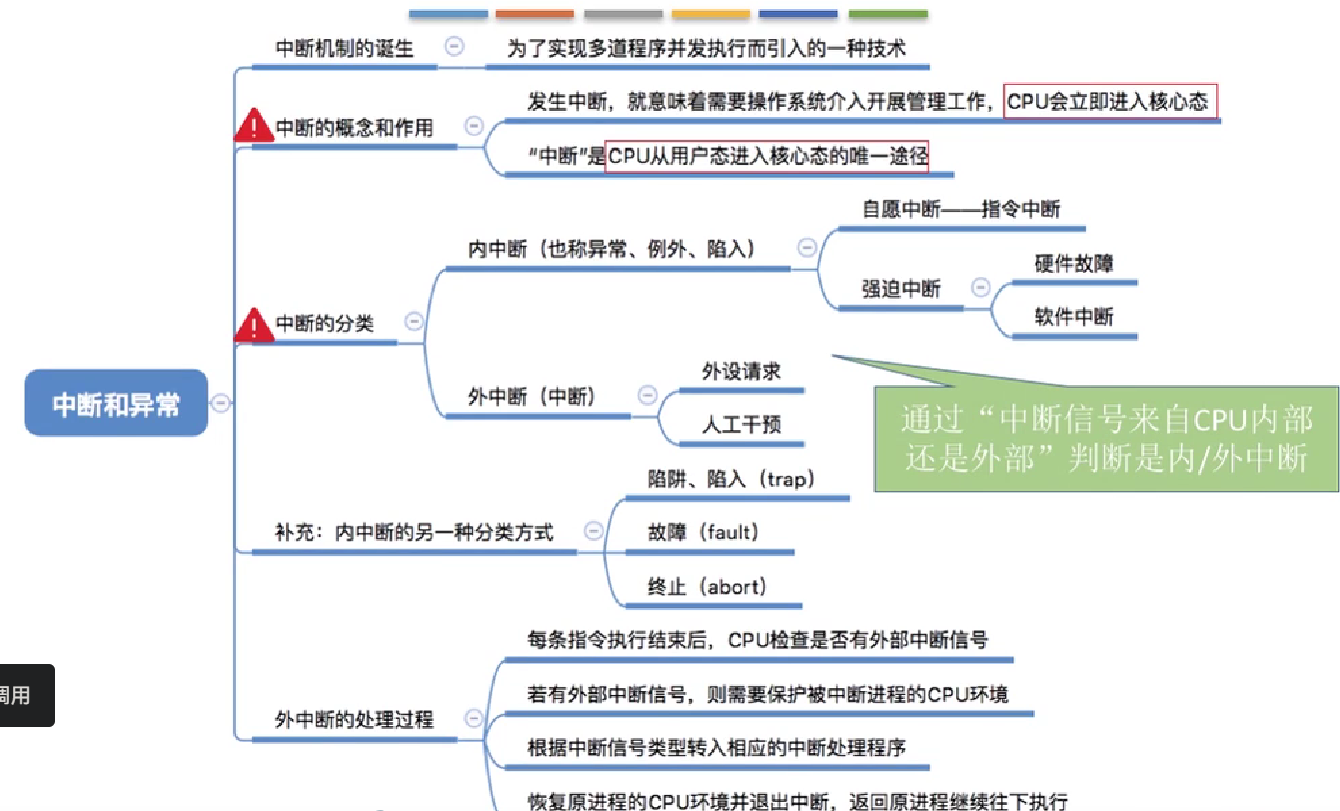
中断和异常:
中断的分类:
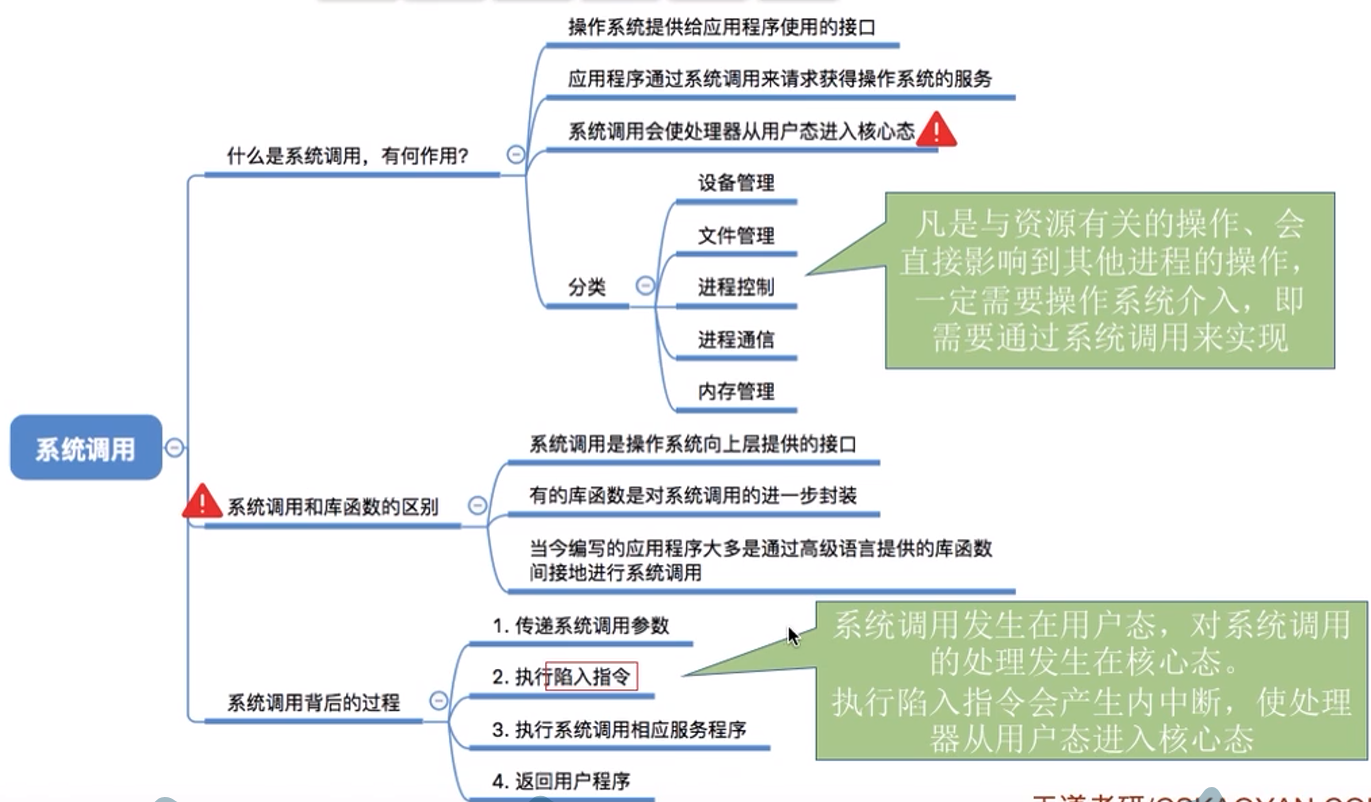
系统调用:
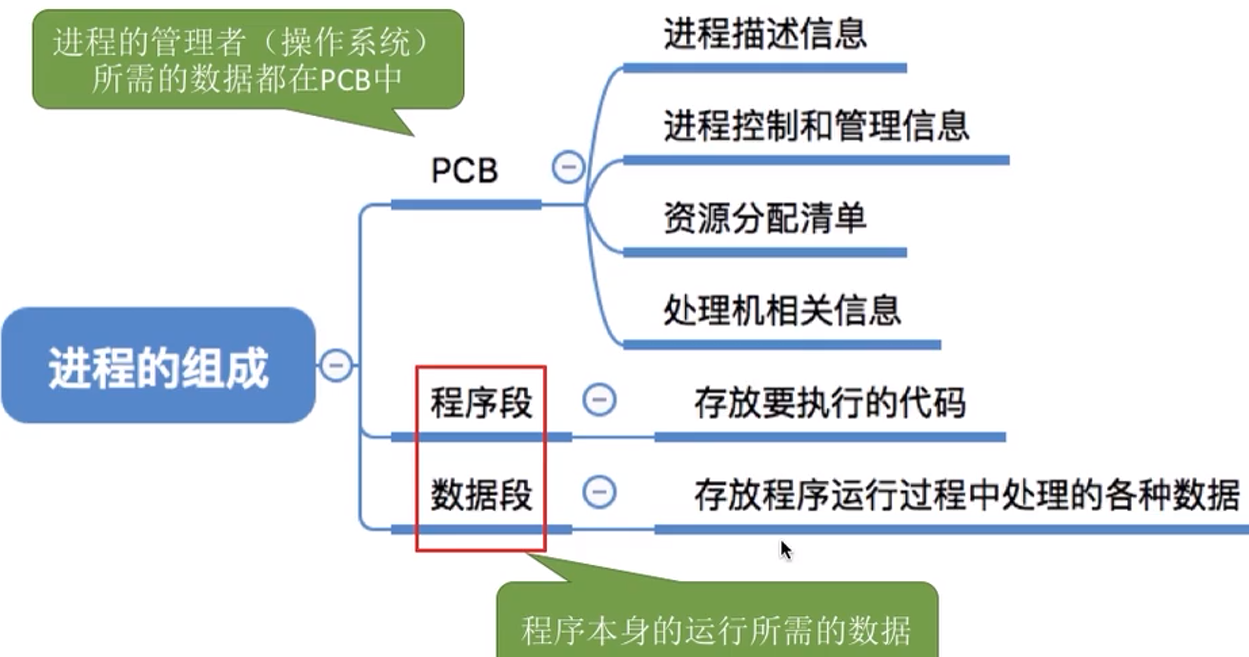
进程的定义、组成、组织方式、特征
组成:
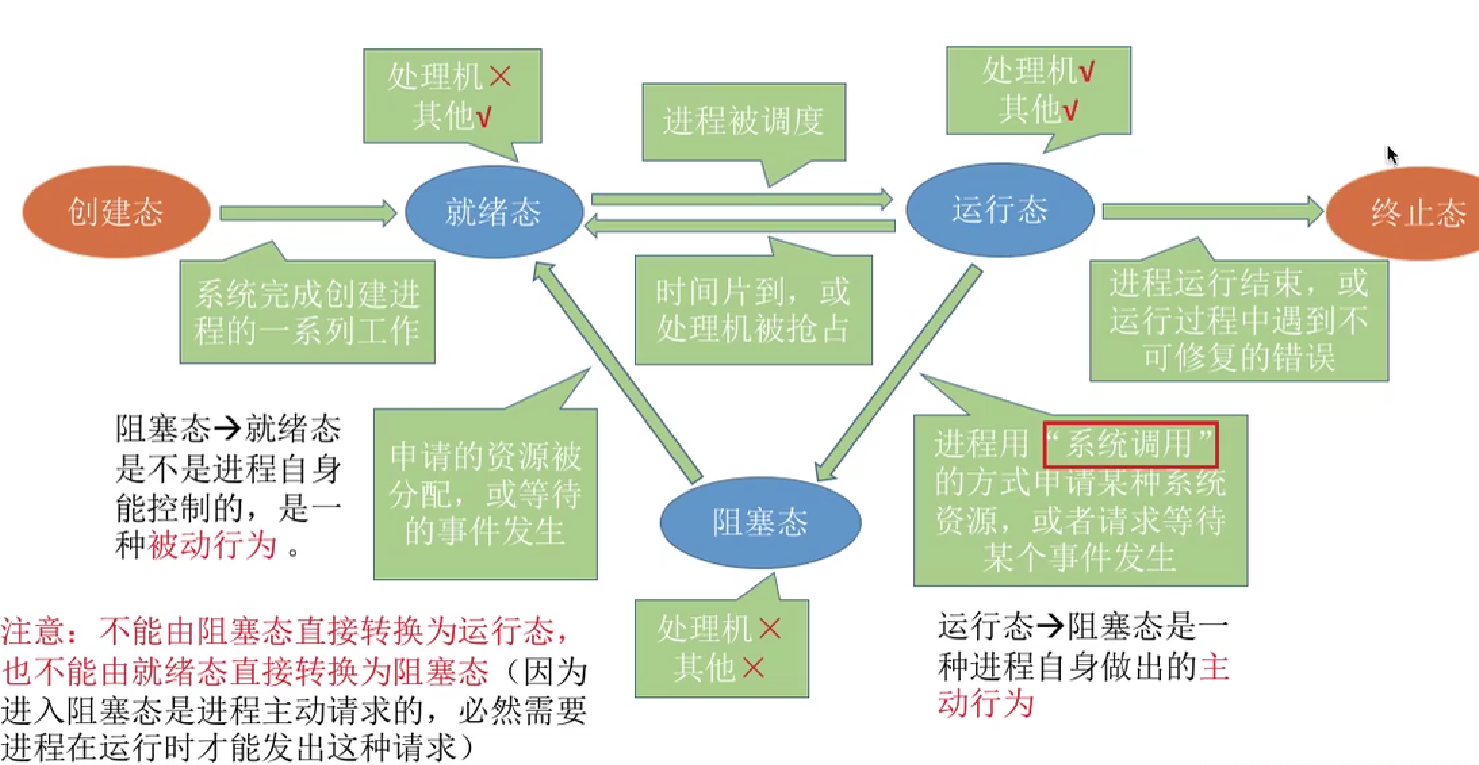
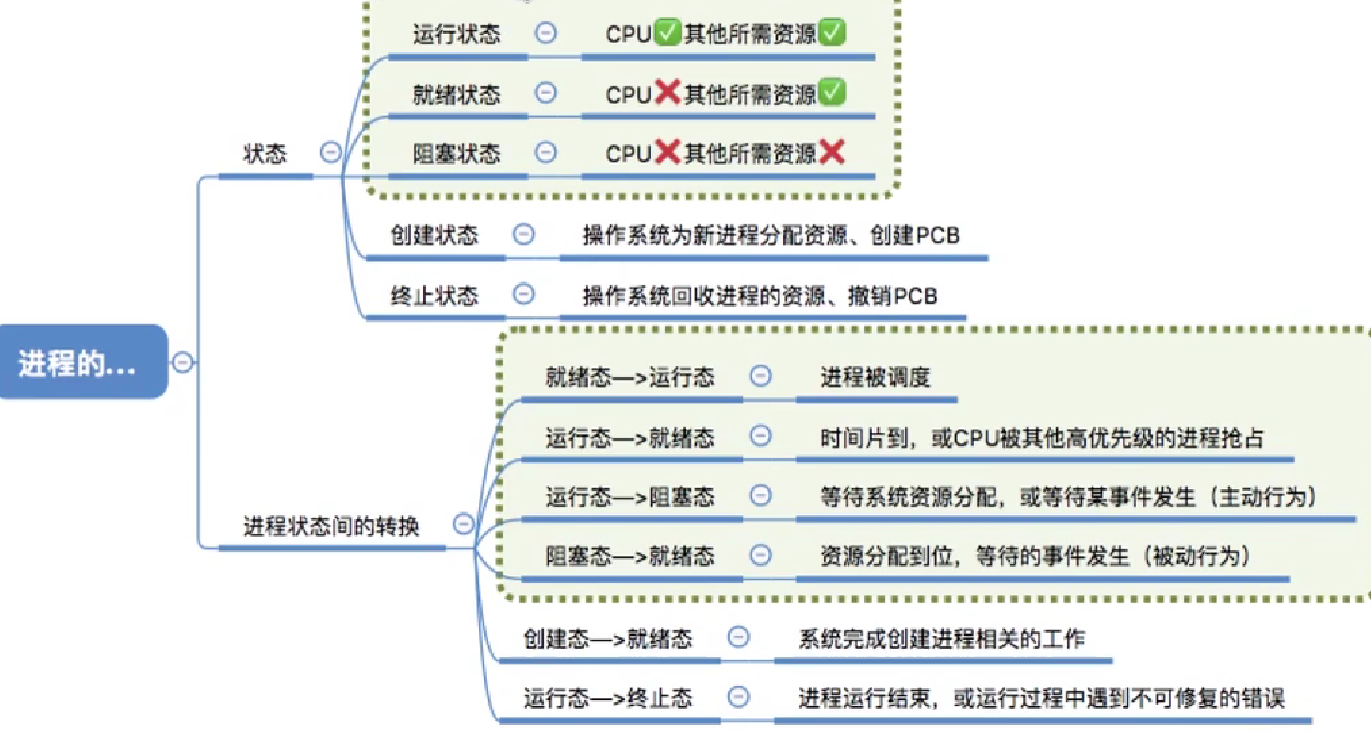
进程的状态与转换
:
小结:
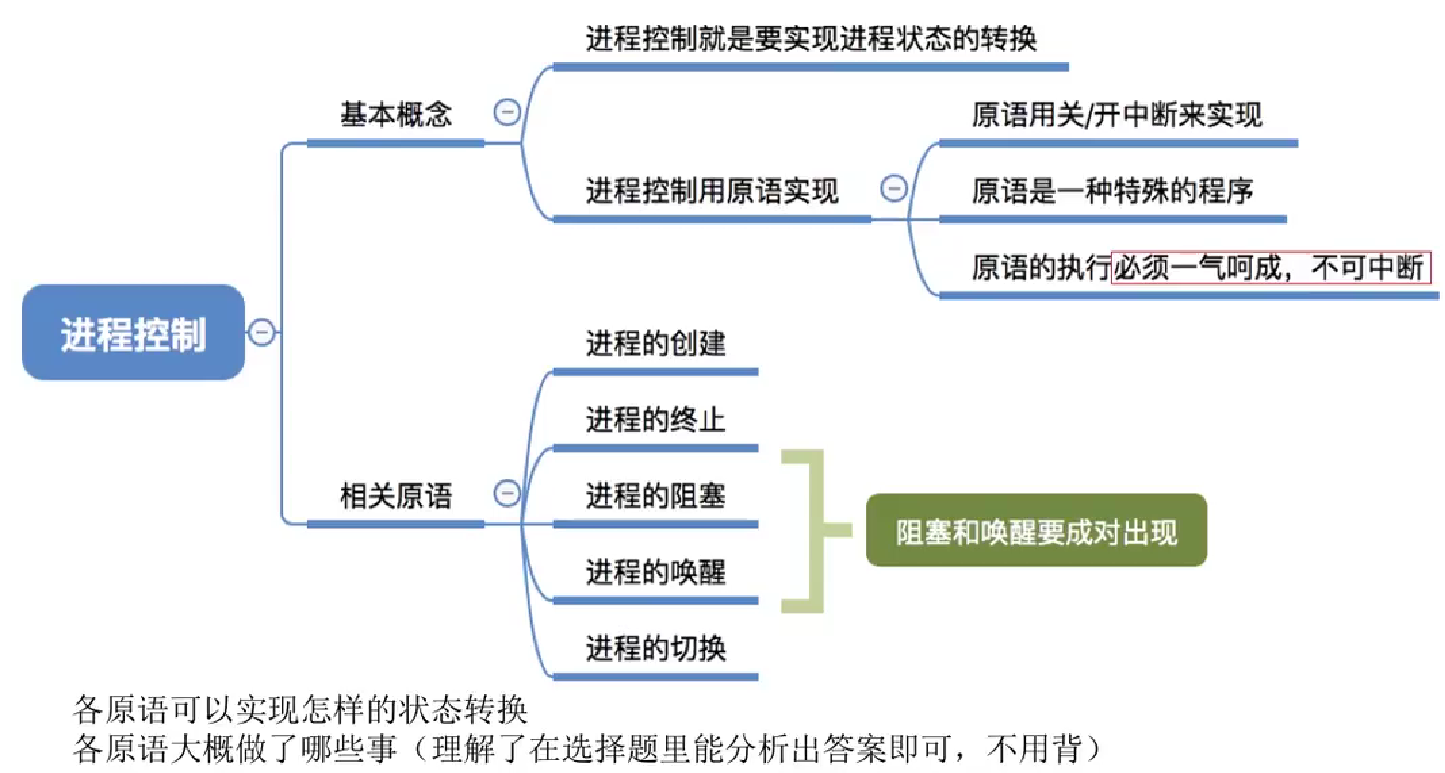
进程控制 原语的定义与分类
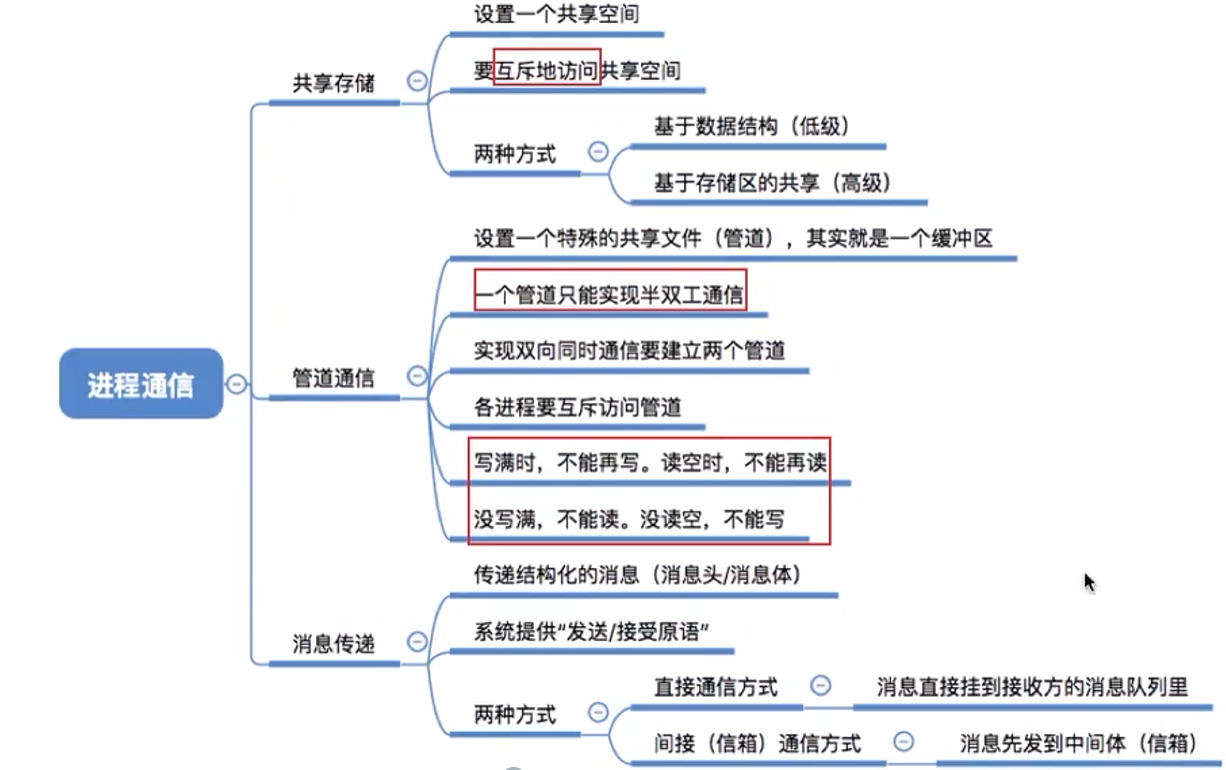
进程通信
主要讲了3个部分内容:共享存储;管道通信;信息传递
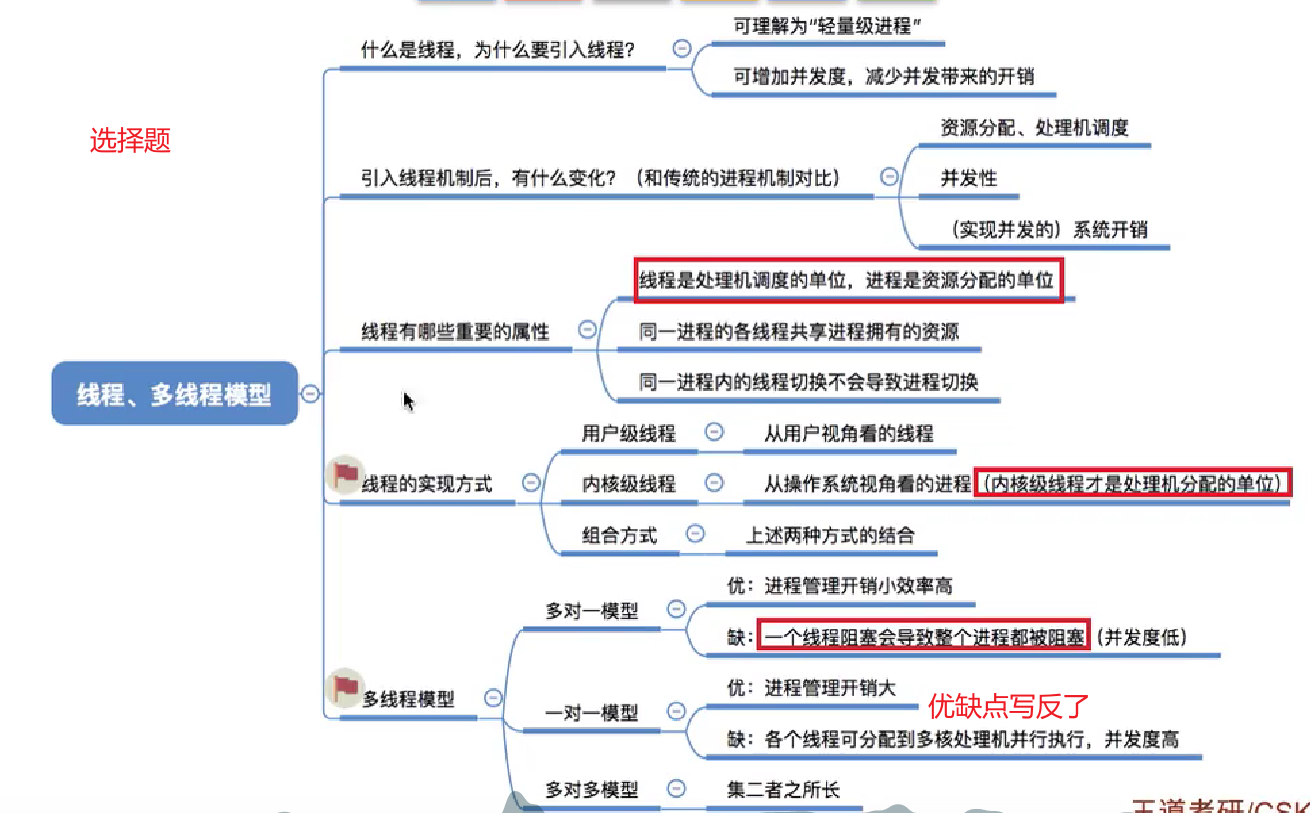
2.1_5_线程概念和多线程模型
线程和进程的重新定义;线程带来的优缺点;多线程模型;用户线程和核心线程的对应关系
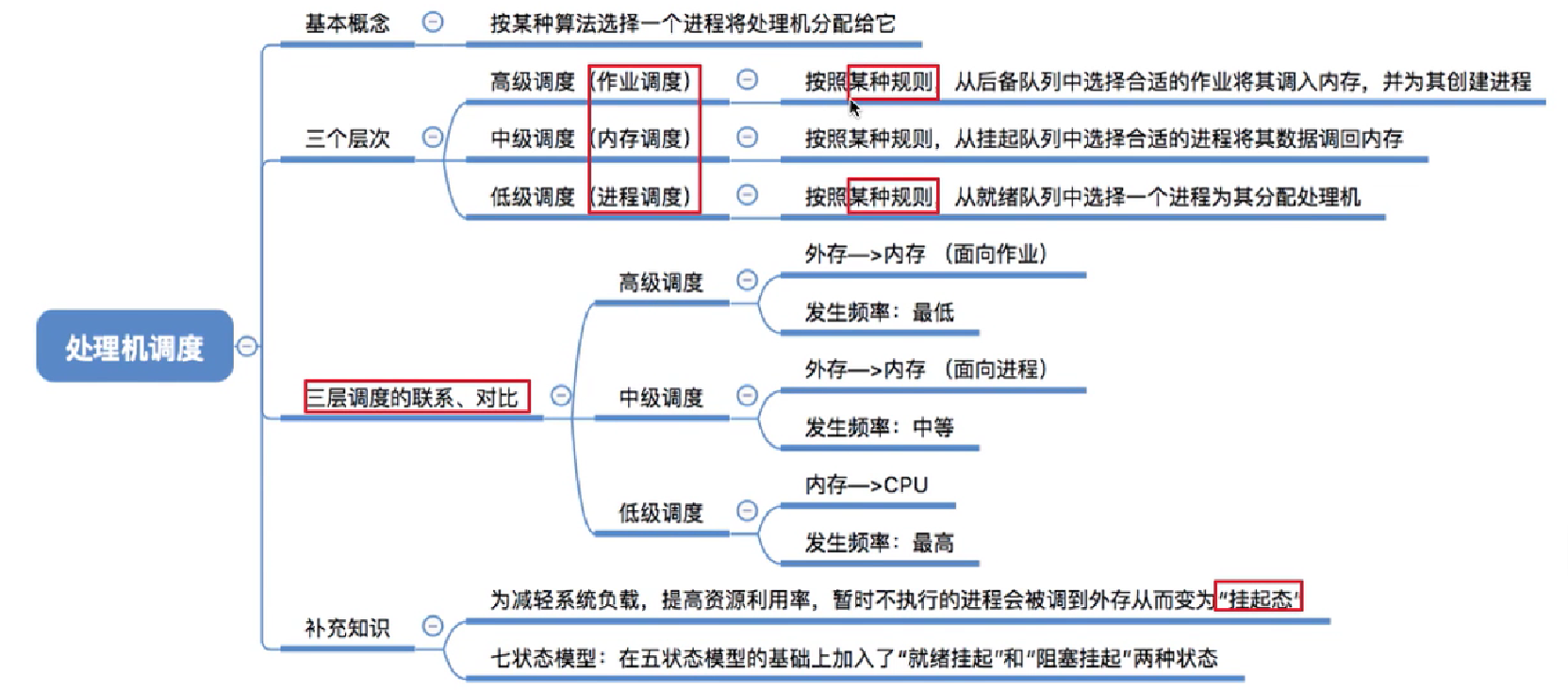
2.2_1_处理机调度的概念、层次
三种调度的层次;三层调度的联系与对比;进程的五状态模型;进程的七状态模型
2.2_2_进程调度的时机、切换与过程、方式
2.2_3_调度算法的评价指标
2.2_4_FCFS、SJF、HRRN调度算法
2.2_5_调度算法:时间片轮转、优先级、多级反馈队列
2.3_1_进程同步、进程互斥