T1 JOIRIS
你在玩俄罗斯方块,游戏区域是一个宽度为 \(n\),高度足够大的矩形网格、初始时第 \(i\) 列有 \(a_i\) 个方块。
给定参数 \(k\),你可以做不超过 \(10^4\) 次操作,来将这个网格中的所有方块全部消除,一次操作形如:
- 在网格的最顶端落下一个 \(1 \times k\) 或者 \(k \times 1\) 的方块(也就是你可以决定方块是竖着放还是横着放),直到碰到一个方块时停止下落。
- 自下而上检查所有行,如果一行被方块填满,则消除这一行的所有方块。
需要构造方案。保证 \(1 \le n, a_i \le 50\)。
首先注意到我们可以通过若干操作使得 \(a_i \gets a_i \bmod k\)。令 \(t = \lfloor \frac{\max a_i}{k} \rfloor\),通过对于每个位置 \(i\),在 \(i\) 处加入若干竖块,使得 \(a_i \in [tk, (t + 1)k)\),此时至少会消除 \(tk\) 次,于是 \(\forall i, a_i < k\)。我们称这样的操作为一次调整。
考虑 \(a\) 模 \(k\) 意义下的差分数组 \(d_{1 \sim n + 1}\),其满足 \(d_i = a_i - a_{i - 1}\),对于一种合法的终态,由于所有方块将被消空,所以 \(\forall i \in [2, n], d_i = 0\)。注意我们在 \(d_1\) 和 \(d_{n + 1}\) 处无限制。
现在从 \(d\) 的角度观察所有操作,现在加竖块 \(d\) 不变,消除一行 \(d_{2 \sim n}\) 不变,没有影响,唯一对 \(d\) 有影响的操作是在 \(i\) 处加一个横块,其影响为 \(d_i \gets d_i + 1, d_{i + k} \gets d_{i + k} - 1\),那么有解的必要条件是 \(\forall r \in [0, k), 1 \bmod k \neq r, (n + 1) \bmod k \neq r, (\sum\limits_{i \bmod k = r} d_i) \equiv 0 \pmod k\),下面我们通过构造证明其是充分的。
考虑我们一定可以通过如下操作使得 \(d_i \gets d_i + v\),\(d_{i + k} \gets d_{i + k} - v\)(\(v \in [0, k)\)):
- 在 \(i\) 处加入 \(v\) 个横块,在 \(\forall i \in [1, n] - [i, i + k)\) 处加入 \(2\) 个竖块,此时 \(v\) 个横块全部被消除,如果剩下部分存在高度大于 \(k\),即 \(a_i \ge k\) 的位置,按照前面所说的方法调整即可。
那么通过上述操作,对于 \(\bmod k = r\) 分组后 \(\sum d\) 不变,但是对于 \(1\) 和 \(n + 1\) 所在的 \(r\) 我们可以全部丢到 \(1\) 和 \(n + 1\),所以没有前面的限制。
操作次数 \(O(1) \times (n^2 + \sum a_i)\)。
Code
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;const int N = 55;int n, k;
int a[N], d[N];
vector<int> v[N];
vector<pair<int, int>> ans;void Adjust () {int mx = 0;for (int i = 1; i <= n; ++i) {mx = max(mx, a[i] / k);}for (int i = 1; i <= n; ++i) {while (a[i] < mx * k) {ans.push_back({1, i});a[i] += k; }a[i] -= mx * k;}
}void Operate (int x, int v) {if (!v) return; d[x] = (d[x] + v) % k; d[x + k] = (d[x + k] - v + k) % k;for (int i = 1; i <= v; ++i) {ans.push_back({2, x});} for (int i = 1; i <= n; ++i) {if (i < x || i >= x + k) {ans.push_back({1, i});ans.push_back({1, i});a[i] += k * 2 - v; }}Adjust();
}int main () {// freopen("tmp.in", "r", stdin);// freopen("tmp.out", "w", stdout);cin.tie(0)->sync_with_stdio(0);cin >> n >> k;for (int i = 1; i <= n; ++i) {cin >> a[i];}Adjust();for (int i = 1; i <= n + 1; ++i) {d[i] = (a[i] - a[i - 1] + k) % k;v[i % k].push_back(i);}for (int r = 0; r < k; ++r) {if (v[r].empty()) continue;int sum = 0; for (auto i : v[r]) {sum = (sum + d[i]) % k; }if (v[r][0] == 1) {for (int j = v[r].size() - 1; j; --j) {Operate(v[r][j - 1], d[v[r][j]]);}}else {if (sum && v[r].back() != n + 1) {cout << -1 << '\n';return 0; }for (int j = 0; j < v[r].size() - 1; ++j) {int i = v[r][j];Operate(i, (k - d[i]) % k);}}}int mx = *max_element(a + 1, a + n + 1);for (int i = 1; i <= n; ++i) {int cnt = (mx - a[i]) / k; for (int j = 1; j <= cnt; ++j) {ans.push_back({1, i});}}cout << ans.size() << '\n';for (auto i : ans) {cout << i.first << ' ' << i.second << '\n';}return 0;
}
T2 Selling RNA Strands
题意:给定 \(n\) 个字符串 \(s_{1 \sim n}\),有 \(m\) 次询问,每次询问格式如下:
- 给出字符串 \(p\) 和 \(q\),求 \(s_{1 \sim n}\) 中有多少个字符串同时以 \(p\) 为前缀,并以 \(q\) 为后缀。
令 \(N = \max(n, m), S = \max(\sum|s_i|, \sum|p|, \sum|q|)\),保证 \(N \le 10^5, S \le 2 \times 10^6\),字符集大小为 \(4\)。
首先考虑如果只有前缀为 \(p\) 的限制是好做的,我们对于 \(s\) 建 \(\text{Trie}\),每次查询时走到 \(p\) 对应的 Trie 上的结点,做子树标记求和即可。
现在加入后缀为 \(p\) 的限制,不难想到对 \(s\) 的反串再建一棵 \(\text{Trie}\),假设一个字符串 \(s\) 在两颗 Trie 上的对应点分别为 \(a\) 和 \(b\),某次查询的前后缀 \(p, q\) 在两颗 \(\text{Trie}\) 上的对应点分别为 \(a_0\) 和 \(b_0\),那么 \(s\) 对该询问有贡献,当且仅当 \(a_0\) 是 \(a\) 的祖先,\(b_0\) 是 \(b_0\) 的祖先。
对于祖先的限制考虑用 \(\text{dfs}\) 序刻画,那么原问题可转化成二维数点,扫描线 + 树状数组即可,时间复杂度 \(O(S + N \log S)\)。
Code
#include <iostream>
#include <algorithm>
#include <vector>
#include <numeric>using namespace std;const int N = 1e5 + 5, T = 2e6 + 5; int n, m;
int a[N], b[N], p[N], ans[N];string Read () {string s;cin >> s;for (auto &c : s)c = (c == 'A' ? 0 : (c == 'G' ? 1 : (c == 'U' ? 2 : 3)));return s;
}struct Trie {int tot;int ch[T][4], dfn[T], siz[T];int Insert (string s) {int k = 0; for (auto c : s) {if (!ch[k][c]) ch[k][c] = ++tot;k = ch[k][c];}return k; }void Dfs (int x) {dfn[x] = ++tot;siz[x] = 1; for (int i = 0, y; i < 4; ++i) {if (y = ch[x][i]) {Dfs(y);siz[x] += siz[y];}}}int Get_id (string s) {int k = 0; for (auto c : s) {k = ch[k][c];if (!k) return -1;}return k;}
} trie, rtrie;struct E {int x, l, r, v, id;
};struct Bit {int tr[T];void Add (int x, int y) {for (; x <= rtrie.tot; x += (x & -x)) {tr[x] += y;}}int Query (int l, int r) {int res = 0; for (--l; l; l -= (l & -l)) {res -= tr[l];}for (; r; r -= (r & -r)) {res += tr[r];}return res;}
} bit;int main () {cin.tie(0)->sync_with_stdio(0);cin >> n >> m;for (int i = 1; i <= n; ++i) {string s = Read();a[i] = trie.Insert(s);reverse(s.begin(), s.end());b[i] = rtrie.Insert(s);} trie.Dfs(0), rtrie.Dfs(0);for (int i = 1; i <= n; ++i) {a[i] = trie.dfn[a[i]], b[i] = rtrie.dfn[b[i]];}vector<E> v;for (int i = 1; i <= m; ++i) {string s = Read(), t = Read();reverse(t.begin(), t.end());int p = trie.Get_id(s), q = rtrie.Get_id(t);if (p != -1 && q != -1) {int al = trie.dfn[p], ar = trie.dfn[p] + trie.siz[p] - 1, bl = rtrie.dfn[q], br = rtrie.dfn[q] + rtrie.siz[q] - 1; v.push_back(E({al - 1, bl, br, -1, i}));v.push_back(E({ar, bl, br, 1, i}));}} sort(v.begin(), v.end(), [&](E a, E b) -> bool { return a.x < b.x;}); iota(p + 1, p + n + 1, 1);sort(p + 1, p + n + 1, [&](int i, int j) -> bool {return a[i] < a[j];});int t = 1; for (auto i : v) {while (t != n + 1 && a[p[t]] <= i.x) {bit.Add(b[p[t++]], 1);}ans[i.id] += bit.Query(i.l, i.r) * i.v;}for (int i = 1; i <= m; ++i) {cout << ans[i] << '\n';}return 0;
}
T3 Skyscraper
题意:给定一个长度为 \(n\) 的序列 \(a_i\),满足 \(a\) 中元素两两不相同。
给定 \(L\),计数有多少个 \(a\) 的排列 \(p\),满足 \(\sum\limits_{i = 1}^{n - 1} |p_i - p_{i + 1}| \le L\)。
\(1 \le n \le 10^2, 1 \le a_i, L \le 10^3\)。
考虑 \(\sum\limits_{i = 1}^{n - 1} |p_i - p_{i + 1}| \le L\) 的限制,显然正着是不好做的。套路的可以想到从上往下扫描线,维护连续段的数量。那么我们的要求就是线段长度总和 \(\le L\)。
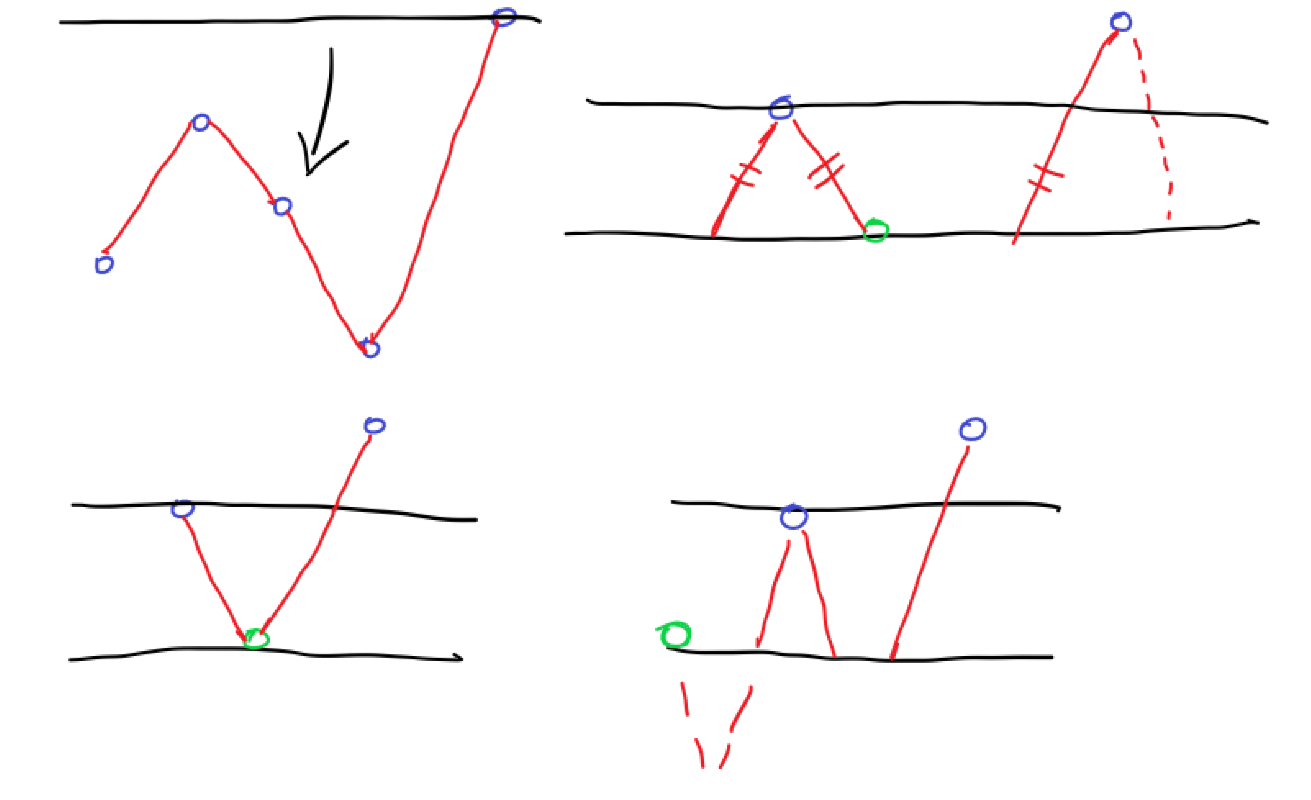
假设我们从大往小加数,假设扫描线的上一个位置为 \(lst\),当前这个数所在位置为 \(cur\),那么可能会有若干未闭合的插头,每个会对线段长度总和造成 \(lst - cur\) 的贡献。我们发现这样的插头数量至于当前的连续段数有关,于是我们并不关心当前加入的所有数的形态,而只需记录有多少个连续段。
考虑一个问题,如果一个数在边界,那么它会少贡献一个插头,如右上图所示。但是这个是好处理的,我们只需再记录位于左右边界上的数是否已经确定即可。
默认滚动数组消去当且加的是第几个数的维度。状态就是 \(f_{i, j, p, q}\),表示当前有 \(i\) 个连续段,线段总长为 \(j\),\(p, q\) 表示是否钦定了最左和最右的数的方案数。
转移有三种情况:新创建一个段、延续一个段、合并相邻的两个段,分类讨论一下即可。
时间复杂度 \(O(n^2L)\)。
Code
#include <iostream>
#include <algorithm>using namespace std;const int N = 105, M = 1e3 + 5;
const int Mod = 1e9 + 7; int n, lim;
int a[N], f[N][M][2][2], g[N][M][2][2];void Add (int &x, int y) {x = ((x += y) >= Mod ? x - Mod : x);
}int main () {cin.tie(0)->sync_with_stdio(0);cin >> n >> lim;for (int i = 1; i <= n; ++i) {cin >> a[i];}sort(a + 1, a + n + 1, greater<int>());for (int i = 0; i < 2; ++i) for (int j = 0; j < 2; ++j)f[1][0][i][j] = 1; for (int i = 1; i < n; ++i) {for (int j = 1; j <= i; ++j) {for (int k = 0; k <= lim; ++k) {for (int p = 0; p < 2; ++p) {for (int q = 0; q < 2; ++q) {g[j][k][p][q] = f[j][k][p][q], f[j][k][p][q] = 0; }}}}for (int j = 1; j <= i; ++j) {for (int k = 0; k <= lim; ++k) {for (int p = 0; p < 2; ++p) {for (int q = 0; q < 2; ++q) {int v = g[j][k][p][q];if (!v)continue;int _k = k + (j * 2 - p - q) * (a[i] - a[i + 1]);if (_k > lim) continue;Add(f[j + 1][_k][p][q], 1ll * (j - 1) * v % Mod);if (!p) {Add(f[j + 1][_k][0][q], v);Add(f[j + 1][_k][1][q], v);}if (!q) { Add(f[j + 1][_k][p][0], v);Add(f[j + 1][_k][p][1], v);}Add(f[j][_k][p][q], 2ll * (j - 1) * v % Mod);if (!p) {Add(f[j][_k][0][q], v);Add(f[j][_k][1][q], v);}if (!q) {Add(f[j][_k][p][0], v);Add(f[j][_k][p][1], v);}if (j > 1) {Add(f[j - 1][_k][p][q], 1ll * (j - 1) * v % Mod);}}}}}}int ans = 0; for (int i = 0; i <= lim; ++i) {ans = (ans + f[1][i][1][1]) % Mod;}cout << ans << '\n';return 0;
}