PDF文档公众号回复关键字:20240914

2023 CSP-S 选择题
单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项)
1 在 Linux 系统终端中,以下哪个命令用于创建一个新的目录 ? ( )
A newdir
B mkdir
C create
D mkfold
2 从0,1,2,3,4 中选取 4 个数字,能组成( )个不同四位数(注:最小的四位数是 1000 最大的四位数是 9999)
A 96
B 18
C 120
D 84
3 假设 n 是图的顶点的个数,m 是图的边的个数,为求解某一问题有下面四种不同时间复杂度的算法。对于 m=Θ(n) 的稀疏图而言,下面的四个选项,哪一项的渐近时间复杂度最小( )
A O(m* sqrt(logn) * loglogn)
B O(n^2 + m)
C O(n^2/logm + m*logn)
D O(m + nlogn)
4 假设有 n根柱子,需要按照以下规则依次放置编号为 1,2,3,⋯的圆环:每根柱子的底 部固定,顶部可以放入圆环;每次从柱子顶部放入圆环时,需要保证任何两个相邻圆环的编号之和是一个完全平方数。请计算当有 4根柱子时,最多可以放置( )个圆环
A 7
B 9
C 11
D 5
5 以下对数据结构的表述不恰当的一项是( )
A 队列是一种先进先出(FIFO)的线性结构
B 哈夫曼树的构造过程主要是为了实现图的深度优先搜索
C 散列表是一种通过散列函数将关键字映射到存储位置的数据结构
D 二叉树是一种每个结点最多有两个子结点的树结构
2 相关知识点
1) 常用linux命令
ls:列出目录中的文件和子目录。
cd:切换当前工作目录。
pwd:显示当前工作目录的路径。
cp:复制文件或目录。
mv:移动文件或目录。
rm:删除文件或目录。
mkdir:创建新目录。
rmdir:删除空目录。
touch:创建空文件或更改文件的时间戳。
cat:查看文件内容或将多个文件合并为一个文件
2) 完全平方数
完全平方数是指一个整数可以表示为另一个整数的平方的形式
1(1 * 1)
4(2 * 2)
9(3 * 3)
16(4 * 4)
25(5 * 5)
36(6 * 6)
49(7 * 7)
64(8 * 8)
81(9 * 9)
3) 稀疏图
稀疏图(Sparse Graph)是指边数相对较少的图
在稀疏图中,顶点数为n,边数为m,它们之间的一般关系是m远小于n的平方 m<nlogn
4) 队列
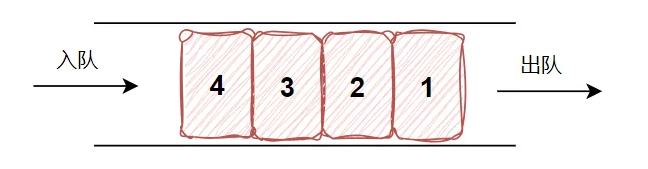
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(head)进行删除操作,而在表的后端(tail)进行插入操作
队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头
队列可以理解成我们平时的排队,先进入的先出去
5) 散列表
散列表,英文名称为Hash Table,又称哈希表、杂凑表等
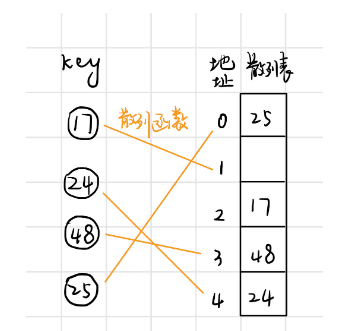
散列表是根据关键字直接访问的数据结构。散列表通过散列函数将关键字映射到存储地址,建立了关键字和存储地址之间的一种直接映射关系
例如:关键字集key = (17, 24, 48, 25),散列函数H(key) = key % 5,散列函数将关键字映射到存储地址下标,将关键字存储到散列表的对应位置
6) 二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒,例如下面是一棵二叉树
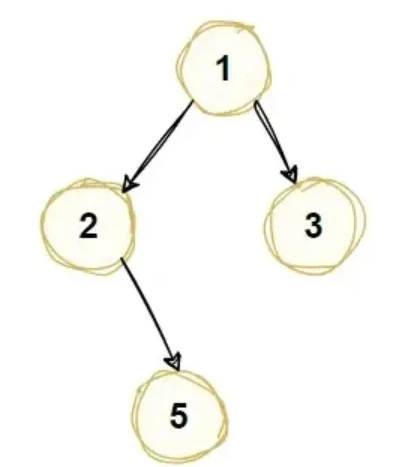
7) 哈夫曼树
1 选剩下的两棵根权值最小的树合并成一棵新树
2 新树的根权值等于两棵合并前树的根权值和
3 重复1和2
哈夫曼编码
哈夫曼树的左右孩子进行编码称为哈夫曼编码,通常左边为0,右边为1
只对叶子节点进行编码/解码,编码唯一
哈夫曼编码是前缀编码,任何一个字符的编码都不是另一个字符编码的前缀(只有叶子节点编码)
哈夫曼编码左边为0,右边为1是通常规定,也可以左边为1右边为0,但确定后编码是唯一的
如果下图为字母a,b,c,d,e的编码,字母旁边对应数字为其出现的频率
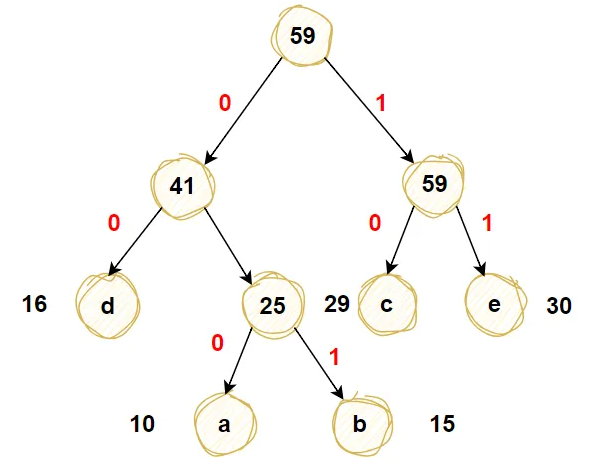
3 思路分析
1 在 Linux 系统终端中,以下哪个命令用于创建一个新的目录 ? ( B )
A newdir
B mkdir
C create
D mkfold
分析
根据常用linux命令可知,创建一个目录为mkdir
2 从0,1,2,3,4 中选取 4 个数字,能组成( A )个不同四位数(注:最小的四位数是 1000 最大的四位数是 9999)
A 96
B 18
C 120
D 84
分析
由于0不能做首位,所以不能直接使用排列
分别把这5个数字放入到4位数的对应位
千位 可以是 1 2 3 4 有4种选择
百位 可以是包括0的5个数字任意一个,千位已经使用了1个,所以有4种选择
十位 同百位,有3种选择
个位 同十位,有2种选择
根据乘法原理
4 * 4 * 3 * 2 = 96 种
3 假设 n 是图的顶点的个数,m 是图的边的个数,为求解某一问题有下面四种不同时间复杂度的算法。对于 m=Θ(n) 的稀疏图而言,下面的四个选项,哪一项的渐近时间复杂度最小( )
A O(m* sqrt(logn) * loglogn)
B O(n^2 + m)
C O(n^2/logm + m*logn)
D O(m + nlogn)
分析
根据稀疏图的定义可知,顶点远数远大于边的图
假设n=16 ,m=2时,代入4个选项
A 2 * sqrt(log16) * loglog16=2 * sqrt(4) * log4 =2 * 2 * 2=8
B 16^2+2=256+2=258
C 16^2/1 + 2 * log16=256 + 2 * 4 = 264
D 2 + 16 * log16 = 2+16*4=66
从上述计算结果看A最小,所以选 A
4 假设有 n根柱子,需要按照以下规则依次放置编号为 1,2,3,⋯的圆环:每根柱子的底 部固定,顶部可以放入圆环;每次从柱子顶部放入圆环时,需要保证任何两个相邻圆环的编号之和是一个完全平方数。请计算当有 4根柱子时,最多可以放置( C )个圆环
A 7
B 9
C 11
D 5
分析
根据题目规则每个相邻圆环的编号之和是一个完全平方数,列举几个可能的完全平方数
4,9,16,25,36
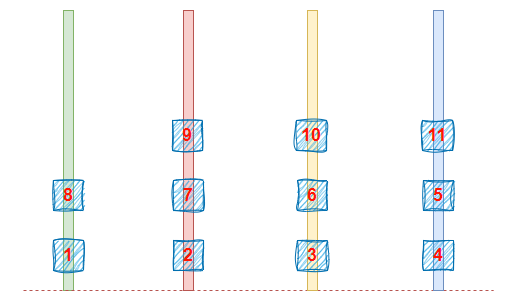
尝试依次放入圆环,可知如下情况,可以放置最多
1和8,2和7,3和6,4和5都可以组成完全平方数
再继续放
7和9,6和10,5和11都可以组成完成平方数
无法继续再放入12使得和最上面的数组成完全平方数
因此最多可以放置11个圆环
5 以下对数据结构的表述不恰当的一项是( B )
A 队列是一种先进先出(FIFO)的线性结构
B 哈夫曼树的构造过程主要是为了实现图的深度优先搜索
C 散列表是一种通过散列函数将关键字映射到存储位置的数据结构
D 二叉树是一种每个结点最多有两个子结点的树结构
分析
A 队列的特点就是先进先出,即最先进入队列的元素最先被取出,正确
B 哈夫曼树(Huffman Tree)是一种特殊的二叉树,主要用于数据压缩。它的构造过程是根据字符出现的频率来构建一棵最优二叉树,以便在数据压缩过程中实现最优编码。这与图的深度优先搜索无关,因此是错误的
C 散列表(Hash Table)是一种通过散列函数将关键字映射到存储位置的数据结构,它可以实现快速的查找、插入和删除操作,正确
D 二叉树(Binary Tree)是一种特殊的树结构,其中每个结点最多只能有两个子结点,正确
因此选B