回顾
问题陈述: 给定一棵二叉树,实现中序遍历并返回包含其中序序列的数组
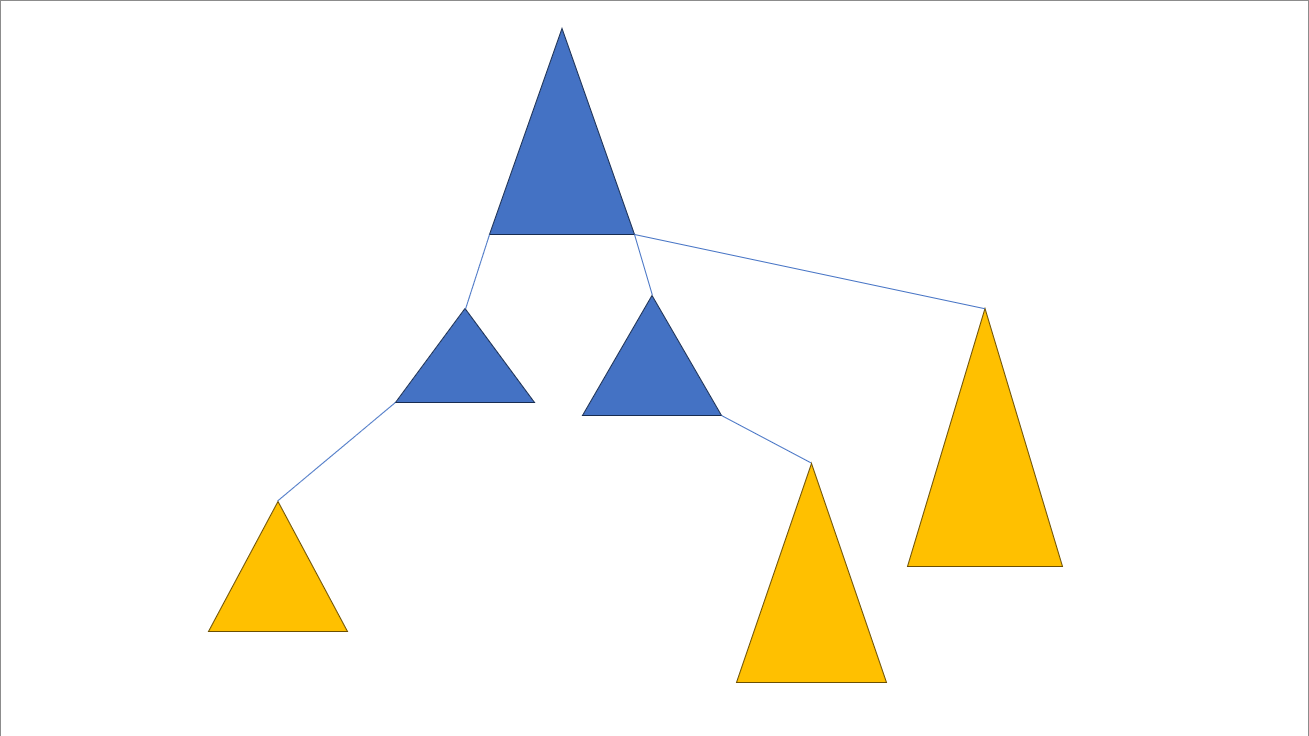
例如给定下列二叉树:
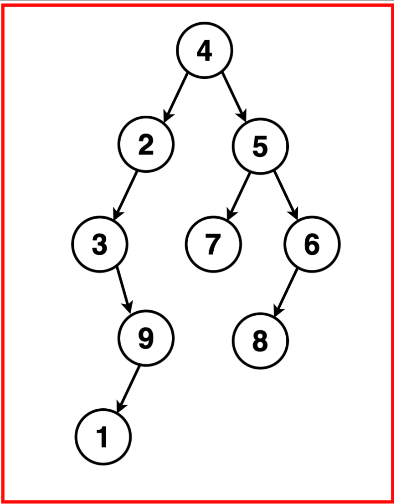
我们按照左、根、右的顺序递归遍历二叉树,得到以下遍历:
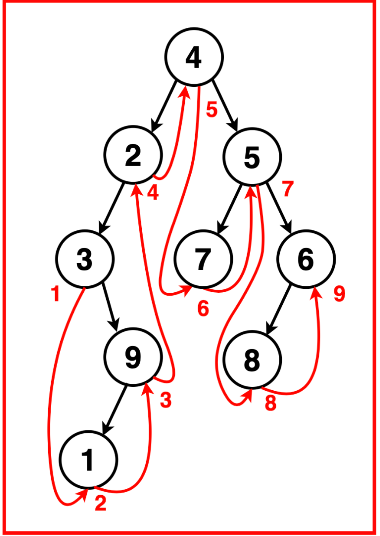
最终中序遍历结果可以输出为: [3, 1, 9, 2, 4, 7, 5, 8, 6]
Morris trick
Morris 中序遍历是一种树遍历算法,旨在实现 O(1) 的空间复杂度,无需递归或外部数据结构。该算法应高效地按中序顺序访问二叉树中的每个节点,并在遍历过程中打印或处理节点值,而无需使用堆栈或递归。
点击查看代码
#include <iostream>
#include <sstream>
#include <unordered_map>
#include <vector>
#include <queue>
#include <map>using namespace std;// TreeNode structure
struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};class Solution {
public:// Function to perform iterative Morris// inorder traversal of a binary treevector<int> getInorder(TreeNode* root) {// Vector to store the// inorder traversal resultvector<int> inorder;// Pointer to the current node,// starting from the rootTreeNode* cur = root;// Loop until the current// node is not NULLwhile (cur != NULL) {// If the current node's// left child is NULLif (cur->left == NULL) {// Add the value of the current// node to the inorder vectorinorder.push_back(cur->val);// Move to the right childcur = cur->right;} else {// If the left child is not NULL,// find the predecessor (rightmost node// in the left subtree)TreeNode* prev = cur->left;while (prev->right && prev->right != cur) {prev = prev->right;}// If the predecessor's right child// is NULL, establish a temporary link// and move to the left childif (prev->right == NULL) {prev->right = cur;cur = cur->left;} else {// If the predecessor's right child// is already linked, remove the link,// add current node to inorder vector,// and move to the right childprev->right = NULL;inorder.push_back(cur->val);cur = cur->right;}}}// Return the inorder// traversal resultreturn inorder;}
};int main() {TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->left->left = new TreeNode(4);root->left->right = new TreeNode(5);root->left->right->right = new TreeNode(6);Solution sol;vector<int> inorder = sol.getInorder(root);cout << "Binary Tree Morris Inorder Traversal: ";for(int i = 0; i< inorder.size(); i++){cout << inorder[i] << " ";}cout << endl;return 0;
}