T2 树上异或
题面
分析
树形 DP 题
考虑一颗子树内部的某种割边方式,假设其被分为 \(n\) 个连通块,每个连通块的权值分别为 \(a_1, a_2, \dots, a_n\),那么该子树在这种割边方式下对答案的贡献就为 \(\prod_{i = 1}^{n} a_i\)。
因此就可以从叶子向根不断合并,求出每种割边状态的值,时间复杂度为 \(O(2^{n - 1}n)\),期望得分 \(8\) 分。
这启示往树形 DP 的方向思考。
将每次定下割边的方法转变,考虑在 DP 过程中通过将两个连通块连接到一起,去遍历每一种状态。
这样,每回溯到一个点:
- 遍历该点的子树
- 把与该点之间存在割边的连通块与该点之前所找到的连通块合并
- 每次合并后求出该情况的贡献(如图,将蓝色连通块的权值异或在一起,然后计算结果)
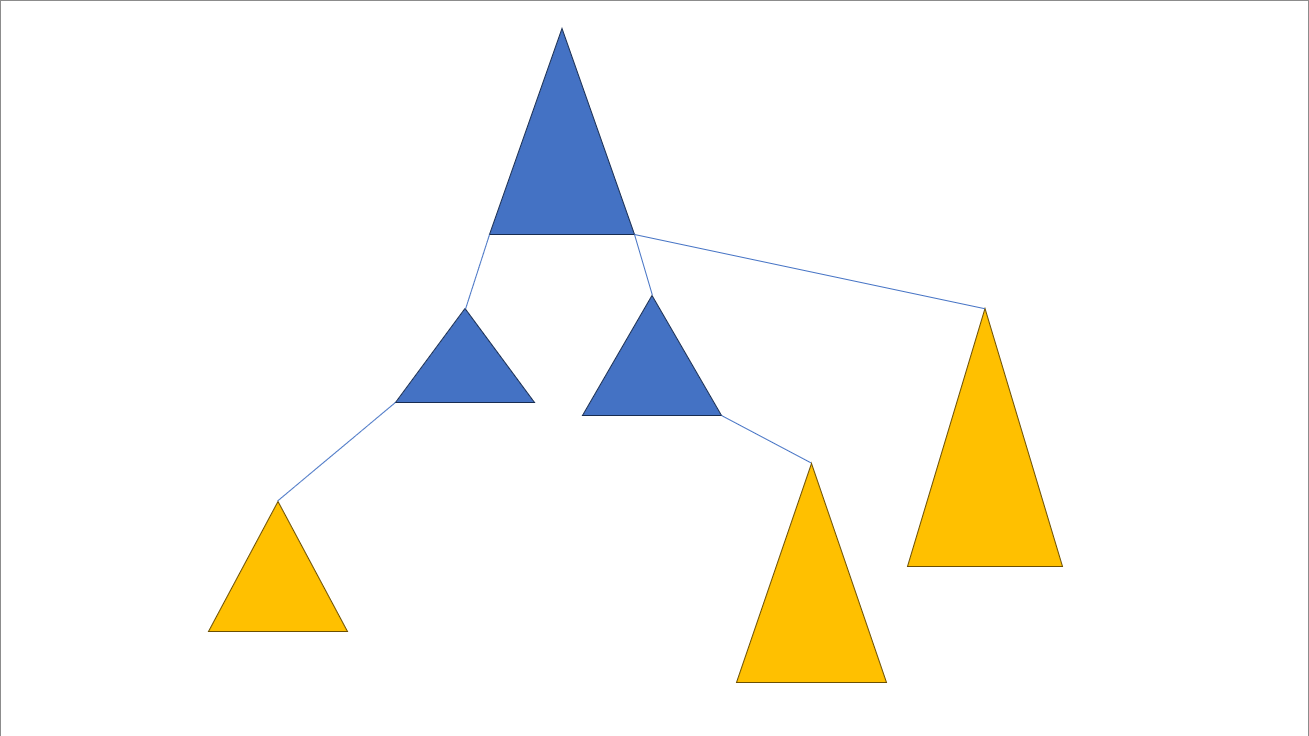
实现困难,时间复杂度极高。
因为连通块对答案的贡献是 \(\prod_{i = 1} ^{n} a_i\) 的形式,故某子树除去被合并的连通块后不同情况产生的贡献是可以累加的。(答案是 \(a_1 b_1+\dots+a_1 b_n+a_2 b_1+\dots+a_n b_n\),即 \((a_1+\dots+a_n)(b_1+\dots+b_n)\))。
而合并连通块却无法这样优化。
对此,有一种方法能够快速地合并连通块——拆位。
具体来说,定义 \(f_{u, i, j}\) 表示以 \(u\) 所在的连通块的权值第 \(i\) 位为 \(j\) 时以 \(u\) 为根节点的子树除了\(u\) 所在的连通块其他连通块的乘积的值,定义 \(g_u\) 表示以 \(u\) 为根节点的子树对答案的贡献。
容易得到:$$g_u = \sum_{i = 0}^{63}f_{u, i, 1} \times 2^i$$,即 \(u\) 所在连通块第 \(i\) 位为 \(1\) 时,所有的割边方案的贡献。
故仅需考虑 \(f_{u, i, j}\) 的转移。
考虑当前遍历到 \(u\) 的儿子节点 \(v\),则:
- 如果不合并,则 \(v\) 的子树全都与 \(u\) 所在的连通块无关,那么 \(g_v\) 全都要乘到 \(f_{u, i, 0}\)。
- 合并第 \(i\) 位为 \(1\) 的情况,如果连通块原本为 \(1\) ,则与该子树中第 \(i\) 位为 \(0\) 的异或后第 \(i\) 位仍然为 \(1\)。否则为与第 \(i\) 位为 \(1\) 的连通块异或。
- 第 \(i\) 位为 \(0\) 则恰好相反。
即:
答案为 \(g_1\)。
注意
本题空间较小,动态规划数组开 long long 会爆。
/*--------------------------------| code by FRZ_29 || code time || 2024/09/15 || 13:42:20 || 星期天 |--------------------------------*/#include <iostream>
#include <climits>
#include <cstdio>
#include <ctime>
typedef long long LL;using namespace std;void RD() {}
template<typename T, typename... U> void RD(T &x, U&... arg) {x = 0; int f = 1;char ch = getchar();while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }while (ch >= '0' && ch <= '9') x = (x << 3) + (x << 1) + ch - '0', ch = getchar();x *= f; RD(arg...);
}const int N = 5e5 + 5;
const int mod = 998244353;#define PRINT(x) cout << #x << "=" << x << "\n"
#define LF(i, __l, __r) for (int i = __l; i <= __r; i++)
#define RF(i, __r, __l) for (int i = __r; i >= __l; i--)int head[N], Next[N << 1], ver[N << 1], tot = 1;
int n, f[N][65][2], g[N];
LL a[N];void add(int u, int v) {ver[++tot] = v;Next[tot] = head[u], head[u] = tot;
}void dfs(int u, int _f) {LF(i, 0, 63) f[u][i][a[u] >> i & 1] = 1;for (int i = head[u]; i; i = Next[i]) {int v = ver[i];if (v == _f) continue;dfs(v, u);LF(i, 0, 63) {LL t0 = f[u][i][0], t1 = f[u][i][1];f[u][i][0] = (t0 * g[v] + t0 * f[v][i][0] + t1 * f[v][i][1]) % mod;f[u][i][1] = (t1 * g[v] + t1 * f[v][i][0] + t0 * f[v][i][1]) % mod;}}LF(i, 0, 63) g[u] = (g[u] + (1LL << i) % mod * f[u][i][1]) % mod;
}int main() {
// freopen("read.in", "r", stdin);
// freopen("out.out", "w", stdout);
// time_t st = clock();RD(n);LF(i, 1, n) RD(a[i]);LF(u, 2, n) {int v; RD(v);add(u, v), add(v, u);}dfs(1, 0);printf("%d", g[1]);
// printf("\n%dms", clock() - st);return 0;
}/* ps:FRZ弱爆了 */