数学知识（初赛）

求最大公约数的技巧

---

 

利用辗转相除法，gcd（A，B）=gcd（B，A%B），就可以很快速求解。

应用：化简分数，数学题等等。

 

原理：理解为一个长方形，然后要尽量去铺最大正方形，以满足铺满长方形。最后一个铺满长方形的那个正方形肯定是最大公约数。

如下图，这个长方形先铺一个绿色正方形，再在剩下的空余地方铺红色，这样以此类推，最后铺到紫色刚好铺满。所以ans=紫色边长

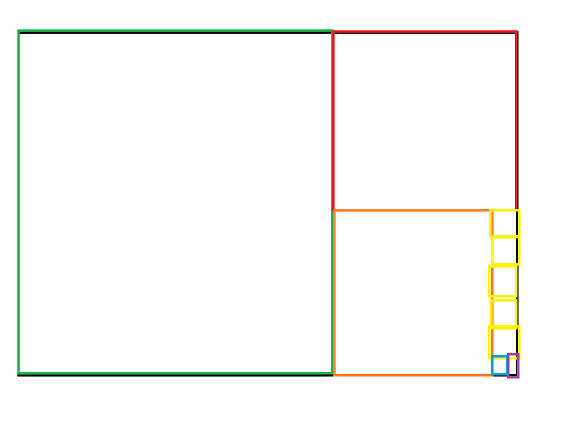
 比较抽象，建议看网上的。

 

 

快速判质数

---

 

首先判2,3,5

然后判7,11,13

一个数假设n位，（前（n-3）位   -   后三位）%（7或11或13）=0，就可以被整除

 

例如：5895942，5895-942=4953，4953/13余0，这个数可以被13整除

 

证明：例如ABCDEF

ABCDEF   =   ABC000+DEF+ABC-ABC   =   ABCABC+DEF-ABC   =   A*100000+B*10000+C*1000+A*100+B*10+C+DEF-ABC   =   A*100100+B*10010+C*1001+DEF-ABC   =   1001(A*100+B*10+C）+DEF-ABC

注意到1001能被7,3,13整除，所以只需要看最后面的DEF-ABC能否被整除即可。