题目描述
给定一根 \(1\) 到 \(N\) 的数轴。一开始有一个棋子在 \(N\)。每次棋子 \(x\) 可以跳到 \(x-1,x+1\) 或 \(x\) 的因子处(不能超出 \(1\) 到 \(N\))。
每个点只能到达一次。求棋子到达 \(1\) 的方案数。
思路
由于求倍数比因子简单,所以把问题变成从 \(1\) 到 \(N\),每次跳倍数。
我们可以发现,棋子的行走路径由两种类型的路拼在一起:
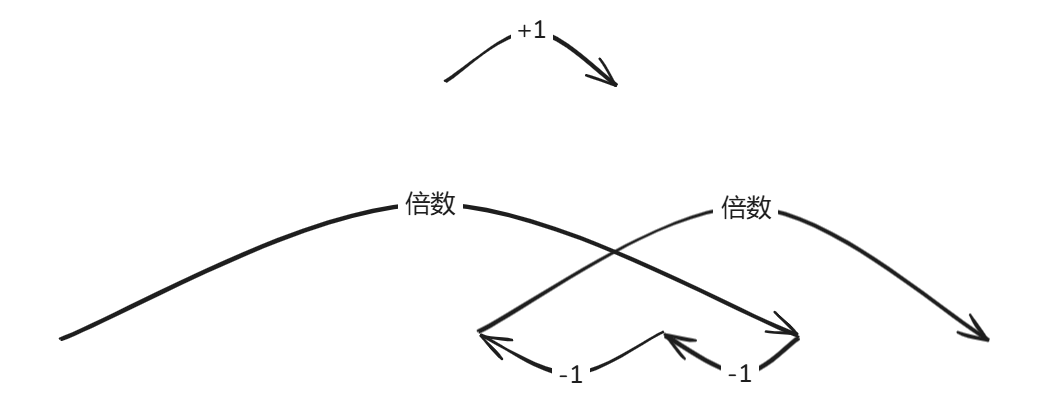
由于有先跳倍数再 \(-1\) 的跳法,此时跳的倍数必须大于走过的最远的位置,所以状态中要记录最远走到哪里。
令 \(dp_{i,j}\) 表示当前在 \(i\),最远走到了 \(j\) 的方案数。
当 \(i=j\) 时,我们有转移 \(dp_{i+1,i+1}\leftarrow dp_{i,j}\)。
当然我们也可以跳倍数,也就是对于每个 \(k=i\cdot m(m>1)\),那么都有转移 \(dp_{x,k}\leftarrow dp_{i,j}(j<x\le k)\)。
而这种转移可以使用前缀和维护。
空间复杂度 \(O(N^2)\),时间复杂度 \(O(N^2\log N)\)。
代码
#include<bits/stdc++.h>
using namespace std;const int MAXN = 5005;int n, MOD, dp[MAXN][MAXN], sum[MAXN][MAXN];int main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);cin >> n >> MOD;dp[1][1] = 1;for(int i = 1; i <= n; ++i) {for(int j = i; j <= n; ++j) {sum[j][i] = sum[j][i] + sum[j][i - 1] - (sum[j][i] + sum[j][i - 1] >= MOD ? MOD : 0);//cout << sum[j][i] << " \n"[j == n];dp[i][j] = dp[i][j] + sum[j][i] - (dp[i][j] + sum[j][i] >= MOD ? MOD : 0);//cout << dp[i][j] << " \n"[j == n];if(i == j) {dp[i + 1][max(i + 1, j)] = dp[i + 1][max(i + 1, j)] + dp[i][j] - (dp[i + 1][max(i + 1, j)] + dp[i][j] >= MOD ? MOD : 0);}for(int k = 2 * i; k <= n; k += i) {if(k > j) {sum[k][j + 1] = sum[k][j + 1] + dp[i][j] - (sum[k][j + 1] + dp[i][j] >= MOD ? MOD : 0);}}}}cout << dp[n][n];return 0;
}