\(\text{Tarjan}\)
1.引入概念
1.强连通分量
1.定义
在有向图 \(G\) 中,强连通分量就是满足以下条件的 \(G\) 的子图:
- 从任意一点出发,都有到达另一个点的路径。
- 不存在一个或者几个点,使得这个子图加入这些点后,这个子图还满足上一个性质。
为什么要限定”在有向图中“而不是”在任何一个图中“?这是因为在无向图中,只要图连通,那么任意一点都有到另外一点的路径,可以用并查集维护,这个时候 \(\text{Tarjan}\) 就没有存在的必要了。
当然,后面 \(\text{Tarjan}\) 会有在无向图中的用处。
2.性质
我们想一想,一个强连通分量中,既然每一个点都有到达另外一个点的路径,那么对于这个强连通分量中的任意一条边 \(u\rightarrow v\) 的两个端点来说,都存在 \(v\) 到 \(u\) 的路径,那么这个强连通分量一定在一个”大环“上。
当然了,这个”大环”不是严格意义上的环,它可以经过重复的点,就像这样:
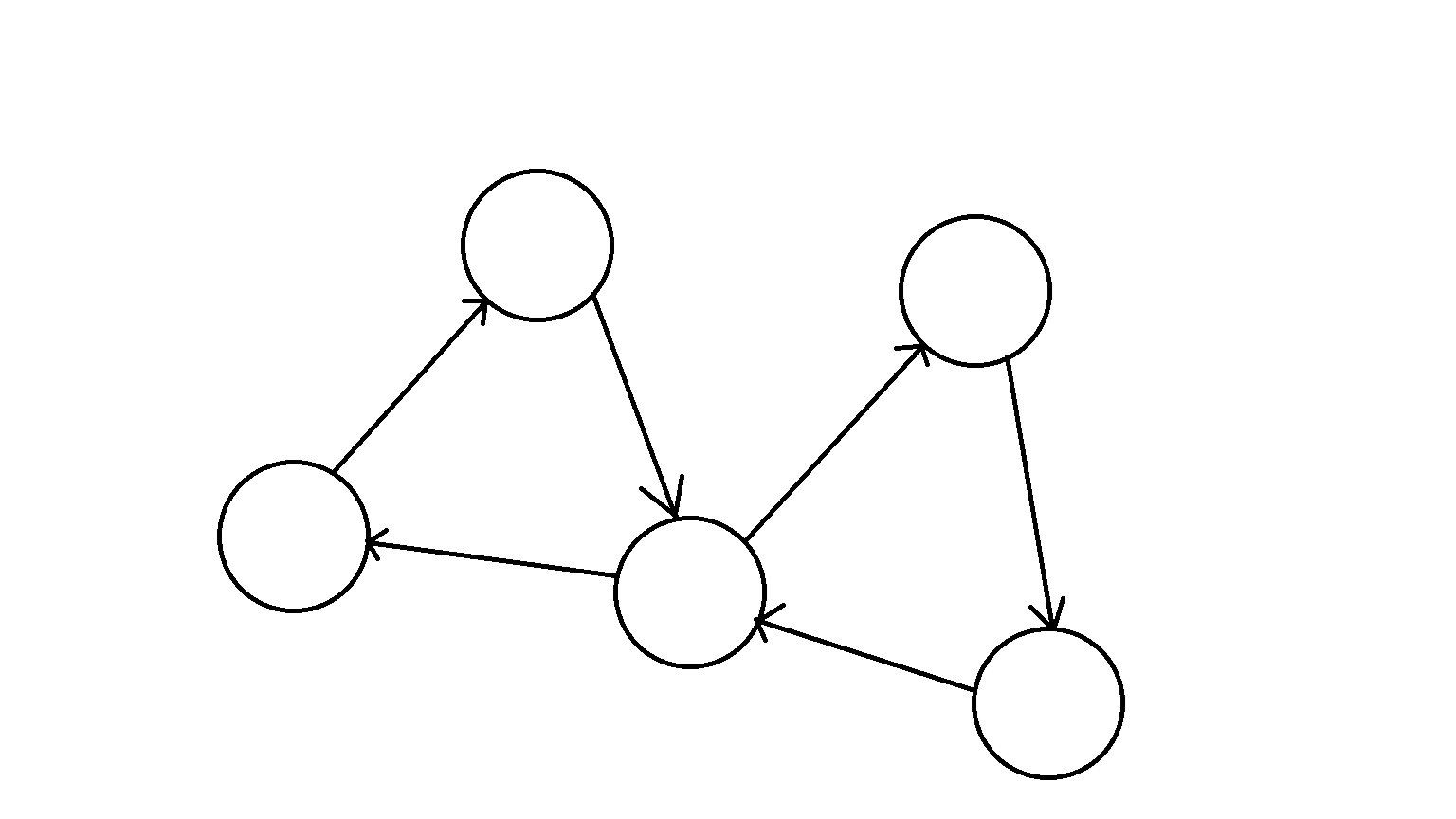
这个图告诉了我们什么?一个强连通分量要么是一个大环,要么是由几个有交点的小环组成的。
后面的讲解中,我们会反复提到“大环”,请注意这个概念。“大环”表示一个子图中,从任意一个点出发,不重不漏地经过每条边一次,最后能够回到这个点。“大环”和强连通分量、环的关系是这样的:环 \(\subsetneq\) “大环”,“大环” \(\subsetneq\) 强连通分量。
2.时间戳
1.定义
按照 \(\text{DFS}\) 遍历的过程,以每个结点第一次被访问时的顺序,依次给 \(n\) 个结点标上 \(1\sim n\) 的标记,那么这个标记就叫做时间戳,记作 \(dfn\)。
2.作用
这个在讲 \(\text{Tarjan}\) 的缩点算法逻辑的时候会讲到。
3.边的分类
1.深度优先树的定义
我们在执行 \(\text{DFS}\) 算法的时候,会经过 \(n-1\) 条边和所有 \(n\) 个点,这些边和点会构成一棵树,叫做深度优先树。
就比如下面这个图,它的深度优先树就是红色边:
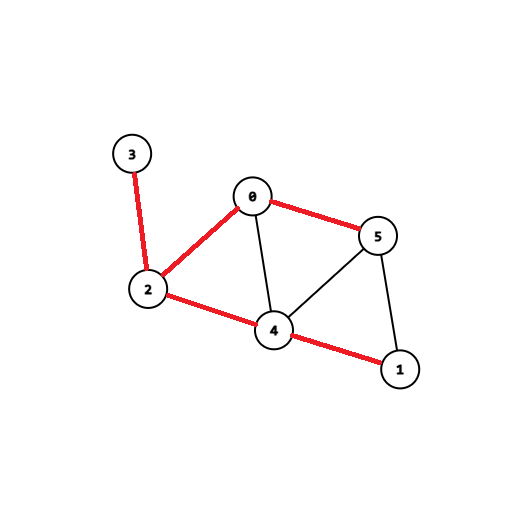
这里说明一个事情:本篇中所有形如 “\(u\) 的子树”的描述,都包括 \(u\) 本身,除非特殊说明。以及,所有形如“\(u\) 的祖先”的描述,都包括 \(u\) 本身,除非特殊说明。
2.边的分类
树边:指深度优先树中的边。
后向边:在一棵深度优先树中,从一个点 \(u\) 出发,连接到其祖先 \(anc\) 的边,这里可能有 \(anc=u\)。
前向边:在一棵深度优先树中,从一个点 \(u\) 出发,连接到其子树中一个点 \(v\) 的边,这里不可能有 \(v=u\)。
横叉边:指其它所有的边。
4.割点、点双连通、割边、边双连通
1.定义
在一个图 \(G\) 中:
割点:删去一个点 \(u\) 及所有与 \(u\) 相关的边,图就不连通了,那么 \(u\) 称为 \(G\) 的割点。
点双连通:图中没有割点,就说 \(G\) 是点双连通的。
割边:删去一条边 \(e\) 后,图就不连通了,那么称 \(e\) 为 \(G\) 的割边。
边双连通:图中没有割边,就说 \(G\) 是边双连通的。
2.性质
割点、割边都是无向图中的概念。
一个图的割点不止一个,这就是 \(\text{Tarjan}\) 算法存在于无向图中的意义。
如果一条边 \(e=u\rightarrow v\) 是割边,那么 \(u\) 和 \(v\) 是割点。
2.\(\text{Tarjan}\) 的缩点算法逻辑
1.定义
\(\text{Tarjan}\) 的经典用处就是拿来缩点。
首先,我们需要了解为什么要缩点。在一个强连通分量中,每个点都可以互相到达,那么这个强连通分量就可以缩成一个点,每个强连通分量的子问题内部处理。这就是缩点的原因。
2.不同类型的边在强连通分量中的作用
树边:以下的讨论都是基于树边展开的。
后向边:十分有用。一条后向边 \(u\rightarrow anc\) 可以和深度优先树上 \(anc\) 到 \(u\) 的路径形成一个环,而环上每个点都是可以互相到达的。
前向边:没啥用。因为其不能构成环,对缩点没有帮助。
横叉边:部分有用。对于一条横叉边 \(u\rightarrow v\) 而言,如果有一条路径,从 \(v\) 出发,到达一个点 \(anc\),而这个 \(anc\) 又恰好是 \(u\) 的祖先结点,那么 \(u\rightarrow v\) 这条边就在一个环上了。
3.主算法逻辑
看了上面,你应该就知道 \(\text{Tarjan}\) 要干嘛了。它的作用,就是对于每一个点 \(u\),找到与 \(u\) 能够构成”大环“的所有结点。
那么怎么找?前面说过,”大环“只能由三种边构成,树边、后向边和横叉边。为了找到通过“后向边”和“横叉边”构成的环,\(\text{Tarjan}\) 算法在 \(\text{DFS}\) 的过程中维护了一个栈。
当访问到某一个点 \(u\) 的时候,栈中需要保留以下两类结点:
- 深度优先树上 \(u\) 的祖先结点。这是为了维护后向边。
- 已经访问过,且存在一条路径到达 \(u\) 的祖先结点的结点。这是为了维护横叉边。
一句话概括,就是能够到达 \(u\) 且已经访问过的结点。
我们想想,对于一个在栈中的点 \(t\),什么情况下,\(u\) 和 \(t\) 才会同在一个”大环“上?一定要有一条 \(u\rightarrow t\) 的边才行吗?不是的,只要有一条 \(u\rightarrow t\) 的路径就可以了。什么时候才会有一条 \(u\rightarrow t\) 的路径?
对于所有从 \(u\) 出发的边 \(u\rightarrow v\),有两种情况:
- \(v\) 没有被访问过。这说明 \(v\) 在 \(u\) 的子树中,\(u\rightarrow v\) 这条边是树边。只要 \(v\) 的子树中有一条边连向 \(t\),说明 \(u,v,t\) 在一个“大环”上。
- \(v\) 被访问过。如果 \(v\) 不在栈中,那么这条边并没有什么用处;否则 \(u,v,t\) 在一个“大环”上。
问题似乎已经解决了,不是吗?我们知道什么情况下 \(u,v,t\) 在一个大环上。那这要怎么写进代码呢?
注意,我们的思路已经完成,下面的一切定义和概念,都不是思路里面本身就存在的,只是为了实现代码方便。
我们定义一个追溯值 \(low\),那么对于一个结点 \(u\),其追溯值 \(low_u\) 定义为满足以下条件结点 \(v\) 的最小时间戳:
- \(v\) 在栈中。
- 存在一条从 \(u\) 的子树出发的边,以 \(v\) 为终点。
接下来就彻底到代码部分了。
4.代码逻辑
首先,日常敲一个空壳。
void Tarjan(int u){}
接下来,我们既然已经访问到 \(u\) 这个结点了,当然要把 \(u\) 入栈,并且初始化 \(u\) 的 \(dfn\) 和 \(low\)。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中
}
初始化完了,我们应该进入到主算法部分。回头再看看主算法逻辑,你会发现主算法的核心就是扫描每一条边,后面的任何处理都只跟边有关。我用的是 \(\texttt{vector}\) 存图,看不惯的同学可以看注释了解一下什么意思。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中for(int v:g[u]){//扫描每一条从u出发到v结束的边}
}
我们的主算法逻辑中,边是不是分两种?我们先来讨论第一种,也就是 \(v\) 没有被访问过的情况。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中for(int v:g[u]){//扫描每一条从u出发到v结束的边if(!dfn[v]){//v还没有被访问过Tarjan(v);//扫描v的子树}}
}
扫描完了 \(v\) 的子树,总不能对 \(u\) 啥都不干吧?我们想想 \(low\) 值此时该怎么更新。
由于 \(v\) 的子树一定是 \(u\) 的子树,所以 \(low_u=\min(low_u,low_v)\)。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中for(int v:g[u]){//扫描每一条从u出发到v结束的边if(!dfn[v]){//v还没有被访问过Tarjan(v);//扫描v的子树low[u]=min(low[u],low[v]);//更新u的low值}}
}
那么我们现在来讨论第二种情况,也就是 \(v\) 被访问且 \(v\) 在栈中。这种情况下,这个结点 \(v\) 满足“存在一条从 \(u\) 出发的边,以 \(v\) 为终点”,所以更新。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中for(int v:g[u]){//扫描每一条从u出发到v结束的边if(!dfn[v]){//v还没有被访问过Tarjan(v);//扫描v的子树low[u]=min(low[u],low[v]);//更新u的low值}else if(vis[v]){//v被访问过且在栈中low[u]=min(low[u],dfn[v]);//更新u的low值}}
}
这个时候“是否在一个强连通分量中”已经判完了,但是我们总是要用一个点来代表一个强连通分量的呀,并不是每个点都有资格代表一个强连通分量的。
注意到之前没有自主的出栈操作,也就是说,else if(vis[v])这一块可能存在前向、后向、横叉三种边。
对于前向边 \(u\rightarrow v\),\(dfn_v>dfn_u\) 恒成立,所以 \(low_u\) 不会更新。
对于后向边 \(u\rightarrow v\),\(dfn_v<dfn_u\) 恒成立,所以 \(low_u\) 可能更新。
对于横叉边 \(u\rightarrow v\),由于“\(v\) 被访问过且在栈中”,所以 \(v\) 比 \(u\) 先访问,所以 \(dfn_v<dfn_u\) 恒成立,\(low_u\) 可能更新。
我们要找到一个点“能够代表一个强连通分量”,这个点应该满足什么性质?当然是以它出发的边中,既无横叉边,又无后向边。这样的点在每一个强连通分量中只有一个,所以具有代表性。
下证为什么这样的点在每一个强连通分量中只有一个,懂得的同学可以不看。
很简单,如果有两个,以其中一个为祖先开始沿深度优先树 \(\text{DFS}\) 遍历,另一个点是连不回来的,没有向回的路径,也就是说这两个点不是能互相到达的。与“强连通分量”矛盾,舍。
这里就体现了 \(low\) 数组的作用了。什么情况下,以一个点 \(u\) 出发的边中,既无横叉边,又无后向边?只有 \(low_u=dfn_u\) 的时候。
在栈中,这个点 \(u\) 到栈顶的所有点都能构成一个“强连通分量”。也就是说,当且仅当 \(dfn_u=low_u\) 的时候,我们才把 \(u\) 以上的所有点出栈,使它们构成一个强连通分量。
为什么这样是对的?因为栈中从 \(u\) 到栈顶所有点,除 \(u\) 以外,都是有横叉边或者后向边的。也正因为如此,它们才会被压在栈中。
现在 \(u\) 出现了,它可以代表一个强连通分量,于是栈中所有点都找到了自己的“归属”。
于是,至此 \(\text{Tarjan}\) 缩点功德圆满。
void Tarjan(int u){low[u]=dfn[u]=++tim;//tim表示访问到的时间stk[++tp]=u;//用数组模拟栈vis[u]=true;//vis[u]表示u是否在栈中for(int v:g[u]){//扫描每一条从u出发到v结束的边if(!dfn[v]){//v还没有被访问过Tarjan(v);//扫描v的子树low[u]=min(low[u],low[v]);//更新u的low值}else if(vis[v]){//v被访问过且在栈中low[u]=min(low[u],dfn[v]);//更新u的low值}}if(dfn[u]==low[u]){//能够代表一个强连通分量的点int v;++scc_cnt;//增加一个强连通分量do{v=stk[tp--];//出栈vis[v]=false;//不再在栈中scc[v]=scc_cnt;//v所属的最大强连通分量是scc_cnt}while(u!=v);}
}
给道例题
3.\(\text{Tarjan}\) 的割点割边算法逻辑
1.定义
首先,我们要明白,这一类问题是多种多样的,而我们要用一个算法全部解决。
这类问题可不是简简单单判个双连通就能够结束的。图中有多少个割点?多少条割边?删去割点最多剩下多少连通块?
2.主算法逻辑
首先我们来说割点。
割点算法的起步当然是判定割点。我们还是以深度优先树为基,讨论:什么情况下一个点才是割点?
考虑割点定义。如果把某个点 \(u\) 删除,图不连通,那么 \(u\) 就是割点。在深度优先树上,这条性质表现为:在 \(u\) 的儿子集合 \(son_u\) 中,如果存在一个点 \(v\in son_u\),使得 \(v\) 的子树中没有点能够到达 \(u\) 的祖先(不包括 \(u\)),那么自然而然 \(u\) 就是一个割点。
欸,但是有一个特例。如果 \(u\) 本身就是深度优先树的根节点,那一定没有点可以到达 \(u\) 的祖先(不包括 \(u\)),是不是 \(u\) 一定是割点呢?不是的。如果 \(u\) 只有一个子树,那么 \(u\) 不是割点;如果 \(u\) 有两个以上的子树,说明 \(u\) 就一定是割点了。
那要怎么写进代码呢?上一次我说这句话的时候,引出了追溯值 \(low\),这次也不会例外。
我们定义一个追溯值 \(low\),那么对于一个结点 \(u\),它的追溯值 \(low_u\) 就表示其子树中所有结点能够抵达的时间戳最小的结点。
我们想想,是不是当 \(dfn_u\le low_v(v\in son_u)\) 的时候,就说明 \(u\) 是一个割点了?因为没有方式能够从 \(v\) 的子树到达 \(u\) 的祖先(后向边)或者离开 \(u\) 的子树通向外界(横叉边)。这里 \(u\) 的祖先不包括 \(u\)。
为什么 \(dfn_u=low_v\) 时 \(u\) 依然是割点呢?因为 \(u\) 删去后,和 \(u\) 所有相关的边都会删去,就算能够到达 \(u\) 也没关系。
那么割点就这样愉快地判完了,比缩点简单得多。
割边与割点的判定十分相似,甚至一模一样。如果没有方式能够从 \(v\) 的子树到达 \(u\) 的祖先(后向边)或者离开 \(u\) 的子树通向外界(横叉边),说明 \(e=u\rightarrow v\) 就是一条割边了。\(u\) 的子树不包括 \(u\)。
我们观察到这里实际上和割点判定只有一个条件不一样,也就是“\(u\) 的子树不包括 \(u\)”。那么,在割点中,就算 \(dfn_u=low_v\), \(u\) 依然是割点,原因已经解释。但是,在割边中,\(dfn_u=low_v\) 的时候,\(e\) 就不是一条割边了,因为 \(u\) 并不会随 \(e\) 的删去而删去,\(v\) 子树中的结点仍然可以到达 \(u\)。所以,割边的判定条件是:\(dfn_u<low_v\)。
3.代码
这割点割边可比缩点好写多了,也好理解多了……
在这里只放一个割点的代码:
void Tarjan(int u){dfn[u]=low[u]=++tim;//初次访问int cnt=0;//砍掉u后图分裂成cnt连通块for(int v:g[u]){//扫描u的每一个儿子vif(!dfn[v]){Tarjan(v);//扫描v子树low[u]=min(low[v],low[u]);//更新low值if(dfn[u]<=low[v]){++cnt;}}else{low[u]=min(low[u],dfn[v]);//更新u子树中能够到达的结点dfn最小值}}if(u!=anc){++cnt;}if(cnt>=2){iscut[u]=true;//其是割点}
}

![洛谷P5683 [CSP-J2019 江西] 道路拆除](https://img2024.cnblogs.com/blog/3503483/202409/3503483-20240922160054546-126928666.png)