引言
多智能体系统协同控制算法起源于计算机领域关于分布式计算的研究,后由于数学家们的强势加盟,控制领域的研究一度占领高地。随着人工智能的发展,以多智能体强化学习为代表作的计算机领域专家又重回巅峰。
目前,每年多智能体相关的论文的都浩如烟海,成就了一批手持屠龙宝刀的研究生/教授,其中大部分苦于无龙可屠或宝刀生锈。
尽管如此,总有新人前仆后继,因此想把多智能体协同控制算法的基础知识整理一下,方便后学者入门,然后评估自己是否真心喜欢或适合。
是,则加倍努力学习更深层次的理论,以“将理论落地”为学习目标,切实地去影响物理世界。
否,则尽快在现有文献上小修小补,达到毕业要求后,做自己真正喜欢的内容。
参考文献:[1] Frank L. Lewis, Hongwei Zhang, et al. Cooperative Control of Multi-Agent Systems – Optimal and Adaptive Design Approaches[M]. 2014.(系列文章的主要内容翻译自这本书,后续不再特意说明)
[2] Wei Ren, Randal W. Beard. Distributed consensus in Multi-vehicle Cooperative Control[M]. 2008.
[3] Qu ZhiHua. Cooperative Control of Dynamical Systems: Applications to Autonomous Vehicles[M]. 2009.
适宜读者:需要研究相关内容的研究生、工程师。读者需熟悉高等数学、线性代数、现代控制理论及matlab的基础知识。
系列内容:①代数图论,连续/离散一阶(高阶)多智能体的一致性理论;②连续时间系统一致性算法的Riccati设计方法;③离散时间系统一致性算法的Riccati设计方法。
预期目标:阅读完系列文章后,读者应该①熟练掌握基本的多智能一致性算法,并能通过matlab进行仿真验证;②具备基本的文献阅读能力,愿意尝试推导Automatica 期刊上的相关论文,不至于发怵;③(工程师)能够将一致性算法应用到实际工程中,对理论算法进行实验验证。
需要说明,计算机领域的多智能体强化学习和控制领域的多智能体协同/一致性差异是很大的,这个系列主要是从控制领域进行叙述。
自麦克斯韦的《论调速器》开始,控制理论从只能处理单输入单输出(Single Input Single Output,SISO)系统,发展成熟为可以应对复杂的多输入多输出(Multiple Input Multiple Output,MIMO)系统。
典型的单输入单输出(SISO)系统:个体烧热水(温度控制系统),输入为“加热”,输出为“水温”。
典型的多输入多输出(MIMO)系统:群体烧热水(北方的集中供暖),输入为“加热+水泵”,输出为“水温+水流速度”。
烧热水是个技术活。对于简单的温控系统(SISO),整个系统只有一个单片机(控制器),一个“热得快”(执行器)。
而北方的集中供暖由于地理范围很大,可以根据不同的区域进行分区,每个片区都可以看做是一个简单的执行器。另外有一个控制中心,所有的信息都采集并上传至控制中心,控制中心经过计算,下发控制命令到每一个执行器,从而实现预期控制功能:烧热水。
这两种烧热水方式只是规模大小不同,本质都可以看做是集中式控制:仅有一个控制中心,有一个或多个执行器。
当系统的规模比较小时,集中式控制方案是一种高效的解决方式。
随着系统规模的增大,集中式方案将捉襟见肘。例如需要一台计算机控制整个东北三省所有的供暖设施时,得找计算能力多强大的计算机才能实时地完成这个任务?
事实上,每个片区不愿意只当木头人(执行器),也想有灵魂(控制器)。于是可采取分而治之方法,每个片区都安装一个单片机控制的供暖设施(赋予灵魂)。这种控制方法,可称为分散式控制。
集中式控制方案的缺点在于:①需要强大的控制中心;②成本(时间成本和经济成本)随着系统规模的线性增加而指数型增加;③当控制中心出问题时,所有人都得挨冻。
分散式控制方案的优点在于:①常规商用的控制器即可实现控制目标;②通过增加分区,随着系统规模的线性增加,成本也是线性增加;③当某个片区的控制中心出现问题时,只有那个片区的人挨冻,其余片区的人不受影响。
分散式控制方案的缺点在于:①个体抗风险能力差,每个片区各自为政,出现紧急情况时,无法集中力量办大事:例如某片区遭受严重的冰雪灾害,供暖系统遭到破坏,无法调动其他片区的暖气来供暖 ;②无法实现资源的优化配置,两个相邻的片区,一个电价高且自己能够生产的暖气不足,另一个电价低且生产的暖气过剩,导致片区整体舒适度较低。
集中式控制方案可以把整个系统看做一个人,有一个控制中心:大脑,多个传感器:五官和皮肤,多个执行器:四肢、铁头功、LOL酒桶的肚子。
分散式控制方案则把整个系统划分成人群,每个人都有自己的控制器和执行器,彼此之间不沟通。
在分散式控制的基础上,如果能够消除相邻片区的隔阂,互通有无,则显然能够提高整体的舒适度。倘若暖气能从某一个片区出发,总能通过各种路径,流过所有片区,则把这种方法称为分布式控制方案。
分布式控制方案兼具集中式和分散式方案的优点,又克服了它们的缺点。因而研究分布式控制方案具有较大的理论价值与实际应用价值。
根据上述分析,“烧热水”问题主要有三种控制方案:
①集中式控制:有一个控制中心,与每一个片区相连,控制所有的片区供暖设施;
②分散式控制:没有控制中心,每个片区相互独立,各玩各的;
③分布式控制:没有控制中心,相邻片区供水管道相连,且至少能找到一股热水从一个片区出发,流经整个东三省。
学术上,我们通常用 “智能体(agent)”来替换前述片区/人,集中式控制只有一个智能体。分散式控制和分布式控制均有多个agent,前者的agent互不来往,后者的agent邻里关系密切。
本系列文章主要研究多个agent的分布式控制:多智能体协同控制。
前面讲了一大串,讲到了分布式控制,但又只是文字上的扯淡,啥也不是。
如果停留在语言描述上,容易成为文学。要把它称为科学,要求我们用数学的方式去描述分布式控制,设计相应的控制律,实现我们的控制目标。
目前公认的比较早的关于多智能体系统的综述性文章是Reza Olfati-Saber在2007年撰写的文章《Consensus and Cooperation in Networked Multi-Agent Systems》(基于2003年~2007年间的文章)。在此之后,多智能体算法开始蓬勃发展。
撇开复杂的论文,我们先来看两个简单例子,理解一下分布式一致性算法。
例1、分蛋糕问题(集中式)。小多、小智、小能、小体四个人合买了一块20斤大蛋糕。小智作为智商担当负责分蛋糕,鸡贼的他切的蛋糕有的多有的少,自己拿了8斤,给女朋友小体6斤,分了小能4斤,小多拿的最少,只有2斤。小多和小能肯定不愿意,花同样的钱,出同样的力,凭什么自己分到的蛋糕少了?于是他们要求平均分。请问应该怎么分?
这问题也太简单了,一共20斤,4个人,一人称5斤不就完事了。但要注意,这是一种集中式控制方案。我们需要知道:①蛋糕总数是20斤;②一共有4个人。然后每个人的分的蛋糕=20/4=5斤。
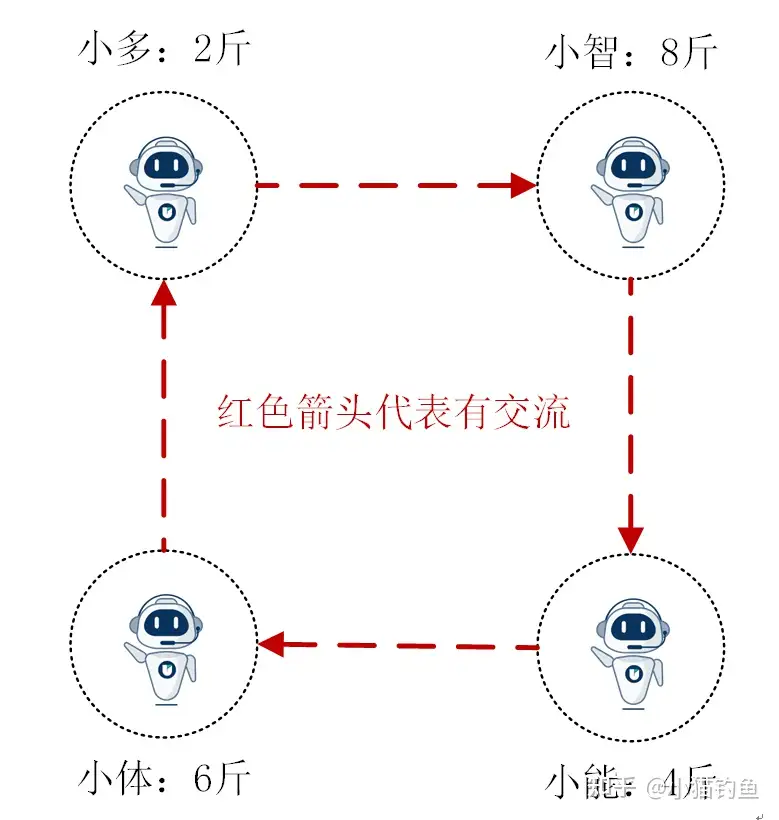
例2、分蛋糕问题(分布式)。小多、小智、小能、小体四个人合买了一块蛋糕,老板给的时候随意切了几下。各自回家后,小多发现自己只有2斤,小智有8斤,小能有4斤,小体有6斤。现在的情况是:①他们都不知道大蛋糕一共有几斤;②他们都是交了相同的钱,但是不知道一共有几个人合买;③他们都只和自己的邻居交流,交流方式如下图,且已经发现彼此数量不一样,小多很生气。问:如何在现有的交流方式下,实现蛋糕的平均分配?
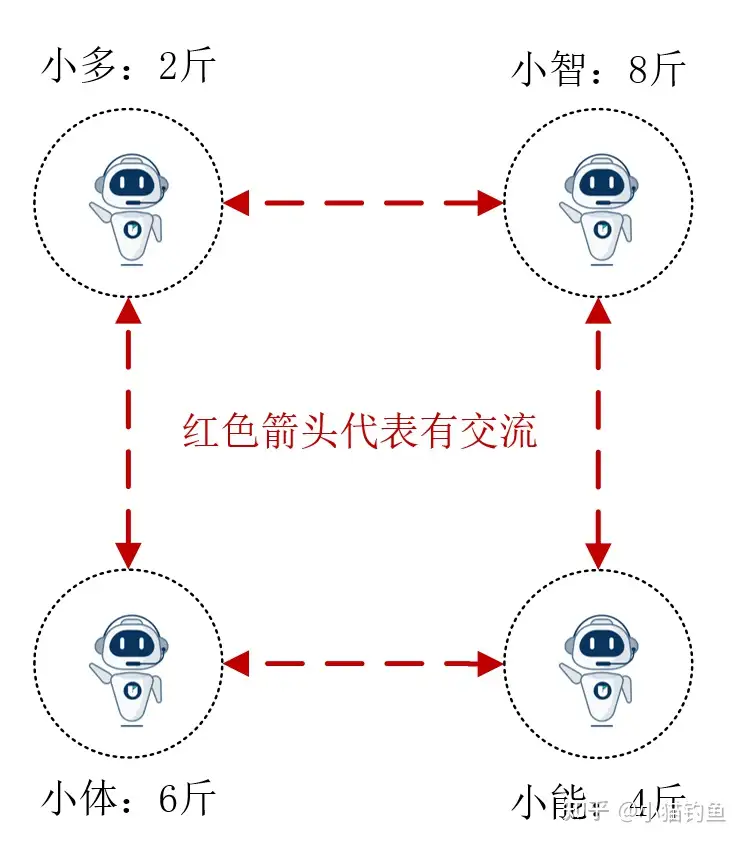
显然,由于不知道蛋糕总量和总人数,无法用简单的除法得到每个应该分配的蛋糕数。对于每个agent,已知条件是:自己和邻居的蛋糕数量。有没有一种算法能够在这样的情况下,实现蛋糕均分呢?
我们可以这样做:①每隔一段时间T,让每个agent都把自己的蛋糕量和邻居的蛋糕数相加,求平均值。②如果平均值小于自己当前蛋糕量,则将多余的量放到公共平台上,让其他agent去取;如果平均值大于当前蛋糕量,则从公共平台上去取其他agent放上去的蛋糕。
不断重复①②步骤,直到每个agent的蛋糕量不再变化,则每个agent此时的蛋糕应该就是总量的平均值。
我们用数据来看一下上述迭代过程:
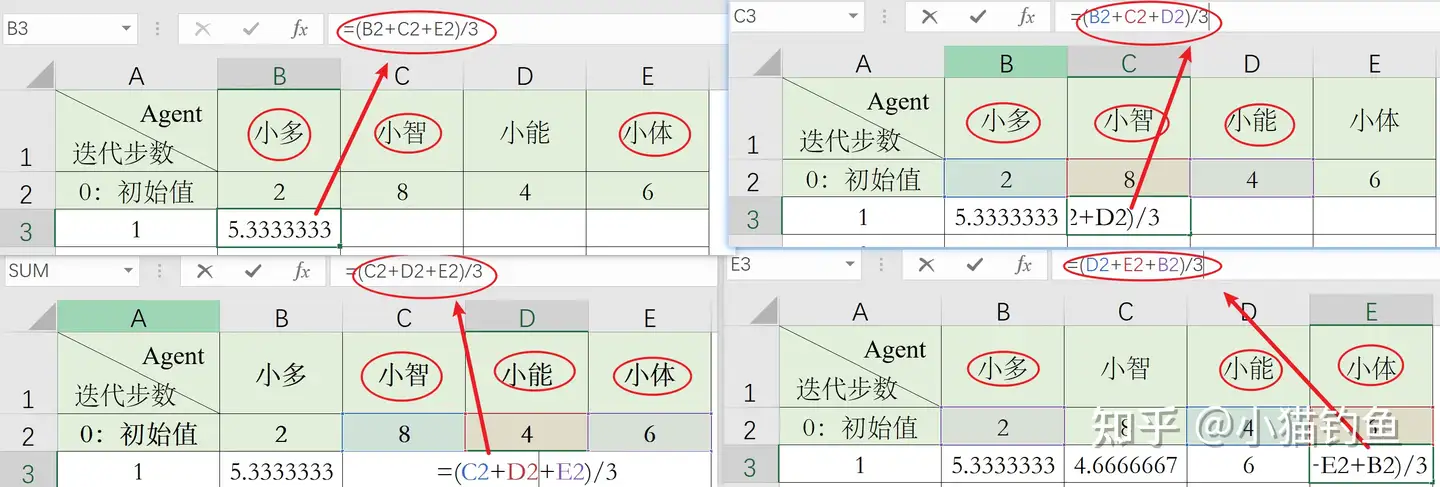
简单起见,我们在Excel中进行迭代过程。初始值记为第0步,根据前述Agent之间的交流方式可知,每个Agent下一步的值,都是上一步自身值与邻居值的平均值。完成第1步的公式输入后,直接往下拉,生成15步迭代。
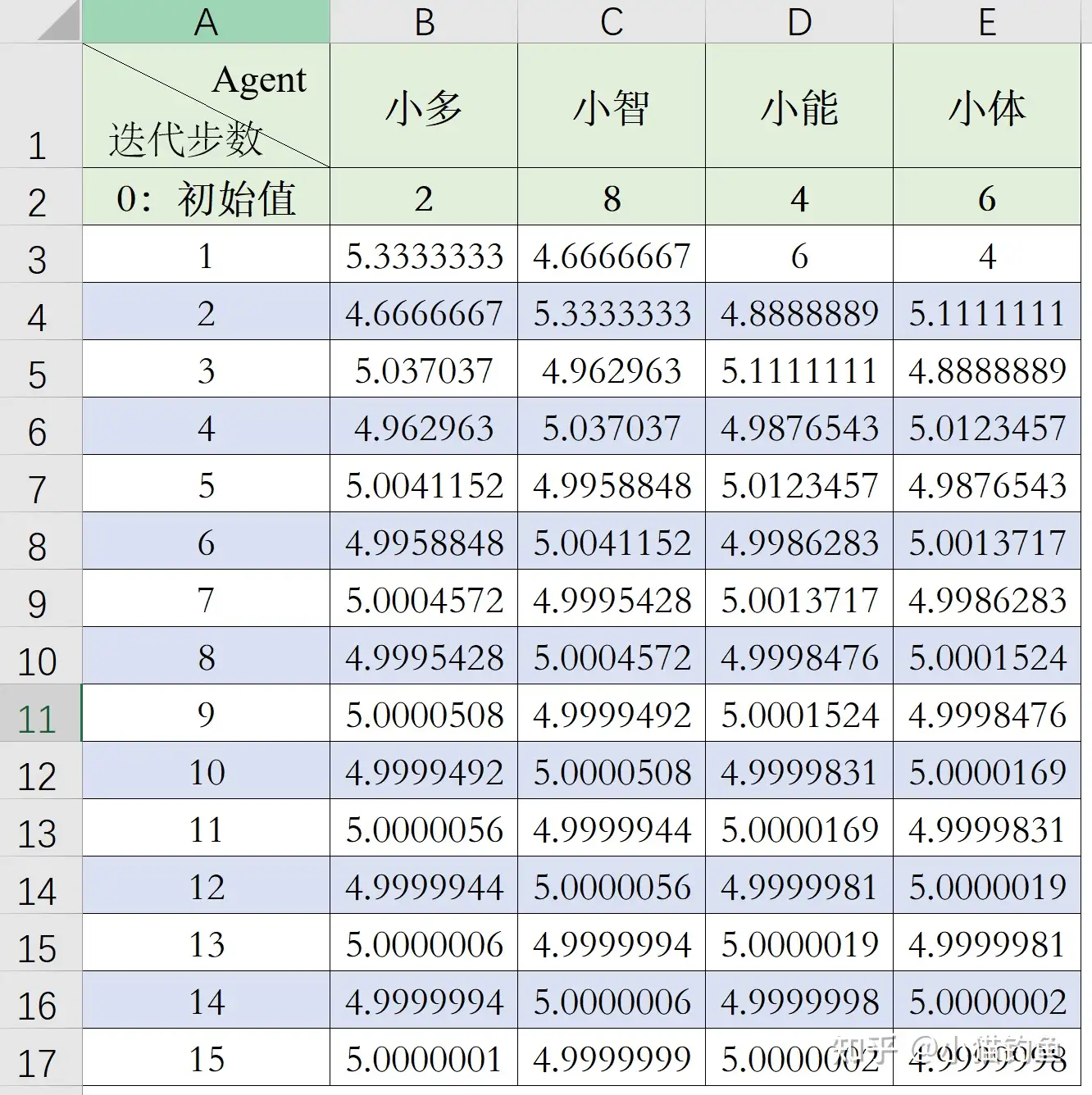
从图中可以看出,经过几次迭代后,每个人手里的蛋糕已经接近平均值5斤了。
可见,通过这种分布式的分蛋糕方式,也能实现我们平均分配蛋糕的目的。并且注意到,每个Agent都不知道系统的整体信息,我们其实是在用“局部信息”获取“整体信息”。
也可以在matlab中,进行编程。
clear;clc
N = 15;
t=1:N;
X1 = zeros(4,N);
X1(1,1) = 2;
X1(2,1) = 8;
X1(3,1) = 4;
X1(4,1) = 6;for k = 2:N
X1(1,k) = (X1(1,k-1)+X1(2,k-1)+X1(4,k-1))/3;
X1(2,k) = (X1(1,k-1)+X1(2,k-1)+X1(3,k-1))/3;
X1(3,k) = (X1(2,k-1)+X1(3,k-1)+X1(4,k-1))/3;
X1(4,k) = (X1(3,k-1)+X1(4,k-1)+X1(1,k-1))/3;
endplot(t,X1(1,:),t,X1(2,:),t,X1(3,:),t,X1(4,:))迭代过程如下图所示。
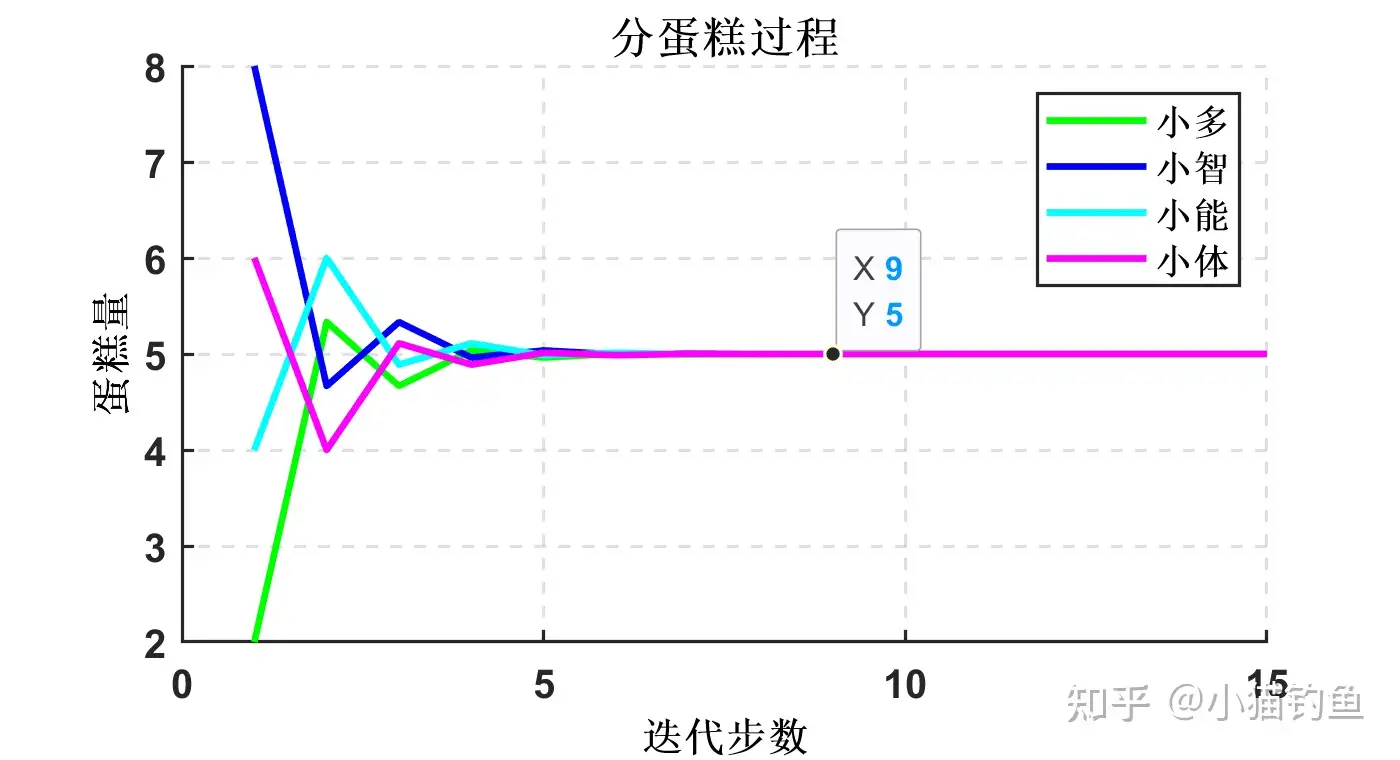
我们再来看一个多智能体协同(这里指集聚现象,flocking)的例子。

看动物世界的时候,我们观察到这些小可爱们能够神奇的聚集在一起,向某个特定的方向前进,彼此之间还不碰撞。这就启发学者提出了三条规则:①保持距离:避免邻居之间的冲突;②保持联系:避免邻居之间过于疏远;③同心同德:所有人步调一致,向一个目标进发。
简单起见,这里只考虑前两条规则。看看我们如何把“世界观:保持距离、保持联系”变成“方法论:代码”。
例3、若即若离问题。小多、小智、小能和小体四个人,一起从家里出发去学校。他们的家庭地址虽然不同,但是都要走同一条路,因此相约结伴而行。一方面他们是好朋友,一旦彼此之间的距离太远了,比如超过10米了,就要相互靠近;另一方面每个人都有自己的舒适圈,一旦彼此之间的距离太近了,比如小于0.5米了,就要相互散开一点。已知4个人的家庭地址(二维坐标)、舒适圈(0.5米)、吸引圈(10米),问:如何设计分布式控制策略,使他们最终能够保持所有人都舒适的距离一起上学?并用图形展示。
我们可以这样做:每隔一段时间T,让每个人都以10米为半径,看看里面有没有邻居。如果有邻居,判断一下他们有没有越界(距离小于0.5米),离越界的朋友远一点(离开的方向为直线后退,后退的长度为两个人之间的距离乘以系数c),离疏远的朋友近一点(接近的方向为直线靠近,靠近的长度为两个之间的距离乘以系数d)。
不断重复这个过程,直到每个人之间的距离在保持一定的范围内,则四个人都在比较舒适的距离上了。
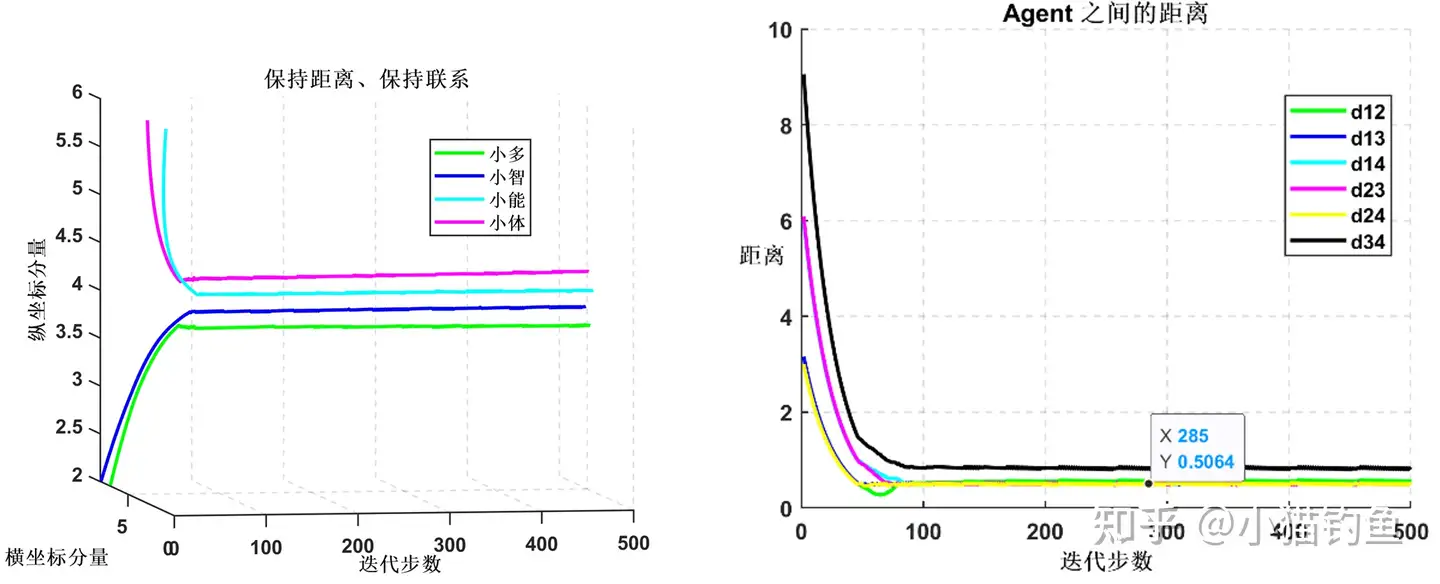
从上图中可以看出,经过一段时间的迭代后,四个人的位置处于一个比较舒适的距离上了:大于0.5,且在0.5附近。d12代表agent 1(小多)与agent 2(小智)之间的距离。
分蛋糕问题是一个典型的分布式一致性算法的例子,在控制领域中,通常可用于无线传感器网络状态估计等例子.
若即若离问题是一个典型的分布式协同算法的例子,在控制领域中,通常可用于无人机编队、机器人编队等问题。
我们再来回看一下分蛋糕问题。如果四个人之间的交流方式变成单向的,还能实现平均分配么?
答案是:可以。
那如果交流方式改成链式的呢?还能收敛到平均值么

答案是:四个人的蛋糕量会收敛到相同值,但是不是平均值。
可见,分布式一致性算法的实现与多智能体之间的交流方式密切相关。
前面的例子中,我们从文字描述出发,进行了代码编程,并实现控制目标,从文学向科学跨进了一步,但是这还不够。我们给出的策略还是不够数学,不够严谨。
从下篇教程开始,将会开始涉及大量的数学概念,从而把多智能体一致性算法建立在严密的数学推导之上。
若即若离问题详细代码:
%%
close all
clear;clc;
N = 500; %迭代步数
t = 1:N;
X1 = zeros(4,2,N);
D = 5;
X1(1,:,1) = ceil(rand(1,2)*10); % 产生随机位置
X1(2,:,1) = ceil(rand(1,2)*10);
X1(3,:,1) = floor(rand(1,2)*10);
X1(4,:,1) = floor(rand(1,2)*10);% X1(1,:,1) = [1 5]; % 给定固定位置
% X1(2,:,1) = [2 6];
% X1(3,:,1) = [4 1];
% X1(4,:,1) = [6 3];d_reject = 0.5; % 舒适圈
d_connect = 10; % 吸引圈k_connect = 0.01; % 吸引系数
k_reject = 0.03; % 排斥系数d11 = zeros(1,N); % agent之间的距离, ① d12 = d21; ② 也可以写出大矩阵形式,节省代码行数。
d12 = zeros(1,N);
d13 = zeros(1,N);
d14 = zeros(1,N);d21 = zeros(1,N);
d22 = zeros(1,N);
d23 = zeros(1,N);
d24 = zeros(1,N);d31 = zeros(1,N);
d32 = zeros(1,N);
d33 = zeros(1,N);
d34 = zeros(1,N);d41 = zeros(1,N);
d42 = zeros(1,N);
d43 =