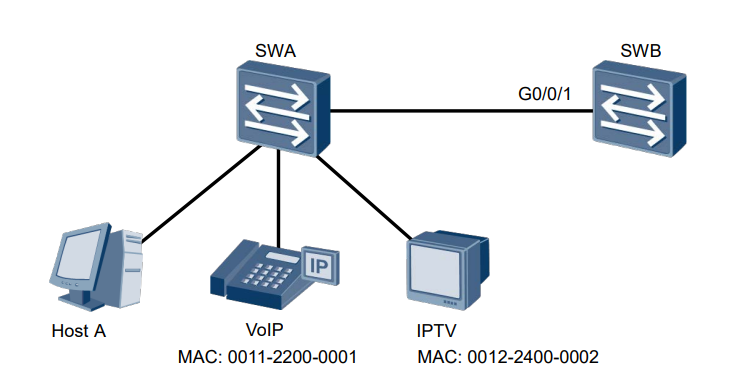
T1 变换
一道DP题,用 \(f_{i, j, 0/1}\) 来表示到了第 \(i\) 个数,总共修改了 \(j\) 次,前面的数是/不是山谷点,做 DP 即可
T2 交替
根据超大眼观察法,我们可以发现,当剩余数组大小为偶数的时候,呈现一个组合数的形式,于是使用公式 \(C_{m}^{n} = \dfrac{m!}{n!(m-n)!}\) 配合逆元求出组合数来得出。
代码难度有点高,花了25min才调出来。
#include <fstream>using namespace std;
using ll = long long;const ll kMaxN = 1e5 + 1, kMod = 1e9 + 7;ifstream cin("alternate.in");
ofstream cout("alternate.out");ll n, a[kMaxN], jie[kMaxN];ll fpow(ll a, ll b) { // 快速幂ll res = 1;while (b) {(b & 1) && (res = res * a % kMod);b >>= 1;a = a * a % kMod;}return res;
}ll C(ll m, ll n) { // 逆元求组合数return jie[m] * fpow(jie[m - n], kMod - 2) % kMod * fpow(jie[n], kMod - 2) % kMod;
}int main() {jie[0] = 1;cin >> n;for (ll i = 1; i <= n; i++) {cin >> a[i], jie[i] = jie[i - 1] * i % kMod;}ll ans = 0;if (n & 1) { // 奇数的情况for (int i = 1; i <= n; i += 2) {ans = (ans + C(n / 2, i / 2) * fpow(-1, i / 2) * a[i] % kMod) % kMod;}} else { // 偶数的情况ll ans2 = 0;for (int i = 1; i < n; i += 2) {ans = (ans + C(n / 2 - 1, i / 2) * fpow(-1, i / 2) * a[i] % kMod) % kMod;}for (int i = 2; i <= n; i += 2) {ans2 = (ans2 + C(n / 2 - 1, i / 2 - 1) * fpow(-1, i / 2 - 1) * a[i] % kMod) % kMod;}ans += ans2;}cout << (ans % kMod + kMod) % kMod << '\n';return 0;
}