哇今天做了道特别有意思的题。
编程就给了两道,第一题特别简单,a、b两个数,每次选其中一个数*2,这样操作两次,问最后得到的两数之和的期望值是多少。
简单吧?因为每次选择都有两种可能性,操作两次后就会有四种可能的结果(22)。其中有两个结果是重复的(2a, 2b),剩下两个分别是(a, 4b)和(4a, b)。把这四个结果求和除以4就是期望值。或者还有种角度,分别计算两次操作后 a 的期望和 b 的期望,把两者相加就是两数之和的期望(期望的线性性)。
第二题上来就看懵了。定义2*2的相邻元素(上下、左右)互不相同的01矩阵为好矩阵(比如[1 0 0 1]),而一个矩阵中包含好子矩阵的数量为它的权值。输入n、m,问所有 n * m 的矩阵权值的总和是多少?
啥玩意?我真的想破脑袋。后来笔试结束了才猛然醒悟,这两题是有联系的!第一题看似简单,其实正暗示了第二道题的解法:期望!
问题描述
•矩阵定义:我们考虑所有可能的 n * m 的 0-1 矩阵。
•权值定义:每个矩阵的权值是其中包含的好子矩阵的数量。
•好子矩阵定义:一个 2 * 2 的子矩阵,满足相邻元素(上下、左右)互不相同。
变量定义
•总矩阵数 N :所有可能的 n * m 矩阵的数量。N = 2n*m(因为每个元素有 2 种可能,共有 n * m 个元素)
•子矩阵位置数 K :每个矩阵中可能的 2 * 2 子矩阵的数量。K = (n - 1) * (m - 1)(因为在 n * m 的矩阵中,横向有 n - 1 个位置,纵向有 m - 1 个位置)
•好子矩阵的概率 P :随机生成的 2 * 2 子矩阵是好子矩阵的概率。P = 2/16 = 1/8(因为共有 16 种可能的 2 * 2 0-1 矩阵,其中只有 2 种是好子矩阵)
推导过程
目标:计算所有可能的 n * m 矩阵的权值总和,即所有矩阵中好子矩阵的总数量。
思路:从整体角度考虑,我们可以将问题转化为计算所有位置上好子矩阵出现的总次数。
1. 计算单个位置上的好子矩阵数量
•在单个位置上,可能的子矩阵数量等于总矩阵数 N ,因为每个矩阵在该位置上都有一个对应的子矩阵。
•在该位置上,好子矩阵的总数量为: N * P(每个矩阵在该位置上有一个子矩阵,成为好子矩阵的概率为 P )
2. 计算所有位置上的好子矩阵数量
•总的位置数为 K ,每个位置独立且等价。
•所有位置上的好子矩阵总数为:总权值 = K * N * P
逻辑解释
有人可能疑惑了,每个位置怎么会独立呢?相邻子矩阵不是有共享的元素吗?
这里就要引入关键概念:期望的线性性。
期望的线性性是指,对于任意随机变量的和,其期望等于这些随机变量的期望之和,即使这些随机变量之间有相关性。这一点非常重要。
在我们的情境中:
•随机变量定义:对于矩阵中的每个可能的 2 * 2 子矩阵位置,我们定义一个指示变量 Xi ,如果该位置上的子矩阵是好子矩阵,其值为 1 ,否则为 0。
•总权值:所有矩阵的总权值等于所有 Xi 的和。
尽管这些 Xi 之间存在相关性(因为子矩阵共享元素),但在计算期望时,这种相关性并不影响总期望值的计算,期望的线性性仍然成立。
对于每个位置 i :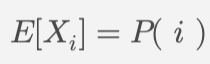
总期望值: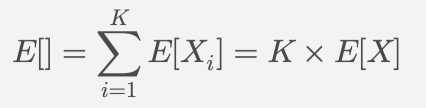
其中 E[X] 是任意一个位置上子矩阵为好子矩阵的概率 P 。