题意简述
一个长度为 \(n\) 的实数序列 \(a_i\)，其中 \(a_i\) 为 \([l_i, r_i]\) 中独立均匀随机选取的实数。你只能通过交换相邻两个数，使得 \(a_i\) 单调不降。你需要求出你最少操作次数的期望，对 \(M = 998244353\) 取模。
\(1 \leq n \leq 10^6\)，\(0 \leq l_i \lt r_i \leq 10^{18}\)。
题目分析
由于 \(l_i \lt r_i\)，所以两个数 \(a_i = a_j\) 的概率为 \(0\)，对答案没有贡献。我们的问题就是 \(a_i\) 的逆序对个数的期望了。
由数学期望的性质，我们考虑每一对 \(i < j\) 对答案的贡献，是这对 \((i, j)\) 为逆序对的概率，乘上 \(1\)。那么累加后，答案即为 \(\sum \operatorname{P}(a_i > a_j)\)。
我们先来考虑 \(\Theta(n^2)\) 的算法，问题变成了如何求 \(p \in [l_1, r_i] > q \in [l_2, r_2]\) 的概率。一个想法是对这两段区间的关系进行分讨。
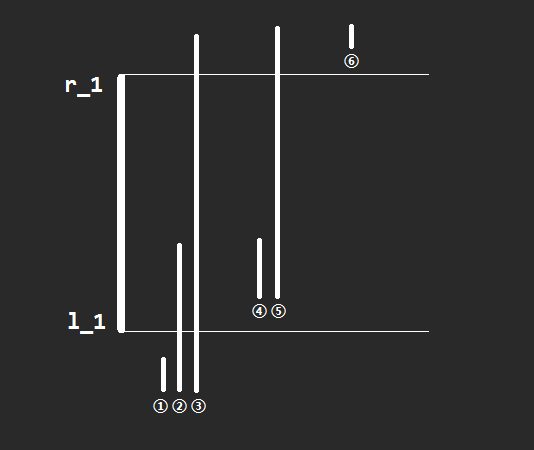
其实并不复杂？因为 \((1, 6), (2, 5), (3, 4)\) 是左右对称的，我们解决一半，另一半倒着做一遍，再取概率另一半即可。我们不妨考虑 \((1, 4, 5)\)。
\(1\) 很容易计算，使用树状数组扫一下就行了。
关于 \(4\)，我们考虑两种情况，第一种是 \(a_i\) 取到了 \(r_j \sim r_i\)，此时无论 \(a_j\) 的取值，总有 \(a_i \gt a_j\)；第二种是 \(a_i\) 和 \(a_j\) 同时取到了 \(l_j \sim r_j\)，此时问题为两个随机变量 \(\lambda, \varphi\) 取值范围相同，求 \(\lambda \gt \varphi\) 的概率，结论是 \(\dfrac{1}{2}\)。
点击展开进一步说明
不妨假设取值范围为 \([l, r]\)，不失一般性，不妨整体下移 \(l\)，即考虑 \([0, r - l]\)，记 \(p = r - l\)。
对于一个确定的 \(\lambda\)，随机出 \(\varphi \lt \lambda\) 的概率为 \(\operatorname{P}(\varphi \lt \lambda \mid \lambda) = \dfrac{\lambda}{p}\)。
\[\begin{aligned}
\operatorname{P}(\lambda \gt \varphi) &= \int _ {0} ^ p \dfrac{1}{p} \dfrac{\lambda}{p} \mathrm{d} \lambda \\&= \dfrac{1}{p^2} \int _ {0} ^ p \lambda \mathrm{d} \lambda \\&= \dfrac{1}{p^2} \dfrac{p^2}{2} \\&= \dfrac{1}{2}
\end{aligned}
\]
如果你不太理解，请阅读后文图形化的说明。
此时，列式表达即为 \({\displaystyle \frac{1}{2}\frac{\operatorname{len}_j}{\operatorname{len}_i}+\frac{r_i - r_j}{\operatorname{len}_i} = \frac{1}{2\operatorname{len}_i}\operatorname{len}_j+\frac{1}{\operatorname{len}_i}\left(r_i - r_j\right)}\)。
关于 \(5\)，只用当 \(a_i, a_j\) 都取到 \(l_j \sim r_i\) 时，才有可能成为逆序对，概率为 \({\displaystyle \frac{r_i - l_j}{\operatorname{len}_i} \frac{r_i - l_j}{\operatorname{len}_j} \frac{1}{2}}\)。我们来一步步化简：
\[\begin{aligned}
&\quad \ \frac{r_i - l_j}{\operatorname{len}_i} \frac{r_i - l_j}{\operatorname{len}_j} \frac{1}{2} \\
&= \frac{1}{2\operatorname{len}_i} \frac{r_i^2 -l_j^2 - 2r_il_j}{\operatorname{len}_j} \\
&= \frac{1}{2\operatorname{len}_i}\left(\frac{r_i^2}{\operatorname{len}_j}-\frac{l_j^2}{\operatorname{len}_j}-\frac{2r_il_j}{\operatorname{len}_j}\right) \\
&= \frac{1}{2\operatorname{len}_i}\left(r_i^2\frac{1}{\operatorname{len}_j}-\frac{l_j^2}{\operatorname{len}_j}-2r_i\frac{l_j}{\operatorname{len}_j}\right)
\end{aligned}
\]
对于每一种情况，我们都将其拆成了多个关于 \(i\) 和关于 \(j\) 的项乘积的形式，形如 \(v_i c_j\)。我们从右向左扫，用一个数据结构维护 \(\sum c_j\)，查询满足特定条件的 \(\sum c_j\)，贡献为 \(\sum v_i c_j = v_i \sum c_j\)。
这样的 \(c_j\) 有 \(6\) 种，分别为：
- \(1\)；
- \(\operatorname{len}_j\)；
- \(r_j\)；
- \(\dfrac{1}{\operatorname{len}_j}\)；
- \(\dfrac{l_j^2}{\operatorname{len}_j}\)；
- \(\dfrac{l_j}{\operatorname{len}_j}\)；
怎么样，是心动的感觉~
问题就出在了「特定条件」，无论是 \(4\) 还是 \(5\)，我们对 \(j\) 的 \(l_j, r_j\) 都有限定。这样的三维偏序问题，就不得不 CDQ 或树套树了，但无论如何，\(\Theta(n \log ^ 2 n)\) 的时间是我们无法接受的。
点击展开题外话
其实原题 \(n \leq 10^5\)，也不是没有可能，如果你帮我把文末 \(25.7\)KiB、\(736\) 行的性感代码卡过了，请收下我一拜！
似乎不好整，换个方法吧。我们想办法越过对于 \(a_i, a_j\) 的取值区间的关系的分析，这也是我们上述算法瓶颈之根本所在。发现是连续变量的二元关系，和概率有关，应该需要放到平面直角坐标系上观察，且和面积要搭上边。
我们把横轴设为 \(a_i\)，纵轴设为 \(a_j\)，那么合法的 \((a_i, a_j)\) 构成了平面上一个矩形。直线 \(a_i = a_j\) 下方的部分就表示 \(a_i \gt a_j\)。
动手试试吧！
紫色部分的面积比上总面积，就是 \(a_i > a_j\) 的概率，问题变成求这个不规则的图形的面积。如果分类讨论又要回到上面了，那我们换一种思路，用容斥，也就是小奥中一种方法，用规则图形拼出不规则图形。我们这里规则图形是什么？很显然，和 \(y = x\) 和横轴构成的三角形有关。用若干这样的三角形就能拼凑出紫色部分。这很类似二位前缀和，我们记 \(g(\lambda, \varphi)\) 表示，\(x \in [0, \lambda], y \in [0, \varphi]\) 的矩形内，\(x \gt y\) 部分的面积。那么 \(a_i \gt a_j\) 的概率即为：
\[\frac{g(r_i, r_j) - g(r_i, l_j) - g(l_i, r_j) + g(l_i, l_j)}{\operatorname{len}_i \operatorname{len}_j}
\]
接下来研究 \(g(\lambda, \varphi)\)，尝试得到一个简单的表达式。
动手试试吧！
此时好像要分 \(\lambda \leq \varphi\)，\(\lambda \gt \varphi\) 两种情况讨论了，但比上面 \(6\) 类简单多了，不是吗？
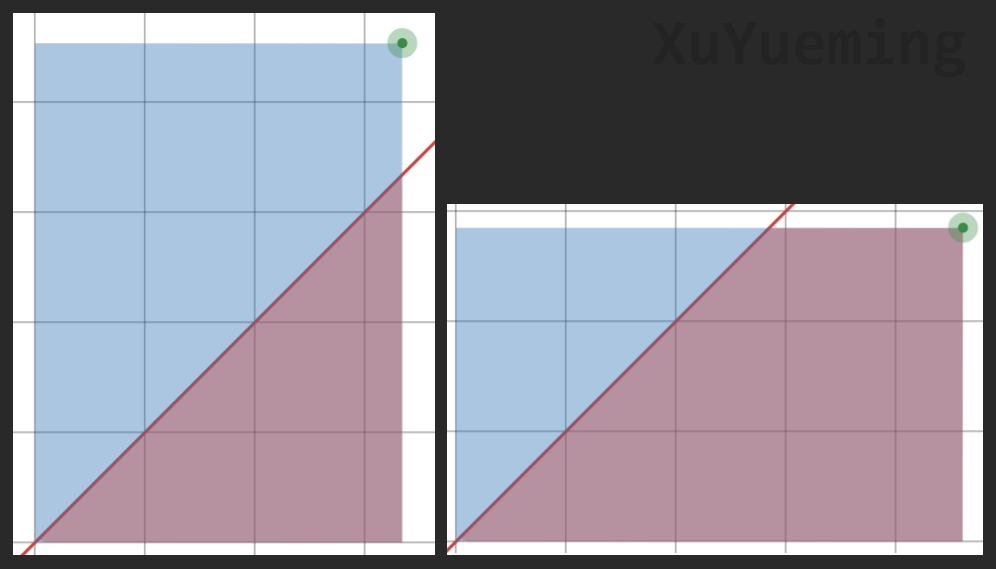
得到：
\[g(\lambda, \varphi) = \left\{\begin{matrix}
\dfrac{\lambda^2}{2} & \text{if} \ \lambda \leq \varphi\\
\varphi \lambda - \dfrac{\varphi^2}{2} & \text{if} \ \lambda \gt \varphi\\
\end{matrix}\right.
\]
关于上文「进一步说明」
注意到，当 \(\lambda = \varphi\) 的时候，满足条件部分恰好是整个正方形的 \(\dfrac{1}{2}\)，也就是我们的结论。
看看我们要算的：
\[\frac{\Big(\frac{g(r_i, r_j)}{\operatorname{len}_j} - \frac{g(r_i, l_j)}{\operatorname{len}_j}\Big) - \Big(\frac{g(l_i, r_j)}{\operatorname{len}_j} - \frac{g(l_i, l_j)}{\operatorname{len}_j}\Big)}{\operatorname{len}_i}
\]
显然从右往左扫，需要用数据结构维护 \(j > i\) 的信息。我们只需要用 \(3\) 个树状数组维护：
- \(\dfrac{1}{\operatorname{len}_j}\)；
- \(\dfrac{\varphi}{\operatorname{len}_j}\)；
- \(\dfrac{\varphi^2}{\operatorname{len}_j}\)。
其中 \(\varphi\) 是关于 \(l_j, r_j\) 的变量。由于我们查询的时候并不关心是 \(l_j\) 还是 \(r_j\)，只关心 \(l_j\) 前的系数是 \(-1\)，那么我们在插入时，就插入 \(-l_j\) 即可。查询的时候就很方便了，分讨一下，用 \(r_i\) 的答案减去 \(l_i\) 的答案即可。
时间复杂度 \(\Theta(n \log nM)\)，空间复杂度 \(\Theta(n)\)。
代码
根据原题 \(0 \leq l_i \lt r_i \leq 10^8\)。
$25.7$KiB、$736$ 行的性感代码
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast", "inline", "-ffast-math")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <ctime>
using namespace std;char ST;const int MAX = 1 << 26;
char buf[MAX], *p = buf;
#ifdef XuYueming
# define fread(_, __, ___, ____)
#else
# define getchar() *p++
#endif
#define isdigit(x) ('0' <= x && x <= '9')
#define __yzh__(x) for (; x isdigit(ch); ch = getchar())
template <typename T>
inline void read(T &x) {x = 0; char ch = getchar(); __yzh__(!);__yzh__( ) x = (x << 3) + (x << 1) + (ch ^ 48);
}constexpr int N = 100010;
constexpr int mod = 998244353;
constexpr int inv2 = (mod + 1) >> 1;
using lint = long long;
using ull = unsigned lint;constexpr __int128_t _base = ((__int128_t)(1) << 64) / mod;
inline long long mol(long long x){return x - mod * (_base * x >> 64);
}inline int add(int a, int b) {return a + b >= mod ? a + b - mod : a + b;
}
inline int sub(int a, int b) {return a - b < 0 ? a - b + mod : a - b;
}
inline int mul(int a, int b) {return mol(1ll * a * b);
}
inline int pow(int a, int b) {int res = 1;for (; b; b >>= 1, a = mul(a, a))if (b & 1) res = mul(res, a);return res;
}
inline int inv(int x) {return pow(x, mod - 2);
}int n;
int L[N], R[N];namespace pts60 {inline bool check() {return n <= 5000;}inline int in(int a, int b) {// a 里挑 breturn mul(b, inv(a));}int big(int l1, int r1, int l2, int r2) {// [l1, r1] > [l2, r2]if (l1 > l2) return sub(1, big(l2, r2, l1, r1));if (l2 >= r1) return 0;if (r2 <= r1) {int res = 0;res = add(res, in(r1 - l1, r1 - r2));res = add(res, mul(inv2, in(r1 - l1, r2 - l2)));return res;} else {return mul(inv2, mul(in(r1 - l1, r1 - l2), in(r2 - l2, r1 - l2)));}}void solve() {int ans = 0;for (int i = 1; i <= n; ++i)for (int j = i + 1; j <= n; ++j) {ans = add(ans, big(L[i], R[i], L[j], R[j]));}printf("%d", ans);}
}namespace l0 {inline bool check() {for (int i = 1; i <= n; ++i)if (L[i] != 0) return false;return true;}int real[N], V;struct Bit_Tree {static inline int lowbit(int x) {return x & -x;}int tree[N];inline void modify(int p, int v) {for (int i = p; i <= V; i += lowbit(i))tree[i] = add(tree[i], v);}inline int query(int p) {int res = 0;for (int i = p; i; i -= lowbit(i))res = add(res, tree[i]);return res;}} yzh, cnter;void solve() {for (int i = 1; i <= n; ++i)real[++V] = R[i];sort(real + 1, real + V + 1);V = unique(real + 1, real + V + 1) - real - 1;int ans = 0;for (int i = n; i >= 1; --i) {int r = lower_bound(real + 1, real + V + 1, R[i]) - real;ans = add(ans, cnter.query(r));ans = sub(ans, mul(mul(inv2, inv(R[i])), yzh.query(r)));yzh.modify(r, R[i]);cnter.modify(r, 1);}memset(yzh.tree, 0x00, sizeof (yzh.tree));for (int i = 1; i <= n; ++i) {int r = lower_bound(real + 1, real + V + 1, R[i]) - real;ans = add(ans, mul(mul(inv2, inv(R[i])), yzh.query(r - 1)));yzh.modify(r, R[i]);}printf("%d", ans);}
}namespace yzh520 {#define fint unsigned// using fint = unsigned; // maybe unsigned is faster than signedconstexpr fint mod = 998244353;constexpr fint inv2 = (mod + 1) >> 1;constexpr __int128_t _base = ((__int128_t)(1) << 64) / (signed)mod;inline long long mol(long long x){// return x % mod;return x - 1ll * (signed)mod * (_base * x >> 64);}inline fint add(fint a, fint b) {return a + b >= mod ? a + b - mod : a + b;}// #undef fint// #define fint intinline fint sub(fint a, fint b) {// if (a >= mod) cerr << "A " << a << endl, printf("%p,%p\n", __builtin_return_address(0), __builtin_return_address(1)), throw -1;// if (b >= mod) cerr << "B " << b << endl, printf("%p,%p\n", __builtin_return_address(0), __builtin_return_address(1)), throw -1;// a %= mod, b %= mod;return a < b ? a + mod - b : a - b;}// #undef fint// #define fint unsignedinline fint mul(fint a, fint b) {return 1llu * a * b % mod;// return mol(1ll * (signed)a * (signed)b);}inline fint pow(fint a, fint b) {fint res = 1;for (; b; b >>= 1, a = mul(a, a))if (b & 1) res = mul(res, a);return res;}inline fint inv(fint x) {return pow(x, mod - 2);}fint ll[N], rr[N], invlen[N];fint real[N << 1], V;struct Bit_Tree {static constexpr inline fint lowbit(fint x) {return x & -x;}fint tree[N << 1];inline void modify(fint p, fint v) {for (register fint i = p; i <= V; i += lowbit(i))tree[i] = add(tree[i], v);}inline fint query(fint p) {fint res = 0;for (register fint i = p; i; i -= lowbit(i))res = add(res, tree[i]);return res;}// inline void clear() {// memset(tree, 0x00, sizeof (int) * (V + 10));// }} cnter;namespace New_Segment_Tree {// struct New_Segment_Tree {struct node {fint lson, rson, sum[6];} tree[N * 520];fint tot, sum[6], p, l, r;void modify(fint &idx, fint trl, fint trr) {if (!idx) tree[idx = ++tot] = {};tree[idx].sum[0] = add(tree[idx].sum[0], sum[0]);tree[idx].sum[1] = add(tree[idx].sum[1], sum[1]);tree[idx].sum[2] = add(tree[idx].sum[2], sum[2]);tree[idx].sum[3] = add(tree[idx].sum[3], sum[3]);tree[idx].sum[4] = add(tree[idx].sum[4], sum[4]);tree[idx].sum[5] = add(tree[idx].sum[5], sum[5]);if (trl == trr) return;fint mid = (trl + trr) >> 1;if (p <= mid) modify(tree[idx].lson, trl, mid);else modify(tree[idx].rson, mid + 1, trr);}void query_add(fint idx, fint trl, fint trr) {if (l <= trl && trr <= r) {sum[0] = add(sum[0], tree[idx].sum[0]);sum[1] = add(sum[1], tree[idx].sum[1]);sum[2] = add(sum[2], tree[idx].sum[2]);sum[3] = add(sum[3], tree[idx].sum[3]);sum[4] = add(sum[4], tree[idx].sum[4]);sum[5] = add(sum[5], tree[idx].sum[5]);return;}fint mid = (trl + trr) >> 1;if (l <= mid && tree[idx].lson) query_add(tree[idx].lson, trl, mid);if (r > mid && tree[idx].rson) query_add(tree[idx].rson, mid + 1, trr);}void query_sub(fint idx, fint trl, fint trr) {if (l <= trl && trr <= r) {sum[0] = sub(sum[0], tree[idx].sum[0]);sum[1] = sub(sum[1], tree[idx].sum[1]);sum[2] = sub(sum[2], tree[idx].sum[2]);sum[3] = sub(sum[3], tree[idx].sum[3]);sum[4] = sub(sum[4], tree[idx].sum[4]);sum[5] = sub(sum[5], tree[idx].sum[5]);return;}fint mid = (trl + trr) >> 1;if (l <= mid && tree[idx].lson) query_sub(tree[idx].lson, trl, mid);if (r > mid && tree[idx].rson) query_sub(tree[idx].rson, mid + 1, trr);}};namespace Segment_Tree {// struct Segment_Tree {fint tree[N << 1];// unsigned tree[N << 1];// New_Segment_Tree tr;inline void clear() {memset(tree + 1, 0x00, sizeof (fint) * V);New_Segment_Tree::tot = 0;}inline void modify(fint l, fint r, fint L, fint R) {New_Segment_Tree::sum[0] = R - L;New_Segment_Tree::sum[1] = R;New_Segment_Tree::sum[4] = 1;New_Segment_Tree::sum[5] = inv(R - L);New_Segment_Tree::sum[3] = mul(L, New_Segment_Tree::sum[5]);New_Segment_Tree::sum[2] = mul(New_Segment_Tree::sum[3], L);New_Segment_Tree::p = r;for (register fint i = l; i <= V; i += Bit_Tree::lowbit(i))New_Segment_Tree::modify(tree[i], 1, V);}inline void query(fint ll, fint lr, fint rl, fint rr) {New_Segment_Tree::sum[0] = New_Segment_Tree::sum[1] = New_Segment_Tree::sum[2] = New_Segment_Tree::sum[3] = New_Segment_Tree::sum[4] = New_Segment_Tree::sum[5] = 0;if (ll > lr || rl > rr) return;New_Segment_Tree::l = rl, New_Segment_Tree::r = rr, --ll;for (; lr > ll; lr -= Bit_Tree::lowbit(lr)) New_Segment_Tree::query_add(tree[lr], 1, V);for (; ll > lr; ll -= Bit_Tree::lowbit(ll)) New_Segment_Tree::query_sub(tree[ll], 1, V);}// } yzh;}void solve() {for (register fint i = 1; i <= n; ++i) {real[++V] = L[i];real[++V] = R[i];}sort(real + 1, real + V + 1);V = unique(real + 1, real + V + 1) - real - 1;register fint ans = 0;for (register fint i = n; i; --i) {ll[i] = lower_bound(real + 1, real + V + 1, L[i]) - real;rr[i] = lower_bound(real + 1, real + V + 1, R[i]) - real;ans += cnter.query(ll[i]);cnter.modify(rr[i], 1);}fprintf(stderr, "\nTime used %.2lfs. (start)\n", clock() * 1. / CLOCKS_PER_SEC);for (register fint i = n, inv_len_i, TTT, inv2len; i; --i) {inv_len_i = invlen[i] = inv(R[i] - L[i]), inv2len = mul(inv2, inv_len_i);Segment_Tree::query(ll[i], rr[i], ll[i], rr[i]);ans = add(ans, mul(inv_len_i, sub(mul(New_Segment_Tree::sum[4], R[i]), New_Segment_Tree::sum[1])));ans = add(ans, mul(inv2len, New_Segment_Tree::sum[0]));if (rr[i] != V) {Segment_Tree::query(ll[i], rr[i], rr[i] + 1, V);TTT = mul(mul(R[i], R[i]), New_Segment_Tree::sum[5]);TTT = sub(TTT, mul(mul(2u, R[i]), New_Segment_Tree::sum[3]));TTT = add(TTT, New_Segment_Tree::sum[2]);TTT = mul(TTT, inv2len);ans = add(ans, TTT);}Segment_Tree::modify(ll[i], rr[i], L[i], R[i]);}fprintf(stderr, "\nTime used %.2lfs. (half)\n", clock() * 1. / CLOCKS_PER_SEC);Segment_Tree::clear();for (register fint i = 1, inv_len_i, TTT, inv2len; i <= n; ++i) {inv_len_i = invlen[i], inv2len = mul(inv2, inv_len_i);if (ll[i] + 1 < rr[i]) {Segment_Tree::query(ll[i] + 1, rr[i], ll[i] + 1, rr[i]);ans = add(ans, New_Segment_Tree::sum[4]);ans = sub(ans, mul(inv_len_i, sub(mul(New_Segment_Tree::sum[4], R[i]), New_Segment_Tree::sum[1])));ans = sub(ans, mul(inv2len, New_Segment_Tree::sum[0]));}if (rr[i] != V && ll[i] + 2 <= rr[i]) {Segment_Tree::query(ll[i] + 1, rr[i] - 1, rr[i] + 1, V);TTT = mul(mul(2u, R[i]), New_Segment_Tree::sum[3]);TTT = sub(TTT, mul(mul(R[i], R[i]), New_Segment_Tree::sum[5]));TTT = sub(TTT, New_Segment_Tree::sum[2]);TTT = mul(TTT, inv2len);TTT = add(New_Segment_Tree::sum[4], TTT);ans = add(ans, TTT);}Segment_Tree::modify(ll[i], rr[i], L[i], R[i]);}printf("%u", ans);fprintf(stderr, "\nTime used %.2lfs.\n", clock() * 1. / CLOCKS_PER_SEC);}
}#if false && defined xym_loves_yzh
namespace yzh520 {int ll[N], rr[N];int real[N << 1], V;struct Bit_Tree {static inline int lowbit(int x) {return x & -x;}int tree[N << 1];inline void modify(int p, int v) {for (int i = p; i <= V; i += lowbit(i))tree[i] = add(tree[i], v);}inline int query(int p) {int res = 0;for (int i = p; i; i -= lowbit(i))res = add(res, tree[i]);return res;}inline void clear() {memset(tree, 0x00, sizeof (int) * (V + 10));}} cnter;struct New_Segment_Tree {// unordered_map<int, int> tr[N * 20][6];// int sum[6], tot;// void modify(int &idx, [[maybe_unused]] int _, [[maybe_unused]] int __, int p) {// if (!idx) {// idx = ++tot;// for (int j = 0; j < 6; ++j)// tr[idx][j].clear();// }// for (int j = 0; j < 6; ++j) {// for (int i = p; i <= V; i += Bit_Tree::lowbit(i))// tr[idx][j][i] += sum[j];// }// }// void query(int idx, int p, int f) {// if (!idx) return;// for (int j = 0; j < 6; ++j) {// for (int i = p; i; i -= Bit_Tree::lowbit(i))// if (tr[idx][j].count(i))// sum[j] += tr[idx][j][i];// }// }// void query(int idx, [[maybe_unused]] int _, [[maybe_unused]] int __, int l, int r) {// query(idx, r, 1);// query(idx, l - 1, -1);// }struct node {int lson, rson, sum[6];} tree[N * 520]; // more----------------------------------------int tot, sum[6];void modify(int &idx, int trl, int trr, int p) {if (trl > p || trr < p) return;if (!idx) tree[idx = ++tot] = {};for (int i = 0; i < 6; ++i)tree[idx].sum[i] = add(tree[idx].sum[i], sum[i]);if (trl == trr) return;int mid = (trl + trr) >> 1;modify(tree[idx].lson, trl, mid, p);modify(tree[idx].rson, mid + 1, trr, p);}void query(int idx, int trl, int trr, int l, int r) {if (trl > r || trr < l || !idx) return;if (l <= trl && trr <= r) {for (int i = 0; i < 6; ++i)sum[i] = add(sum[i], tree[idx].sum[i]);return;}int mid = (trl + trr) >> 1;query(tree[idx].lson, trl, mid, l, r);query(tree[idx].rson, mid + 1, trr, l, r);}};struct Segment_Tree {#define lson (idx << 1 )#define rson (idx << 1 | 1)int tree[N << 3];New_Segment_Tree tr;void build(int idx, int l, int r) {tree[idx] = 0;if (l == r) return;int mid = (l + r) >> 1;build(lson, l, mid);build(rson, mid + 1, r);}void clear() {tr.tot = 0;build(1, 1, V);}void modify(int idx, int trl, int trr, int l, int r) {if (trl > l || trr < l) return;tr.modify(tree[idx], 1, V, r);if (trl == trr) return;int mid = (trl + trr) >> 1;modify(lson, trl, mid, l, r);modify(rson, mid + 1, trr, l, r);}void modify(int l, int r, int L, int R) {tr.sum[0] = R - L;tr.sum[1] = R;tr.sum[4] = 1;tr.sum[5] = inv(R - L);tr.sum[3] = mul(L, tr.sum[5]);tr.sum[2] = mul(tr.sum[3], L);// cout << "update len " << tr.sum[0] << endl;modify(1, 1, V, l, r);}void query(int idx, int trl, int trr, int ll, int lr, int rl, int rr) {if (trl > lr || trr < ll) return;if (ll <= trl && trr <= lr) return tr.query(tree[idx], 1, V, rl, rr);int mid = (trl + trr) >> 1;query(lson, trl, mid, ll, lr, rl, rr);query(rson, mid + 1, trr, ll, lr, rl, rr);}void query(int ll, int lr, int rl, int rr) {tr.sum[0] = tr.sum[1] = tr.sum[2] = tr.sum[3] = tr.sum[4] = tr.sum[5] = 0;if (ll > lr || rl > rr) {// puts("return in query!!!!!");return;}query(1, 1, V, ll, lr, rl, rr);}#undef lson#undef rson} yzh;void solve() {for (int i = 1; i <= n; ++i) {real[++V] = L[i];real[++V] = R[i];}sort(real + 1, real + V + 1);V = unique(real + 1, real + V + 1) - real - 1;for (int i = 1; i <= n; ++i) {ll[i] = lower_bound(real + 1, real + V + 1, L[i]) - real;rr[i] = lower_bound(real + 1, real + V + 1, R[i]) - real;// cout << ll[i] << ' ' << rr[i] << endl;}int ans = 0;for (int i = n; i >= 1; --i) {ans += cnter.query(ll[i]);cnter.modify(rr[i], 1);}// printf("ans = %d\n", ans);// cnter.clear();for (int i = n; i >= 1; --i) {// cout << "i = " << i << endl;int inv_len_i = inv(R[i] - L[i]);yzh.query(ll[i], rr[i], ll[i], rr[i]);ans = add(ans, mul(inv_len_i, sub(mul(yzh.tr.sum[4], R[i]), yzh.tr.sum[1])));ans = add(ans, mul(mul(inv2, inv_len_i), yzh.tr.sum[0]));// if (i == 1) printf(">>> %d\n", ans);if (rr[i] != V// && i == 1) {yzh.query(ll[i], rr[i], rr[i] + 1, V);// cout << "∑ len = " << yzh.tr.sum[0] << endl;// cout << "∑ R = " << yzh.tr.sum[1] << endl;// cout << "∑ L / len = " << yzh.tr.sum[3] << endl;// cout << "∑ L^2 / len = " << yzh.tr.sum[2] << endl;// cout << "cnt = " << yzh.tr.sum[4] << endl;int TTT = 0;TTT = add(TTT, mul(mul(R[i], R[i]), yzh.tr.sum[5]));TTT = sub(TTT, mul(mul(2, R[i]), yzh.tr.sum[3]));TTT = add(TTT, yzh.tr.sum[2]);TTT = mul(TTT, mul(inv2, inv_len_i));ans = add(ans, TTT);// printf(">>> %d\n", ans);// if (i == 1) {// printf(">>> %d\n", inv(mul(inv(mul(R[i], R[i])), yzh.tr.sum[0])));// printf(">>> %d\n", mul(mul(2, R[i]), yzh.tr.sum[3]));// // printf(">>> %d\n", yzh.tr.sum[3]);// printf(">>> %d\n", yzh.tr.sum[2]);// }}yzh.modify(ll[i], rr[i], L[i], R[i]);// printf("anssss = %d\n", ans);}// printf("ans = %d\n", ans);// puts("---------------------------------------------");yzh.clear();for (int i = 1; i <= n; ++i) {int inv_len_i = inv(R[i] - L[i]);// if (ll[i] + 1 <= rr[i] - 1) {yzh.query(ll[i] + 1, rr[i], ll[i] + 1, rr[i]);ans = add(ans, yzh.tr.sum[4]);ans = sub(ans, mul(inv_len_i, sub(mul(yzh.tr.sum[4], R[i]), yzh.tr.sum[1])));ans = sub(ans, mul(mul(inv2, inv_len_i), yzh.tr.sum[0]));// }// if (i == 3) {// for (int j = 0; j < 5; ++j)// printf("sum[%d] = %d\n", j, yzh.tr.sum[j]);// }if (rr[i] != V && ll[i] + 1 <= rr[i] - 1) {yzh.query(ll[i] + 1, rr[i] - 1, rr[i] + 1, V);int TTT = 0;TTT = sub(TTT, mul(mul(R[i], R[i]), yzh.tr.sum[5]));TTT = add(TTT, mul(mul(2, R[i]), yzh.tr.sum[3]));TTT = sub(TTT, yzh.tr.sum[2]);TTT = mul(TTT, mul(inv2, inv_len_i));TTT = add(yzh.tr.sum[4], TTT);// printf(">>> %d\n", TTT);ans = add(ans, TTT);}yzh.modify(ll[i], rr[i], L[i], R[i]);// printf("%d: ans = %d\n", i, ans);}printf("%d", ans);// yzh.clear();// for (int i = 1; i <= n; ++i) {// int inv_len_i = inv(R[i] - L[i]);// yzh.query(ll[i] + 1, rr[i] - 1, ll[i] + 1, rr[i] - 1);// ans = add(ans, yzh.tr.sum[4]);// ans = sub(ans, mul(inv_len_i, sub(mul(yzh.tr.sum[4], R[i]), yzh.tr.sum[1])));// ans = sub(ans, mul(mul(inv2, inv_len_i), yzh.tr.sum[0]));// // if (i == 3) {// // for (int j = 0; j < 5; ++j)// // printf("sum[%d] = %d\n", j, yzh.tr.sum[j]);// // }// if (rr[i] != V) {// yzh.query(ll[i] + 1, rr[i] - 1, rr[i] + 1, V);// int TTT = 0;// TTT = sub(TTT, inv(mul(inv(mul(R[i], R[i])), yzh.tr.sum[0])));// TTT = add(TTT, mul(mul(2, R[i]), yzh.tr.sum[3]));// TTT = sub(TTT, yzh.tr.sum[2]);// TTT = mul(TTT, mul(inv2, inv_len_i));// TTT = add(yzh.tr.sum[4], TTT);// // printf(">>> %d\n", TTT);// ans = add(ans, TTT);// // if (i == 2) {// // printf(">>> %d\n", yzh.tr.sum[4]);// // printf(">>> %d\n", inv(mul(inv(mul(R[i], R[i])), yzh.tr.sum[0])));// // printf(">>> %d\n", mul(mul(2, R[i]), yzh.tr.sum[3]));// // printf(">>> %d\n", yzh.tr.sum[2]);// // }// // ans = add(ans, yzh.tr.sum[4]);// // ans = sub(ans, inv(mul(inv(mul(R[i], R[i])), yzh.tr.sum[0])));// // ans = add(ans, mul(mul(2, R[i]), yzh.tr.sum[3]));// // ans = sub(ans, yzh.tr.sum[2]);// }// yzh.modify(ll[i], rr[i], L[i], R[i]);// // printf("%d: ans = %d\n", i, ans);// }// printf("%d", ans);fprintf(stderr, "Time used %.2lfs.\n", clock() * 1. / CLOCKS_PER_SEC);}
}
#endifchar ED;signed main() {fprintf(stderr, "Memory: %.2lf MB\n", (&ED - &ST) / 1024.0 / 1024.0);#ifndef XuYuemingfreopen("rng.in", "r", stdin);freopen("rng.out", "w", stdout);#endiffread(buf, 1, MAX, stdin);read(n);for (register int i = 1; i <= n; ++i)read(L[i]), read(R[i]);// scanf("%d", &n);// for (int i = 1; i <= n; ++i)// scanf("%d%d", &L[i], &R[i]);#ifndef XuYueming// if (pts60::check()) return pts60::solve(), 0;if (l0::check()) return l0::solve(), 0;#endifreturn yzh520::solve(), 0;
}/*
3
4 9
2 5
1 4
*//*
2
2 3
3 6
*//*
2
7 8
7 9
*//*
2
4 10
3 6
*//*
2
8 10
2 8
*//*
3
8 10
7 9
0 8
*//*
3
0 5
4 9
0 10
*/
#include <cstdio>
#include <iostream>
#include <functional>
#include <algorithm>
#include <cstring>
#include <cassert>
#include <limits>const int N = 100010;namespace Bit_Tree_Class {template <typename T>static constexpr inline T lowbit(T x) {return x & -x;}template <int f>class Jumper {public:static constexpr inline int nxt(int x) { return x + f * lowbit(x); }static constexpr inline int pre(int x) { return x - f * lowbit(x); }};using prefix = Jumper< 1>;using suffix = Jumper<-1>;template <typename T, typename = void>struct hasNxt : std::false_type {};template <typename T>struct hasNxt<T, std::void_t<decltype(std::declval<T>().nxt)>> : std::true_type {};template <typename T, typename = void>struct hasPre : std::false_type {};template <typename T>struct hasPre<T, std::void_t<decltype(std::declval<T>().pre)>> : std::true_type {};template <typename T>auto gen_empty_v = [] () -> T { return T {}; };template <typename T = int, typename jmp = prefix, auto upd = std::plus<T>{}, auto gen_empty_v_func = gen_empty_v<T>, size_t N = N>class Bit_Tree {static_assert(std::is_convertible_v<decltype(upd), std::function<T(T, T)>>,"update function must work with T and T and returns T.");static_assert(hasNxt<jmp>::value, "jumper must have nxt function.");static_assert(hasPre<jmp>::value, "jumper must have pre function.");static_assert(std::conjunction_v<std::is_convertible<decltype(jmp::nxt), std::function<int(int)>>,std::is_convertible<decltype(jmp::pre), std::function<int(int)>>>,"jump functions must work with int and returns int.");static_assert(std::is_convertible_v<decltype(gen_empty_v_func), std::function<T()>>,"gen empty v func must return an empty value of T.");public:constexpr Bit_Tree() = default;constexpr explicit Bit_Tree(int _n): n(_n) { clear(); }constexpr inline void init(int _n) { n = _n, clear(); }constexpr inline void clear() { std::fill(tree + 1, tree + n + 1, empty_v); }constexpr inline void modify(int p, T v) {for (int i = p; 1 <= i && i <= n; i = jmp::nxt(i))tree[i] = upd(tree[i], v);}constexpr inline T query(int p) const {T res = empty_v;for (int i = p; 1 <= i && i <= n; i = jmp::pre(i))res = upd(res, tree[i]);return res;}protected:int n;T tree[N];static constexpr T empty_v = gen_empty_v_func();};template <typename T = int, typename jmp = prefix, auto upd = std::plus<T>{}, auto del = std::minus<T>{},auto gen_empty_v_func = gen_empty_v<T>, size_t N = N>class RQuery_Bit_Tree: public Bit_Tree<T, jmp, upd, gen_empty_v_func, N> {};template <typename T, auto upd, auto del, auto gen_empty_v_func, size_t N>class RQuery_Bit_Tree<T, prefix, upd, del, gen_empty_v_func, N>:public Bit_Tree<T, prefix, upd, gen_empty_v_func, N> {static_assert(std::is_convertible_v<decltype(del), std::function<T(T, T)>>,"del function must work with T and T and returns T.");public:constexpr inline T query(int l, int r) const {using __base = Bit_Tree<T, prefix, upd, gen_empty_v_func, N>;if (l > r) return __base::empty_v;return del(__base::query(r), __base::query(l - 1));}};template <typename T, auto upd, auto del, auto gen_empty_v_func, size_t N>class RQuery_Bit_Tree<T, suffix, upd, del, gen_empty_v_func, N>:public Bit_Tree<T, suffix, upd, gen_empty_v_func, N> {static_assert(std::is_convertible_v<decltype(del), std::function<T(T, T)>>,"del function must work with T and T and returns T.");public:constexpr inline T query(int l, int r) const {using __base = Bit_Tree<T, suffix, upd, gen_empty_v_func, N>;if (l > r) return __base::empty_v;return del(__base::query(l), __base::query(r + 1));}};
}namespace Mod_Int_Class {template <typename T, typename _Tp>constexpr bool in_range(_Tp val) {return std::numeric_limits<T>::min() <= val && val <= std::numeric_limits<T>::max();}template <auto mod = 998244353, typename T = int, typename S = long long>class Mod_Int {static_assert(in_range<T>(mod), "mod must in the range of type T.");static_assert(std::is_integral<T>::value, "type T must be an integer.");static_assert(std::is_integral<S>::value, "type S must be an integer.");public:constexpr Mod_Int() noexcept = default;template <typename _Tp, typename = std::enable_if_t<std::is_integral<_Tp>::value>>constexpr Mod_Int(_Tp v) noexcept: val(0) {if (0 <= v && v < mod) val = v;else val = (v % mod + mod) % mod;}constexpr T const& raw() const {return this -> val;}static constexpr inline T add(T a, T b) {return a + b >= mod ? a + b - mod : a + b;}static constexpr inline T sub(T a, T b) {return a < b ? a - b + mod : a - b;}static constexpr inline T mul(T a, T b) {return static_cast<S>(a) * b % mod;}static constexpr inline T& toadd(T& a, T b) {return a = add(a, b);}static constexpr inline T& tosub(T& a, T b) {return a = sub(a, b);}static constexpr inline T& tomul(T& a, T b) {return a = mul(a, b);}template <typename _Tp, typename = std::enable_if_t<std::is_integral<_Tp>::value>>static constexpr inline T pow(T a, _Tp p) {T res = 1;for (; p; p >>= 1, tomul(a, a))if (p & 1) tomul(res, a);return res;}template <typename _Tp, typename = std::enable_if_t<std::is_integral<_Tp>::value>>static constexpr inline bool is_prime(_Tp val) {if (val < 2) return false;for (_Tp i = 2; i * i <= val; ++i)if (val % i == 0)return false;return true;}template <typename = std::enable_if_t<is_prime(mod)>>static constexpr inline T inv(T a) {assert(a != 0);return pow(a, mod - 2);}constexpr Mod_Int& operator + () const {return *this;}constexpr Mod_Int operator - () const {return sub(0, val);}constexpr friend inline Mod_Int operator + (Mod_Int a, Mod_Int b) {return add(a.val, b.val);}constexpr friend inline Mod_Int operator - (Mod_Int a, Mod_Int b) {return sub(a.val, b.val);}constexpr friend inline Mod_Int operator * (Mod_Int a, Mod_Int b) {return mul(a.val, b.val);}constexpr friend inline Mod_Int operator / (Mod_Int a, Mod_Int b) {return mul(a.val, inv(b.val));}template <typename _Tp, typename = std::enable_if_t<std::is_integral<_Tp>::value>>constexpr friend inline Mod_Int operator ^ (Mod_Int a, _Tp p) {return pow(a, p);}constexpr friend inline Mod_Int& operator += (Mod_Int& a, Mod_Int b) {return a = add(a.val, b.val);}constexpr friend inline Mod_Int& operator -= (Mod_Int& a, Mod_Int b) {return a = sub(a.val, b.val);}constexpr friend inline Mod_Int& operator *= (Mod_Int& a, Mod_Int b) {return a = mul(a.val, b.val);}constexpr friend inline Mod_Int& operator /= (Mod_Int& a, Mod_Int b) {return a = mul(a.val, inv(b.val));}template <typename _Tp, typename = std::enable_if_t<std::is_integral<_Tp>::value>>constexpr friend inline Mod_Int& operator ^= (Mod_Int& a, _Tp p) {return a = pow(a.val, p);}constexpr friend inline bool operator == (Mod_Int a, Mod_Int b) {return a.val == b.val;}constexpr friend inline bool operator != (Mod_Int a, Mod_Int b) {return a.val != b.val;}protected:T val;};using mint = Mod_Int<>;constexpr mint operator ""_m (unsigned long long x) {return mint(x);}constexpr mint operator ""_mod (unsigned long long x) {return mint(x);}
}using namespace std;
using namespace Mod_Int_Class;
using namespace Bit_Tree_Class;using tree_t = RQuery_Bit_Tree<mint, prefix, std::plus<mint>{}, std::minus<mint>{}, gen_empty_v<mint>, N << 1>;tree_t yzh[3];constexpr mint inv2 = 1_mod / 2;int n, L[N], R[N], ll[N], rr[N];
int real[N << 1], V;
mint ans;signed main() {#ifndef XuYuemingfreopen("rng.in", "r", stdin);freopen("rng.out", "w", stdout);#endifscanf("%d", &n);for (int i = 1; i <= n; ++i) {scanf("%d%d", &L[i], &R[i]);real[++V] = L[i], real[++V] = R[i];}sort(real + 1, real + V + 1);V = unique(real + 1, real + V + 1) - real - 1;for (int i: {0, 1, 2}) yzh[i].init(V);for (int i = 1; i <= n; ++i) {ll[i] = lower_bound(real + 1, real + V + 1, L[i]) - real;rr[i] = lower_bound(real + 1, real + V + 1, R[i]) - real;}for (int i = n; i >= 1; --i) {mint inv_len = 1_mod / (R[i] - L[i]);auto calc = [&inv_len] (int x, int p) -> mint {mint res = 0;res += yzh[0].query(p, V) * x * x * inv2;res += yzh[1].query(1, p - 1) * x;res -= yzh[2].query(1, p - 1) * inv2;return res * inv_len;};ans += calc(R[i], rr[i]);ans -= calc(L[i], ll[i]);static auto update = [] (int x, int p, mint val) -> void {yzh[0].modify(p, val);yzh[1].modify(p, val * x);yzh[2].modify(p, val * x * x);};update(R[i], rr[i], inv_len);update(L[i], ll[i], -inv_len);}printf("%d", ans.raw());return 0;
}
