PDF文档公众号回复关键字:20240926

1 2019 CSP-J 题目4 加工零件
[题目描述]
凯凯的工厂正在有条不紊地生产一种神奇的零件,神奇的零件的生产过程自然也很神奇。工厂里有 n位工人,工人们从 1∼n 编号。某些工人之间存在双向的零件传送带。保证每两名工人之间最多只存在一条传送带
如果 x号工人想生产一个被加工到第 L (L>1)阶段的零件,则所有与 x号工人有传送带直接相连的工人,都需要生产一个被加工到第 L−1 阶段的零件(但 x号工人自己无需生产第 L−1 阶段的零件)
如果 x 号工人想生产一个被加工到第 1 阶段的零件,则所有与 x 号工人有传送带直接相连的工人,都需要为 x 号工人提供一个原材料
轩轩是 1 号工人。现在给出 q张工单,第 i张工单表示编号为 ai的工人想生产一个第 Li 阶段的零件。轩轩想知道对于每张工单,他是否需要给别人提供原材料。他知道聪明的你一定可以帮他计算出来
[输入格式]
第一行三个正整数 n,m 和 q,分别表示工人的数目、传送带的数目和工单的数目
接下来 m行,每行两个正整数 u 和 v,表示编号为 u 和 v 的工人之间存在一条零件传输带。保证 u≠v
接下来 q 行,每行两个正整数 a 和 L,表示编号为 a 的工人想生产一个第 L 阶段的零件
[输出格式]
共 q 行,每行一个字符串 Yes 或者 No
如果按照第 i 张工单生产,需要编号为 1 的轩轩提供原材料,则在第 i 行输出 Yes;否则在第 i 行输出 No。注意输出不含引号
[输入输出样例]
输入 #1
3 2 6
1 2
2 3
1 1
2 1
3 1
1 2
2 2
3 2
输出 #1
No
Yes
No
Yes
No
Yes
输入 #2
5 5 5
1 2
2 3
3 4
4 5
1 5
1 1
1 2
1 3
1 4
1 5
输出 #2
No
Yes
No
Yes
Yes
说明/提示
样例 1 说明
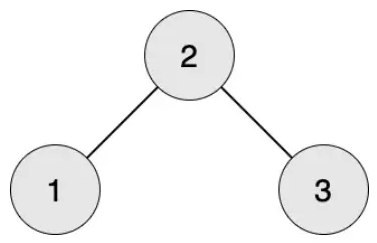
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 2 的工人想生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料。
编号为 3 的工人想生产第 1 阶段的零件,需要编号为 2 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零 件,需要编号为 1 和 3 的工人提供原材料。
编号为 2 的工人想生产第 2 阶段的零件,需要编号为 1 和 3 的工人生产第 1 阶段的零件,他/她们都需要编号为 2 的工人提供原材料。
编号为 3 的工人想生产第 2 阶段的零件,需要编号为 2 的工人生产第 1 阶段的零件,需要编号为 1 和 3 的工人提供原材料
样例 2 说明
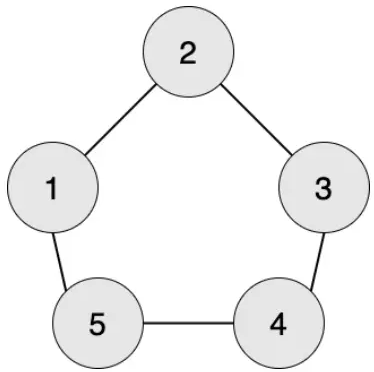
编号为 1 的工人想生产第 1 阶段的零件,需要编号为 2 和 5 的工人提供原材料。
编号为 1 的工人想生产第 2 阶段的零件,需要编号为 2 和 5 的工人生产第 1 阶段的零件,需要编号为 1,3,4 的工人提供原材料。
编号为 1 的工人想生产第 3 阶段的零件,需要编号为 2 和 5 的工人生产第 2 阶段的零件,需要编号为 1,3,4 的工人生产第 1 阶段的零件,需要编号为 2,3,4,5 的工人提供原材料。
编号为 1 的工人想生产第 4 阶段的零件,需要编号为 2 和 5 的工人生产第 3 阶段的零件,需要编号为 1,3,4 的工人生产第 2 阶段的零件,需要编号为 2,3,4,5 的工人生产第 1 阶段的零件,需要全部工人提供原材料。
编号为 1 的工人想生产第 5 阶段的零件,需要编号为 2 和 5 的工人生产第 4 阶段的零件,需要编号为 1,3,4 的工人生产第 3 阶段的零件,需要编号为 2,3,4,5 的工人生产第 2 阶段的零件,需要全部工人生产第 1 阶段的零件,需要全部工人提供原材料
2 相关知识点
1) 位运算
整数映射0或1
#include<bits/stdc++.h>
using namespace std;int n;
/*对于整数n,进行如下操作 n&1,如果是偶数结果为0,如果为奇数结果为12&1=03&1=1
*/
int main(){n=2;int op1 = n&1; cout<<"op1:"<<op1<<endl;n=3;int op2 = n&1;cout<<"op2:"<<op2<<endl;return 0;
}
/*
op1:0
op2:1
*/
2) 结构体
初始化列表构造
#include<bits/stdc++.h>
using namespace std;
/*C++提供了给成员变量初始化并赋值的方式,这就是初始化列表。在构造函数的()后,{}之前写,格式是冒号+成员名(初始值),对与自定义类型则是调用它的构造函数初始化
*/
struct xy{int x;int y;xy(int x,int y):x(x),y(y){}//初始化列表方式对成员变量进行初始化
};int main(){xy xy1=xy(1,2);//通过构造函数传入参数给成员变量x,y cout<<xy1.x<<" "<<xy1.y;//输出成员变量x和y return 0;
}
3) 动态数组
#include<bits/stdc++.h>
using namespace std;vector<int> a(11,1);//声明数组a并赋值1
vector<int> b(11);//声明数组a,默认赋值0
int main(){a.push_back(2);//在a最后一个元素后面追加2 a.push_back(4);//在a最后一个元素后面追加4 for(int i=0;i<a.size();i++){//输出a数组中每个元素 cout <<a[i]<< ' ';}cout<<endl;for(int i=0;i<b.size();i++){//输出b数组中每个元素cout <<b[i]<< ' ';C++}return 0;
}
/*
输出
1 1 1 1 1 1 1 1 1 1 1 2 4
0 0 0 0 0 0 0 0 0 0 0
*/
vector二维动态数组
#include<bits/stdc++.h>
using namespace std;
vector<int> v[2];//定义10行,每行是一个vector数组
/*vector定义二维数组,行固定列可变示例定义2行,第1行2列,第2行3列
*/
int main(){//第1行第1列放入2 v[0].push_back(2);//第1行第2列放入3 v[0].push_back(3);//第2行第1列放入4 v[1].push_back(4);//第2行第2列放入5v[1].push_back(5);//第2行第3列放入6 v[1].push_back(6);for(int i=0;i<=1;i++){for(int j=0;j<v[i].size();j++){cout<<v[i][j]<<" ";}cout<<endl;}return 0;
}
/*
2 3
4 5 6
*/
4) 队列
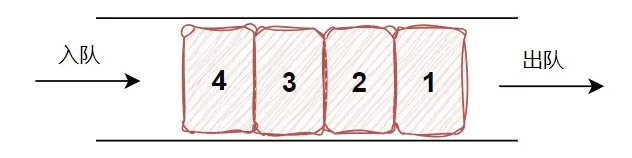
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(head)进行删除操作,而在表的后端(tail)进行插入操作
队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头
队列可以理解成我们平时的排队,先进入的先出去
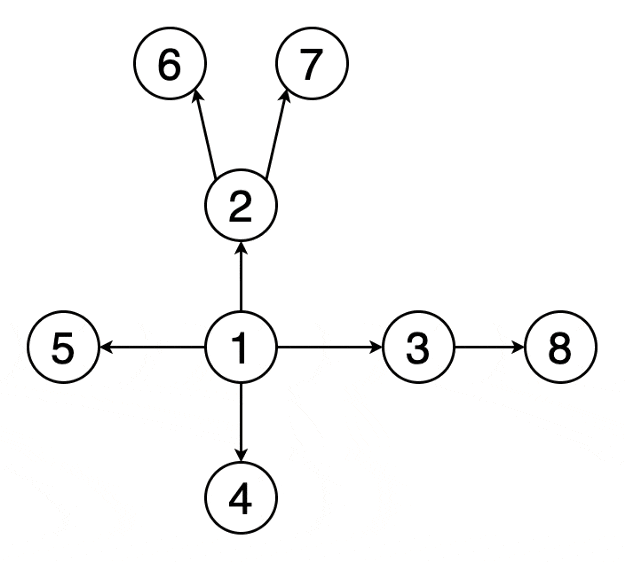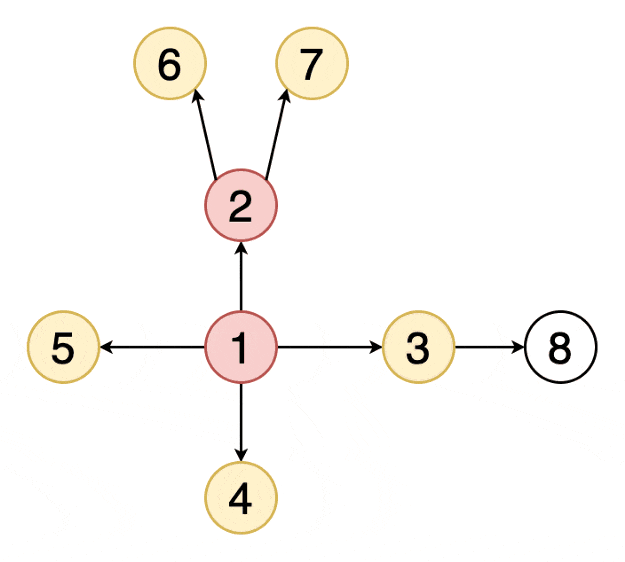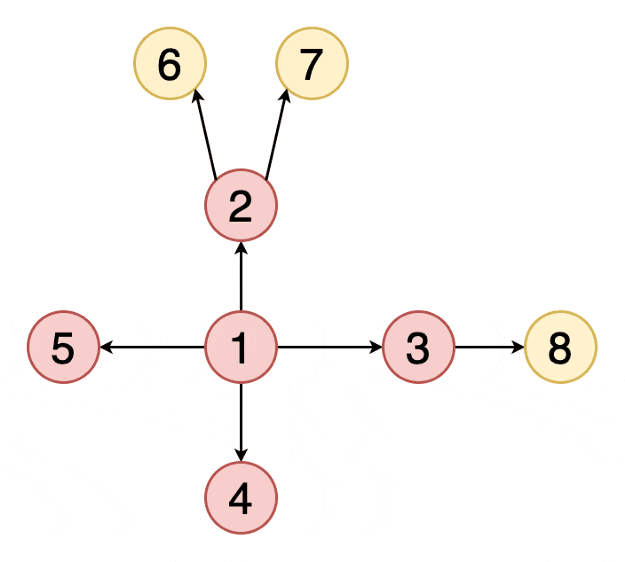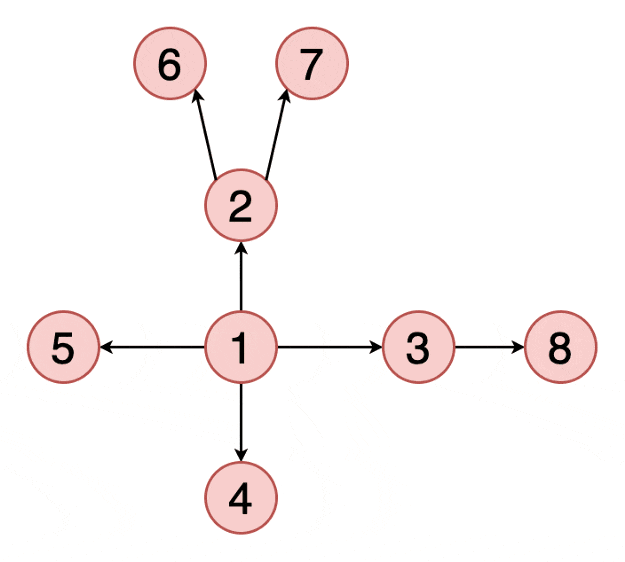
5) 宽度优先搜索 BFS
(BFS, Breadth First Search)是一个针对图和树的遍历算法。发明于上世纪50年代末60年代初,最初用于解决迷宫最短路径和网络路由等问题
是从根结点开始沿着树的宽度搜索遍历,将离根节点最近的节点先遍历出来,在继续深入遍历
实现DFS时,通常使用队列数据结构实现
3 思路分析
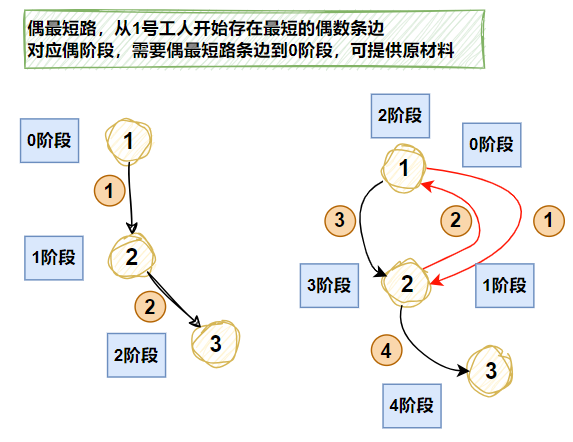
A工人,从0阶段到某一阶段,如下到2阶段,走2步可以提供原材料
A工人,从0阶段到某一阶段,如下到2阶段,走3步则不可以提供原材料
A工人,从0阶段到某一阶段,如下到2阶段,走4步则可以提供原材料(可以在1~2之间走2次)
由上可知,到偶数阶段零件,从原材料可以通过偶数步生产
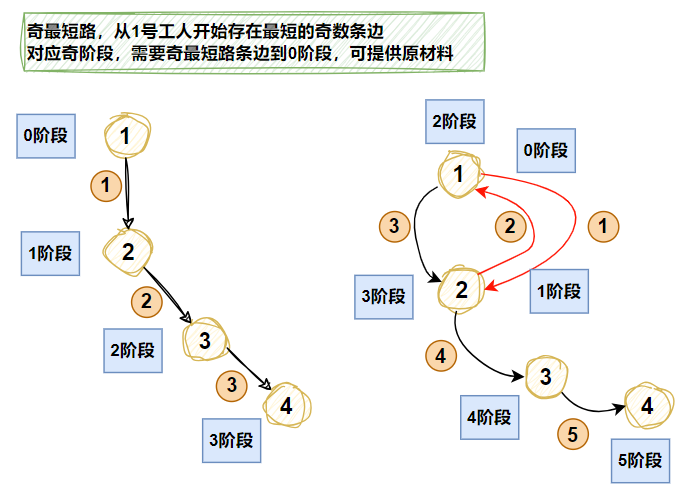
A工人,从0阶段到某一阶段,如下到3阶段,走3步可以提供原材料
A工人,从0阶段到某一阶段,如下到3阶段,走4步则不可以提供原材料
A工人,从0阶段到某一阶段,如下到3阶段,走5步则可以提供原材料(可以在1~2之间走2次)
由上可知,到奇数阶段零件,从原材料可以通过奇数步生产
综上,上面问题可以转换成分2种情况求最短路问题
需要奇数步生产,求奇数步的最短路
需要偶数步生产,求偶数步最短路
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,m,q;//n表示工人数,m表示传送带数,q表示工单数
vector<int> to[maxn];//定义vector数组,maxn个vector,存放传送带
/*从1号工人到当前编号工人的奇最短路或偶最短路dis[3][0] 表示1号工人到3号工人的偶最短路 dis[3][1] 表示1号工人到3号工人的奇最短路
*/
int dis[maxn][2];
struct node{//结构体 int id;//工人编号 int dis;//从1号工人到当前工人的距离 node(int a=0,int b=0):id(a),dis(b){};//初始化列表构造node
};
queue<node> Q;//bfs使用队列 队列存储node结构体
/*通过bfs计算1号工人到其他工人的最短路如果到某工人距离是偶数,存储偶最短路 dis[i][0]如果到某工人距离是奇数,存储奇最短路 dis[i][1]
*/
void bfs(){for(int i=1;i<=n;i++){//初始化1号工人到所有工人奇偶最短路为-1,没有最短路 dis[i][0]=dis[i][1]=-1;}dis[1][0]=0;//从1号工人开始 Q.push(node(1,0));//1号工人放入队列 while(!Q.empty()){node now=Q.front();Q.pop();//取出队首 当前工人 int u=now.id;//当前工人编号 for(int i=0;i<to[u].size();i++){//和当前工人相邻的其他工人 int v=to[u][i];int x=now.dis+1;//当前距离+1 int op=x&1;//计算距离奇偶数 ,如果偶数为0,奇数为1 if(dis[v][op]!=-1) continue;//如果已经计算过距离,说明前面计算更短,不走此路 dis[v][op]=x;//计算最短路赋值 Q.push(node(v,x));//放入队列,计算此工人可连接工人的最短路 }}
}
int main(){scanf("%d%d%d",&n,&m,&q);//输入工人数 传送带数 工单数 for(int i=1,u,v;i<=m;i++){//输入对应的传送带 scanf("%d%d",&u,&v);to[u].push_back(v);to[v].push_back(u);}bfs();//宽搜计算1号工人到所有工人的奇偶最短路 存储到dis 数组 for(int i=1,a,L,op;i<=q;i++){//循环到dis数组中找对应的最短路 scanf("%d%d",&a,&L);//a号工人 生产L阶段零件 op=L&1;//判断L阶段的奇偶 偶数到dis[][0]找最短路,奇数到dis[][1]找最短路 if(dis[a][op]==-1) printf("No\n");//如果为-1没用最短路 无法提供原材料 else if(dis[a][op]>L) printf("No\n");//如果最短路大于L,无法达到,无法提供原材料 else printf("Yes\n");//其他可以提供原材料 }return 0;
}