很好一题目,使我的最小圆覆盖旋转。
先假设 \(p = 1\)。这是最简单的情况。这个时候我们就得到了一个裸的最小圆覆盖。
当 \(p \not= 1\),但是 \(a = 0\) 的时候。圆就变成了对称轴与坐标轴平行的椭圆,运用高中知识仿射一下,又回到了最小圆覆盖。
在一般的情况下,我们先通过坐标的旋转回到第二种情况,再进行仿射,又是最小圆覆盖。
目前为止实际上这个题目已经做完了。如果你还不会做,那么你一定遇到了下面这个问题:
什么是最小圆覆盖
模板题传送门
最小圆覆盖问题是指:在二维平面上有一堆点,求一个最小半径的圆,能够将所有点全部都包住。
为解决这个问题,我们首先引入三个性质:
性质 1:最小覆盖圆是唯一的
证明:假设存在两个圆,它们的都是符合要求的最小圆。设它们的半径为 \(r\)。那么所有的点就必定落在下图中的蓝色区域:
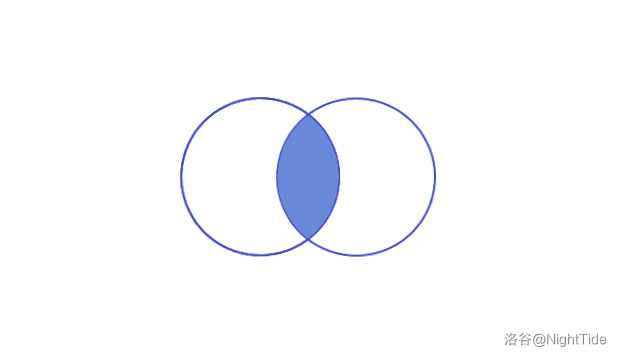
而我们以两圆的两个交点为直径再做一个圆(如下图中紫色圆),显然它包含了该区域中的任意点,并且其直径为原本的两圆的一条弦,必然小于原本的两圆的直径:
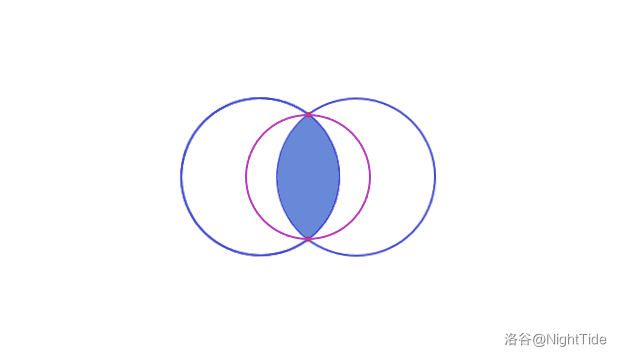
那么,蓝色圆不为最小圆,与假设冲突。
性质 2:对于一个点集,其最小覆盖圆只为两种情况之一:1. 圆由该点集内三个或者三个以上的点共同确定;2. 该点集内的两个点确定圆的直径
证明:记满足该两种情况为命题 \(p\),是某个点集的最小覆盖圆为命题 \(q\)。
假如点集内没有点落在圆上,那么显然圆保持圆心不变,一直收缩。必然能够到某一状态,使得至少一个点落在圆上。
假如点集内只有一个点落在圆上,保持该点始终在圆上收缩半径,也必定在某一状态,使得另一点落在圆上。
假如点集内有两点落在圆上,但两点不构成直径。让圆心在两点确定的线段的中垂线上移动,必然存在某一状态,使得除了这两点以外的某一点也落在圆上
综上,\(\neg p\Rightarrow \neg q\),即 \(p \Rightarrow q\)。
对于一个只有两个点的点集,显然条件二为最小覆盖圆。
对于一个等边三角形的三个顶点构成的点集,显然条件一为最小覆盖圆。
综上,\(\exists\) 圆 \(O\) 满足 \(p\),使得 \(q\) 成立。
性质 3:对于一个已知点集 \(S\),已知其最小覆盖圆为圆 \(O_1\)。向点集内新增一点 \(P\),若 \(P\) 在圆外,则新点集的最小覆盖圆过点 \(P\)。
证明:对于一个新圆 \(O_2\),其包含了点集 \(S\) 中的所有点和 \(P\),且 \(P\) 在圆 \(O_2\) 内。
若 \(O_2\) 上只有两个点。 \(S\) 中任意两点间的距离必然小于圆 \(O_1\) 的直径,那么这两点不可能构成 \(O_2\) 的直径,与性质 2 冲突。
若 \(O_2\) 上有三个或三个以上的点,如图(深蓝色为 \(O_1\),天青色为 \(O_2\)),\(S\) 中的点必然被包含在浅蓝色区域内:
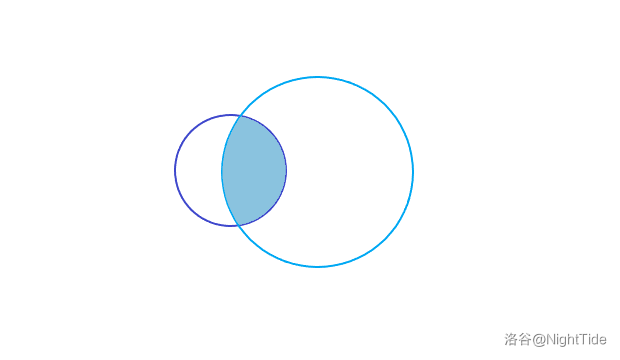
类似于性质 1 的证明,圆 \(O_1\) 不为点集 \(S\) 的最小覆盖圆,与题设冲突。
于是得证。
引入这三个性质之后,我们就可以得到一个玄而又玄的算法:随机增量算法。
首先将所有的点随机化(随机化的作用在之后),记该点集为 \(S\),\(S_i\) 代表点集中的第 \(i\) 个点。
接着初始化一个半径为 \(0\),圆心为 \(S_1\) 的圆。
接着遍历所有点,将当前枚举到的点丢入已知点集中,并维护一个新的最小覆盖圆,以此类推。
问题在于,当我们已知前 \(i- 1\) 个点的最小覆盖圆时,如何确定加入第 \(i\) 个点后的最小覆盖圆。
若 \(S_i\) 在圆内,那么直接继续循环。
若 \(S_i\) 在圆外,由性质 3,新的最小覆盖圆过点 \(S_i\)。此时我们已知圆上一点,不足以确定一个圆。
于是我们又初始化一个半径为 \(0\),圆心为 \(S_i\) 的圆。从 \(i - 1\) 开始向前枚举 \(j\),此时性质 3 依然适用。
若 \(S_j\) 在圆内,那么直接继续循环。
若 \(S_j\) 在圆外,由性质 3,新的最小覆盖圆过点 \(S_j\)。此时我们已知圆上两点,依旧不够。
于是我们又初始化一个以 \(S_i\) 和 \(S_j\) 为直径的圆,从 \(1 \sim j - 1\) 枚举 \(k\),依旧利用性质 \(3\)。
若 \(S_k\) 在圆内,那么直接继续循环。
若 \(S_k\) 在圆外,由性质 3,新的最小覆盖圆过点 \(S_k\)。此时三点确定一个圆。
当 \(k\) 循环结束时,我们就得到了加入第 \(i\) 个点后的最小覆盖圆。
核心代码如下:
random_shuffle(p + 1, p + n + 1);// 随机化数组
// 结构体 (coor){x 坐标,y 坐标},数组 p 是该类型
// 结构体 (circle){圆心,半径}
c = (circle){p[1], 0};
for(int i = 2; i <= n; i++){// double_cmp(double a, double b):比较两个浮点数 a 和 b 的大小if(double_cmp(c.r, get_dis(c.o, p[i])) == -1){c = (circle){p[i], 0};for(int j = 1; j < i; j++){if(double_cmp(c.r, get_dis(c.o, p[j])) == -1){// get_dis(coor a, coor b):两点之间距离c = (circle){(p[i] + p[j]) / 2, get_dis(p[i], p[j]) / 2};for(int k = 1; k < j; k++){// get_circle(coor a, coor b, coor c):三点确定圆if(double_cmp(c.r, get_dis(c.o, p[k])) == -1) c = get_circle(p[i], p[j], p[k]);}}}}
}
好现在有人问,这玩意儿不是 \(O(n^3)\) 的吗?
这只是理论最坏时间复杂度。然而实际上,每次在进入下一层循环时,都会判定一次当前点是否在当前圆外。可以证明,当数据随机时,我们只有 \(\frac{3}{n}\) 的概率遇到一个在圆外的点。这也是随机化处理的原因。在随机化处理后,时间复杂度就变为了 \(O(n\times\frac{3}{n}\times n\times\frac{3}{n}\times n)\),即 \(O(n)\)。
完整代码如下
#include<bits/stdc++.h>
#define MAXN 100010
#define eps 1e-9
#define pi acos(-1)
using namespace std;
struct coor{ double x, y; };
struct circle{ coor o; double r; };
coor operator + (coor a, coor b){ return (coor){a.x + b.x, a.y + b.y}; }
coor operator - (coor a, coor b){ return (coor){a.x - b.x, a.y - b.y}; }
coor operator * (coor a, double b){ return (coor){a.x * b, a.y * b}; }
coor operator / (coor a, double b){ return (coor){a.x / b, a.y / b}; }
double operator * (coor a, coor b){ return a.x * b.y - a.y * b.x; }
int double_cmp(double a, double b){if(fabs(a - b) < eps) return 0;if(a < b) return -1;return 1;
}
// 向量旋转 b,单位为弧度
coor rotate(coor a, double b){ return (coor){a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)}; }
// 两点间距离
double get_dis(coor a, coor b){double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}
// 两直线交点,p 和 v,q 和 w 分别确定两条直线
coor inter_section(coor p, coor v, coor q, coor w){coor u = p - q;double t = (w * u) / (v * w);return p + v * t;
}
// 求中垂线,用两点表示一条直线
pair<coor, coor> bisector(coor a, coor b){coor p = (a + b) / 2;coor q = rotate(b - a, pi/2);return make_pair(p, q);
}
// 三点定圆
circle get_circle(coor a, coor b, coor c){pair<coor, coor> x = bisector(a, b), y = bisector(a, c);coor o = inter_section(x.first, x.second, y.first, y.second);double r = get_dis(o, a);return (circle){o, r};
}
int n;
circle c;
coor p[MAXN];
int main(){scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%lf%lf",&p[i].x,&p[i].y);random_shuffle(p + 1, p + n + 1);c = (circle){p[1], 0};for(int i = 2; i <= n; i++){if(double_cmp(c.r, get_dis(c.o, p[i])) == -1){c = (circle){p[i], 0};for(int j = 1; j < i; j++){if(double_cmp(c.r, get_dis(c.o, p[j])) == -1){c = (circle){(p[i] + p[j]) / 2, get_dis(p[i], p[j]) / 2};for(int k = 1; k < j; k++){if(double_cmp(c.r, get_dis(c.o, p[k])) == -1) c = get_circle(p[i], p[j], p[k]);}}}}}printf("%.10lf\n",c.r);printf("%.10f %.10f\n",c.o.x, c.o.y);
}
回到本题
好的以上是最小圆覆盖,根据一开始的思路,我们很容易就能够将上面那份板子改为本题的答案。
#include<bits/stdc++.h>
#define MAXN 100010
#define eps 1e-9
#define pi acos(-1)
using namespace std;
struct coor{ double x, y; };
struct circle{ coor o; double r; };
coor operator + (coor a, coor b){ return (coor){a.x + b.x, a.y + b.y}; }
coor operator - (coor a, coor b){ return (coor){a.x - b.x, a.y - b.y}; }
coor operator * (coor a, double b){ return (coor){a.x * b, a.y * b}; }
coor operator / (coor a, double b){ return (coor){a.x / b, a.y / b}; }
double operator * (coor a, coor b){ return a.x * b.y - a.y * b.x; }
int double_cmp(double a, double b){if(fabs(a - b) < eps) return 0;if(a < b) return -1;return 1;
}
coor rotate(coor a, double b){ return (coor){a.x * cos(b) + a.y * sin(b), -a.x * sin(b) + a.y * cos(b)}; }
double get_dis(coor a, coor b){double dx = a.x - b.x;double dy = a.y - b.y;return sqrt(dx * dx + dy * dy);
}
coor inter_section(coor p, coor v, coor q, coor w){coor u = p - q;double t = (w * u) / (v * w);return p + v * t;
}
pair<coor, coor> bisector(coor a, coor b){coor p = (a + b) / 2;coor q = rotate(b - a, pi/2);return make_pair(p, q);
}
circle get_circle(coor a, coor b, coor c){pair<coor, coor> x = bisector(a, b), y = bisector(a, c);coor o = inter_section(x.first, x.second, y.first, y.second);double r = get_dis(o, a);return (circle){o, r};
}
int n, a, t;
double b;
circle c;
coor p[MAXN];
int main(){scanf("%d", &n);for(int i = 1; i <= n; i++) scanf("%lf%lf",&p[i].x,&p[i].y);scanf("%d%d",&a,&t);b = a / 180.0 * pi;// 旋转for(int i = 1; i <= n; i++) p[i] = rotate(p[i], b);// 仿射for(int i = 1; i <= n; i++) p[i].x /= (double)t;random_shuffle(p + 1, p + n + 1);c = (circle){p[1], 0};for(int i = 2; i <= n; i++){if(double_cmp(c.r, get_dis(c.o, p[i])) == -1){c = (circle){p[i], 0};for(int j = 1; j < i; j++){if(double_cmp(c.r, get_dis(c.o, p[j])) == -1){c = (circle){(p[i] + p[j]) / 2, get_dis(p[i], p[j]) / 2};for(int k = 1; k < j; k++){if(double_cmp(c.r, get_dis(c.o, p[k])) == -1) c = get_circle(p[i], p[j], p[k]);}}}}}c.r *= 1000;c.r = round(c.r);c.r /= 1000;printf("%.3lf\n",c.r);
}