手把手教你建【货币】一题的网络流模型

现在已知如下问题，并告诉你这题可以用网络流来解决，你该怎么做，该怎么建出网络流的模型？

一些前提：

显然可以发现绝不可能走横向向左的边，但可能走竖向向上的边（如下图）

那么图其实就是这样的：问从 \(s\) 到 \(t\) 的最小花费

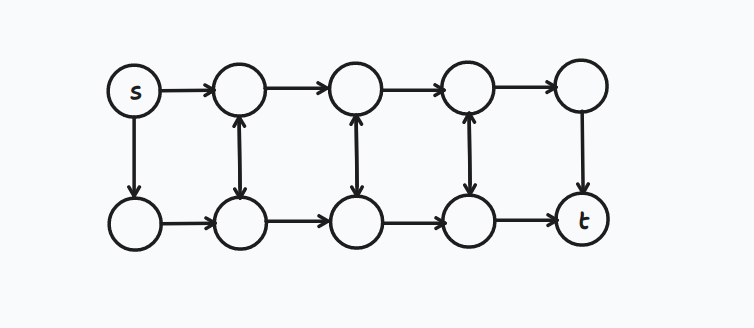
如果没有那 \(m\) 条限制，我们直接跑最短路就行了，加上这些限制，发现其实是个网络流模型，考虑如何建出网络流模型。

建模：

我们虚构出以下的模型以方便理解——很典的模型：对偶图！（具体什么是对偶图自行了解）

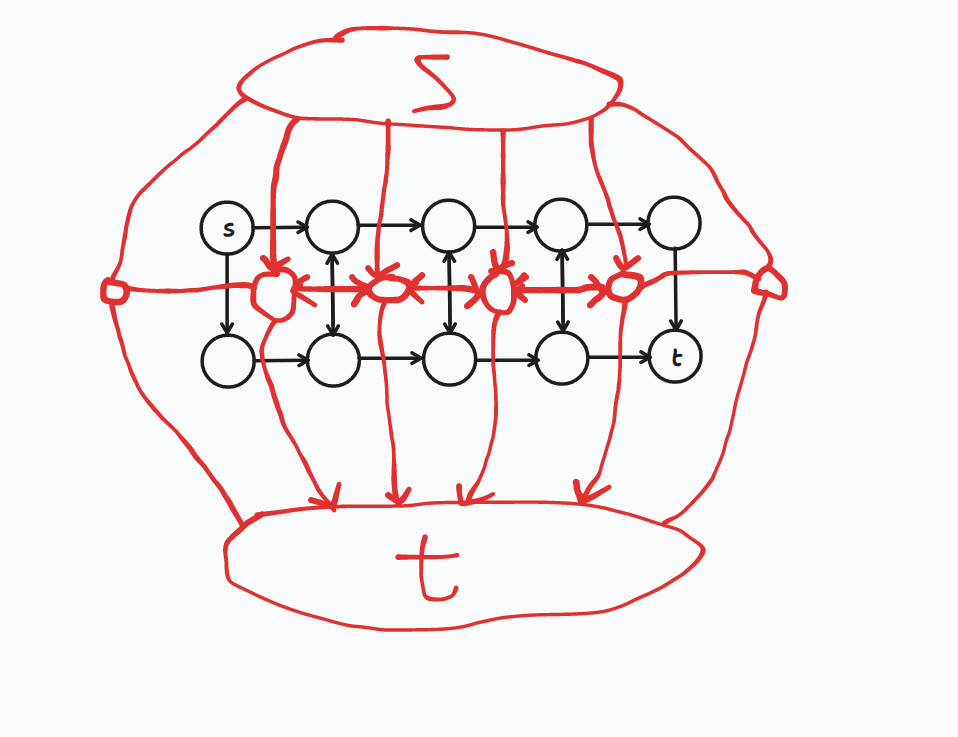
注：没方向的边是现在还不清楚该怎么建，稍后考虑。

每条红边（网络流上的边）的权值就是其交叉的黑边（实际的图）的权值

（好像个灯笼）现在实际上从 s 到 t 的最短花费其实就是 s 到 t 的红色连边构成的图的最小割了。

为什么？我们单独扣出来两个点证明一下：

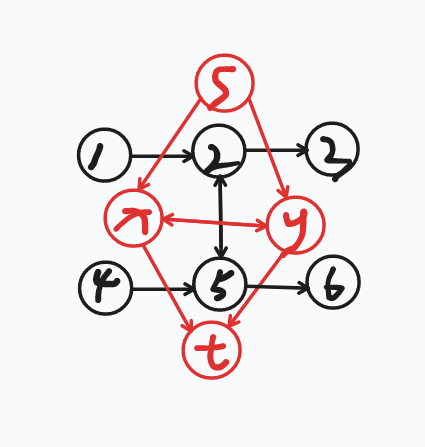
如上图，先不考虑横着的红边的话，根据最小割知识，我们知道在路径 \((s,x) 和 (x,t)\) 中必须要割掉一条且只割掉一条，同样，在 \((s,y) 和 (y, t)\) 中必须要割掉一条且只割掉一条，（必须割一条是为了满足没有增广路可以从 s 到 t ）；

为什么各只能割掉一条呢？

• 如果我们保证需要割 \((x,y)\) 这条边，则只会再割 \((s,y),(x,t)\)；不然无论是割 \((s,y),(s,x)\) 还是割 \((x,t),(y,t)\) 都会使得没有必要割 \((x,y)\)，与保证需要矛盾。
• 若割 \((y,x)\) 同理；
• 若既不割 \((x,y)\) 也不割 \((y,x)\)：
  • 如果保证需要割掉 \((x,t)\)，那么需要割 \((y,t)\) 时不用再割别的边了，这不用解释。那如果我们割 \((s,y)\) 呢，这样仍然有增广路 s->x->y->t，此时因为我们既不割 \((x,y)\) 也不割 \((y,t)\)，所以必须割掉 \((s,x)\)，此时会发现 \((s,x) 和 (x,y)\) 都割掉了，那么 \((x,t)\) 是没必要割的，矛盾！
  • 不割 \((x,t)\) 的话，同理。

对照实际的图，发现一样，如果走 1->2 这条边，一定不会走 4->5 这条边，走 2->3 一定不会走 5->6；

如果走了 2->5，那么要么是走 1->2->5->6，要么是走 4->5->2->3。

所以其实可以发现最小割就是原图中的最短路。

解决了以上问题，那么现在我们只需再解决 \(m\) 个限制条件 和 灯笼图中没有方向的红边（最左边和最右边点的边） 两个问题即可。

如何解决 \(m\) 个限制？

还是扣出两个点，（只扣模型点了），如果题目限制同时走 s->x 和 y->t （x 和 y 并不一定相邻）时，需要再增加大小为 \(c\) 的花费。（现在暂时当作没有虚线边）

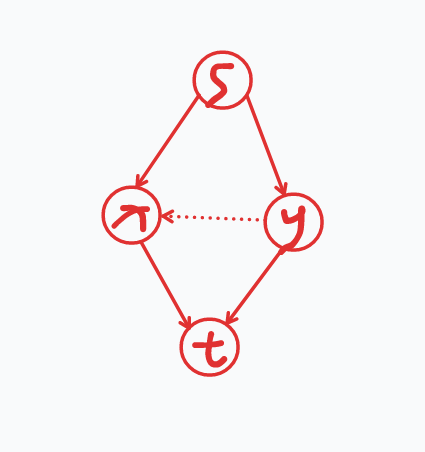
那么等同于我们需要考虑如何使得在既割 s->x 又割 y->t 的情况下，还需要再多割一条花费为 \(c\) 的边，我们再建一条从 y 到 x ，花费为 \(c\) 的边就解决了。（就是图中虚线边）。

显然割掉 s->x 和 y->t 后，还有一条增广路 s->y->x->t，所以必须再割掉 y->x，（上文已经证明出来此时不会再割 x->t 和 s->y ）。ok 了。

对于最左和最右那两个点的处理

现在把最右边那部分边拿出来，显然可以连成这样：

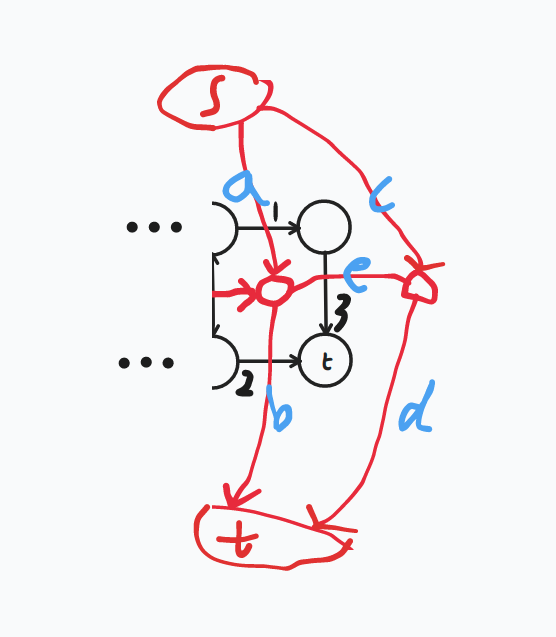
可以发现，在 1、2 边之间（显然这两条边只能走一个）如果我们走的是 2，则没什么事；但如果走的是 1 这条边，那么就一定要走 3 这条边。考虑在网络流上怎么解决？

意思就是需要在 a、b 之间选择割 a 这条边的时候，必须要再割掉 e 这条边。

其实把 d 权值附为 0，c 附为 inf，然后 e 从右边那个点连向左边那个即可，这样保证割 d 不割 c，此时若割 a，则还需要割掉 e 以使增广路 c-e-b 不再增广。

如下图：

\[e \]

\[@<--@ \]