1.世上有10种人
题目
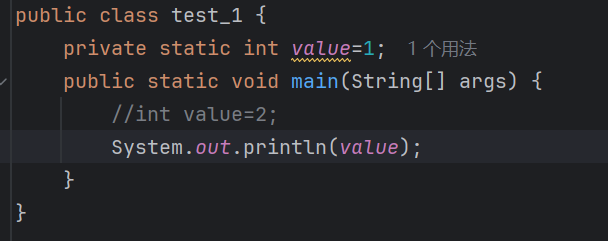
世上有10种人

代码
#include
using namespace std;
int main()
{cout<<2;return 0;
}
2.01切换
题目
01切换

题目分析
直接判断字符串最后一个字符是0还是1就好了
代码
#include
using namespace std;
int main()
{string str;cin>>str;int l = str.length();if (str[l - 1] == '0' ){str[l - 1] = '1' ;}else{str[l - 1] = '0' ;}cout << str;return 0;
}
3.数字换字母
数字换字母
题目

题目分析
1.使用映射表将字符串1与数字0~9进行对应
2.对字符串进行检测,碰到数字则进行对应切换
代码
#include
#include
#include using namespace std; int main()
{ // 读取字符串S string S; cin >> S; // 创建一个映射表,初始化为空字符,方便后续检查是否映射过 vector< char > mapping(10, '\0' ); // 填充映射表 for ( int i = 0; i < 10; ++i) { mapping[i] = S[i]; } // 读取字符串T string T; cin >> T; // 输出处理后的字符串 for ( char c : T) { // 检查c是否为数字字符('0'到'9') if (c >= '0' && c <= '9' ) { // 根据映射表找到对应的字母 cout << mapping[c - '0' ]; } else{ // 如果c不是数字,则直接输出 cout << c; } } return 0;
}
4.智子封锁
智子封锁
题目

题目分析
1.由于ab 容易数值过大,我们可以提前计算10的c次方,方便提前取模
2.查看b是否是奇数,如果是奇数则让a*a一次然后进行取模,如果是偶数,则直接进行自乘,节省计算时间
代码
#include
#include // 用于pow函数,但这里我们手动实现幂运算以避免浮点误差 using namespace std; // 快速幂取模函数,用于计算(base^exp) % mod
long long fastPowMod( long long base , long long exp, long long mod)
{ long long result = 1; while (exp > 0){ if (exp % 2 == 1) { // 如果当前exp是奇数,则乘上当前的base result = (result * base ) % mod; } base = ( base * base ) % mod; // base自乘,准备下一次迭代 exp /= 2; // exp减半 } return result;
} int main(){ int a, b, c; cin >> a >> b >> c; // 计算10的c次方,用于取模 long long mod = pow(10, c); // 使用快速幂取模函数计算a的b次方对mod取模的结果 long long result = fastPowMod(a, b, mod); cout << result << endl; return 0;
}
5.加与计数
加与计数
题目

题目分析
1.观察题目例子,我们可以发现一件事,符合条件的(x,y)组合是对称的,即,只要我们确定了(x,y)符合要求,则(y,x)也肯定符合
2.右移x,y,按位与
代码
#include
#include
using namespace std;int tenintwo( int n, int m)
{while (n > 0 || m > 0) {// 检查最低位 int bitN = n & 1; // 提取n的最低位 int bitM = m & 1; // 提取m的最低位 // 如果n和m的最低位同时为1,则返回1 if (bitN && bitM) {return 1;}// 右移n和m,准备检查下一位 n >>= 1;m >>= 1;}// 所有位都检查过了,没有发现同时为1的位,返回0 return 0;
}int countPairs( int n)
{int count = 0;for ( int x = 1; x < n/2; ++x){int y = n - x;if (tenintwo(x, y) == 0){++count;}}return count*2;
}int main()
{int n;cin >> n;cout << countPairs(n) << endl;return 0;
}