给定长度为 \(n\) 的数列 \(p\),求有多少个长度为 \(n\) 的数列 \(a\) 满足:\(\forall i\in[1,n],|a_i|=1\);其前缀和数组排序后恰为数列 \(p\)。\(\sum n\leq 5000\)。
这个题真的抽象,还是先不管了。
Conclusion
-
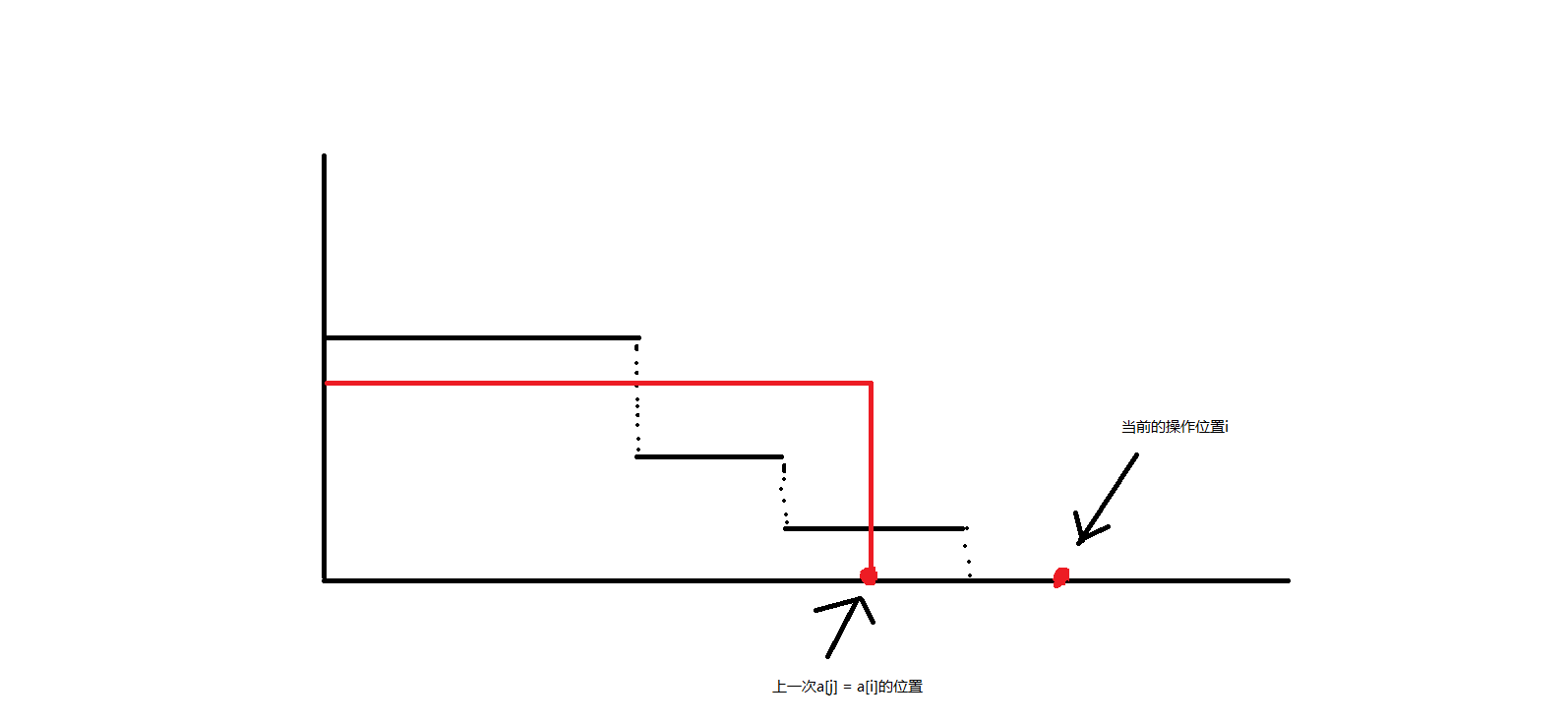
用折线图观察操作。
-
自定义统一操作生成最终答案。
-
题外话:感觉连续段 dp 也可做?https://www.luogu.com.cn/article/i8kmk5tr
给你一个长为 \(n\) 的非负整数序列 \(a\),求有多少区间 \([l,r]\) 满足 \(\text{popcount}(\max\limits_{i=l}^r a_i)=\text{popcount}(\min\limits_{i=l}^r a_i)\)。\(1\le n\le 10^6,0\le a_i\le 10^{18}\)。
Conclusion
- Min/Max 分治模型:

所以这个题我们 \(i\) 从 \(mid\) 到 \(l\) 走,动态指针维护 \(p,q\),然后分别计算这三段的贡献。(对于每个 \(l\) 计算合法的 \(r\))
具体来说每次枚举的就是 \(l'\),然后看 \(r'\) 在 \((mid,p],(p,q],(q,r]\) 分别有多少个即可。最麻烦的是第 2 种计算,这个时候我们讨论是哪一个在左边。
void dfs(int l, int r) {if(l == r) return ans ++, void();int mid = l + r >> 1;dfs(l, mid);dfs(mid + 1, r);pre[mid] = 0; mx[mid] = -1e18, mn[mid] = 1e18;for(int i = mid + 1;i <= r; ++i) mx[i] = max(mx[i-1], a[i]), mn[i] = min(mn[i-1], a[i]), pre[i] = pre[i - 1] + (pc(mx[i]) == pc(mn[i]));// 我们的桶维护 (p1, p2] 的 pop 个数 for(int i = mid, maxn = -1, minn = 1e18, p1 = mid, p2 = mid;i >= l; --i) {maxn = max(maxn, a[i]), minn = min(minn, a[i]);// p1while(p1 < r and maxn >= mx[p1 + 1] and minn <= mn[p1 + 1]) {++p1; --cnt1[pc(mx[p1])], --cnt2[pc(mn[p1])];}// p2while(p2 < r and (maxn >= mx[p2 + 1] or minn <= mn[p2 + 1])) {++p2; ++cnt1[pc(mx[p2])], ++cnt2[pc(mn[p2])];}// 1. <= p1if(pc(maxn) == pc(minn)) ans += p1 - mid;// 2. p1 < x <= p2,也就是一边 max 一边 min,比较有难度,分讨 maxmin 在哪边 if(maxn >= mx[p2]) // max 在左边 ans += cnt2[pc(maxn)]; // minelse // min 在左边ans += cnt1[pc(minn)];// 3. > p2,max/min 都在右边,左边完全不影响 ans += pre[r] - pre[p2]; // 那么就看 max 和 min pc 相等的 r' 个数即可 }memset(cnt1, 0, sizeof cnt1); memset(cnt2, 0, sizeof cnt2);
}