题目描述
年轻的自然主义者比尔在学校里研究蚂蚁。他的蚂蚁以生活在苹果树上的蚜虫为食。每个蚂蚁群需要自己的苹果树来养活自己。比尔有一张地图,上面标有 \(n\) 个蚂蚁群和 \(n\) 棵苹果树的坐标。他知道蚂蚁从它们的蚂蚁群到它们的取食地点,然后返回蚂蚁群,都是使用化学标记的路线。这些路线不能相交,否则蚂蚁会迷失方向,到达错误的蚂蚁群或树,从而引发蚂蚁群之间的战争。比尔希望将每个蚂蚁群连接到单独的苹果树,使得所有的 \(n\) 条路线都是不相交的直线。在这个问题中,这样的连接总是可能的。你的任务是编写一个程序来找到这样的连接。
\(n\leq 300\),坐标范围 \([0, 5000]\),任意三点不共线。
solution
二分图匹配十分困难。有一个极端 \(O(n^4)\) 以上的暴力,直接在平面上建网络流的图,将 \(O(n^4)\) 个交点全部建出来,然后将要连接的一对点用一条链把它们和线上的所有交点全部连起来,并要求交点的流量不超过 \(1\),跑普通的二分图匹配。
考虑一个事情:平面上如果 \(AB\) 与 \(CD\) 有交,我们需要将其调整为 \(AC\) 和 \(BD\)(或 \(AD\) 与 \(BC\))。
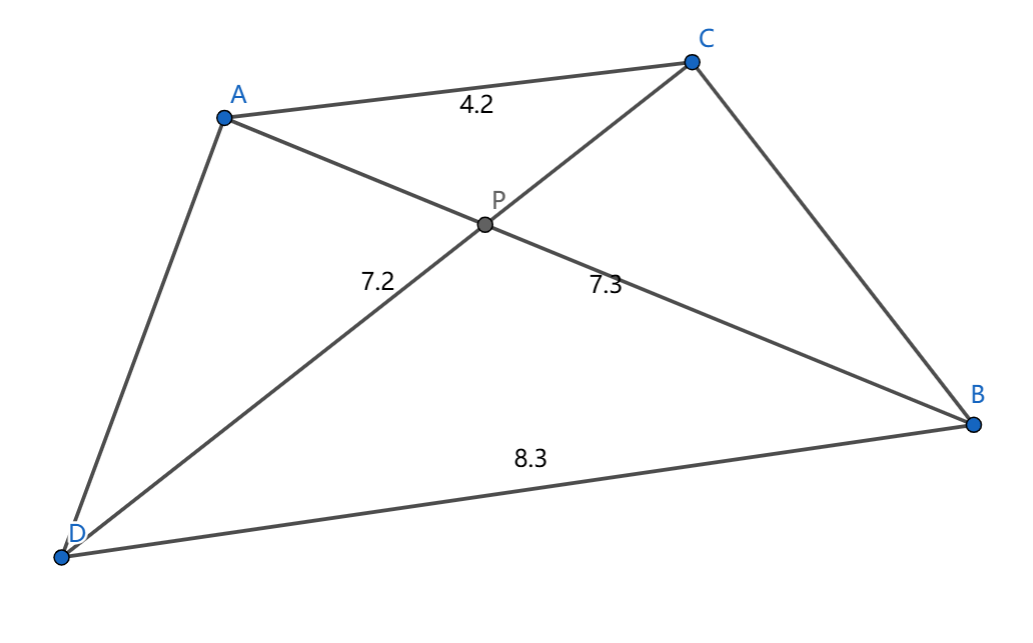
我们有四边形不等式:\(AC+BD<AB+CD\)。意思就是,如果现在存在一组匹配,我们可以将其调整使得长度和更小的话,我们直接调整之,必然更加合法。
连出 \(O(n^2)\) 条边,使用你喜欢的算法跑二分图最大权匹配即可。
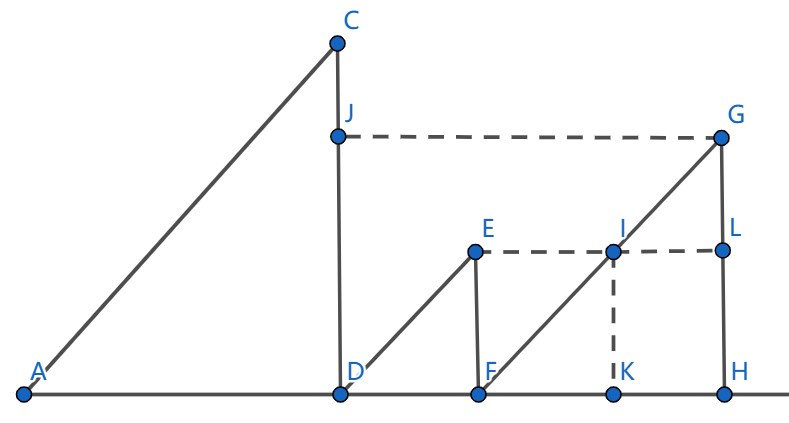
四边形不等式证明
因为 \(AP+CP>AC\) 且 \(DP+BP>BD\),所以 \(AB+CD>AC+BD\)。
code
【模板】网络流的求法 - caijianhong - 博客园 (cnblogs.com) 这里抽取最后一个板子,然后:
int n;
complex<double> a[310], b[310];
int main() {
#ifndef LOCALcin.tie(nullptr)->sync_with_stdio(false);
#endifcin >> n;for (int i = 1; i <= n; i++) {int x, y;cin >> x >> y;a[i].real(x), a[i].imag(y);}for (int i = 1; i <= n; i++) {int x, y;cin >> x >> y;b[i].real(x), b[i].imag(y);}mcmf_graph<int, double> mf(n * 2 + 2);for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) mf.add(i, n + j, 1, abs(a[i] - b[j]));}for (int i = 1; i <= n; i++) mf.add(0, i, 1, 0);for (int i = 1; i <= n; i++) mf.add(i + n, n * 2 + 1, 1, 0);mf.flow(0, n * 2 + 1);int cnt = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (!mf.g[cnt].w.first) cout << j << " \n"[i == n];cnt += 2;}}return 0;
}