AT_arc184_d [ARC184D] Erase Balls 2D
首先,假定我们选定的行为 \(i_1,i_2,\cdots,i_k\),并有 \(i_1<i_2<\cdots<i_k\),则 \(p_{i_1}>p_{i_2}>\cdots>p_{i_k}\)。其中 \(p_x\) 表示 \((x,p_x)\) 的位置上有点。
最终状态形如下图。显然,这种状态与操作顺序无关。
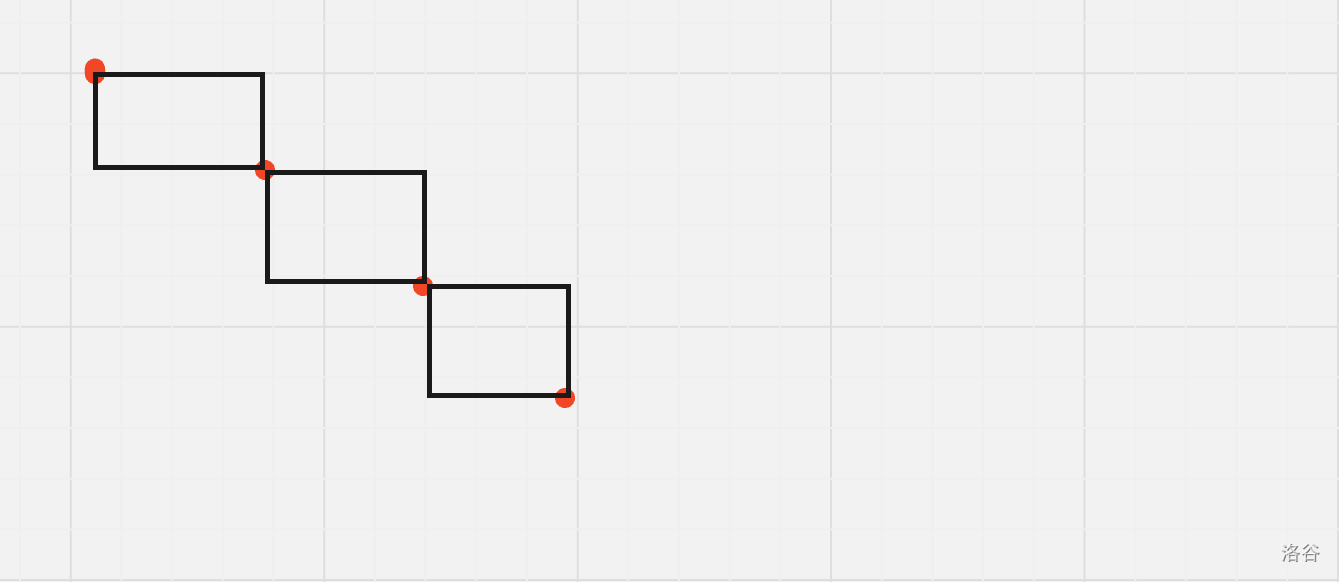
为了方便统计,加入 \((0,n+1)\) 与 \((n+1,0)\),并钦定这两个点必须选上。
加入枚举选的点集 \(S=\{(i_1,p_{i_1}),(i_2,p_{i_2})\cdots,(i_k,p_{i_k})\}\),令最终保留的点集为 \(T\)。直接统计 \(S\) 的方案会算重,考虑对于每个点集 \(T\) 设定一个唯一的点集 \(S\) 与之对应。
对于每个 \(T\),一般的想法是选择 \(|S|\) 极值下的情况,考虑这两种方法是否成功:
-
选取 \(|S|\) 最少,考虑一例子:\((1,2),(2,1),(3,3)\),选取 \(S=\{(1,2)\}\) 或是 \(\{(2,1)\}\) 所对应的保留的点集 \(T\) 是相同,所以统计起来还需要额外增加条件。
-
选取 \(|S|\) 最多,这个 \(S\) 显然是唯一的。具体的,可以考虑一个结束状态 \(T\),通过不断将 \((x,p_x)\) 加入 \(S\) 中的方法,得到唯一性。
这样的话就比较容易了,考虑令 \(f_{i}\) 表示考虑了前 \(i\) 个,\((i,p_i) \in S\) 的总方案数。每次枚举上一个点 \(j\),判断 \((j,p_j)\) 与 \((i,p_i)\) 所得到的矩形内的点是否满足:任意选择一个点,都会使得有一个矩形内的点被删除。
这个判断容易的,用前缀最小值与后缀最大值 \(O(n)\) 判断即可。
复杂度 \(O(n^3)\)。感觉 2804 的评分有点虚高……
#include <bits/stdc++.h>
using namespace std;#define vi vector<int>
#define pb push_back
#define pii pair<int,int>
#define mkp make_pairint rd() {int x = 0, f = 1;char ch = getchar();while (!('0' <= ch && ch <= '9')) {if (ch == '-') f = -1; ch = getchar();}while ('0' <= ch && ch <= '9') {x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar();}return x * f;
}void wr(int x) {if (x < 0) putchar('-'), x = -x;if (x >= 10) wr(x / 10); putchar(x % 10 + '0');
}const int N = 310;
const int mod = 998244353;int f[N];
int n, x[N], y[N], pos[N];
int cnt, b[N], preb[N], sufb[N];bool check() {for (int i = 1; i <= cnt; ++i)preb[i] = sufb[i] = b[i];for (int i = 2; i <= cnt; ++i)preb[i] = min(preb[i - 1], preb[i]);for (int i = cnt - 1; i >= 1; --i)sufb[i] = max(sufb[i + 1], sufb[i]);for (int i = 2; i <= cnt - 1; ++i) {if (preb[i] >= b[i] && b[i] >= sufb[i]) return false; }return true;
}int main() {ios::sync_with_stdio(false); cin.tie(0);cin >> n;for (int i = 1; i <= n; ++i) {int x, y; cin >> x >> y; pos[x] = y; }f[0] = 1; pos[0] = n + 1;for (int i = 1; i <= n + 1; ++i) {for (int j = 0; j < i; ++j) {if (pos[i] > pos[j]) continue; cnt = 0; for (int k = j; k <= i; ++k) {if (pos[i] <= pos[k] && pos[k] <= pos[j])b[++cnt] = pos[k]; }if (check()) f[i] = (f[i] + f[j]) % mod; }}cout << f[n + 1] << endl; return 0;
}