pub fn f1(mut n: u32) -> u32 {n = n | (n >> 1);n = n | (n >> 2);n = n | (n >> 4);n = n | (n >> 8);n = n | (n >> 16);n
} 如果n的输入类型为 u32(32位无符号整型), 上述代码的结果为大于等于n的2^k - 1的值(因为可能会出现溢出,所以并没有直接返回2^k),二进制表现为从最高有效位开始全为 1,例:n = 00001010, 则返回值的二进制为 00001111。如果是 u64,只需在函数里再加上 n = n | (n >> 32)。以下是我对于上述代码的理解。
我们思考代码如何运行的时候,只需要记住,原n的二进制的最高有效位是关键,其它位置不重要。假如 n = 17, n 的 u8 二进制为 00010001,运行上述代码会返回 31,二进制为 00011111。
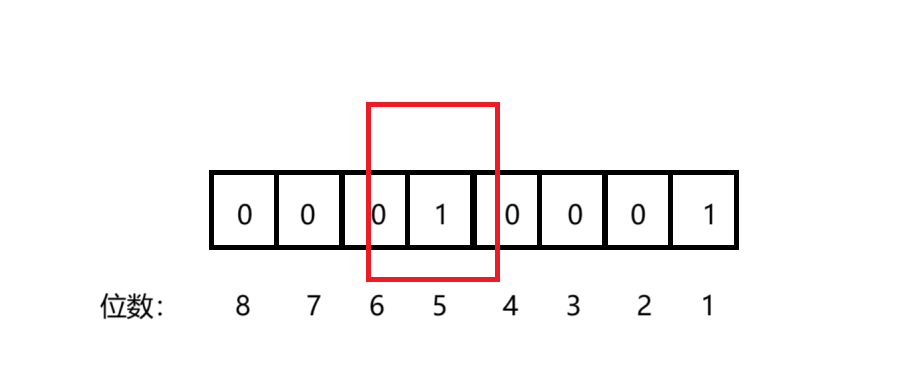
在执行n = n | (n >> 1) 时,目的是让前 2 位最高有效位变为 1,
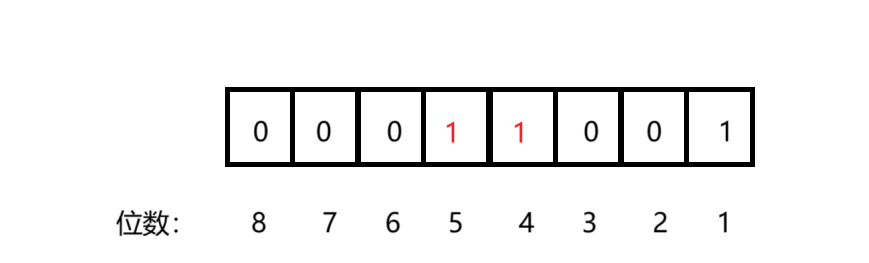
在执行n = n | (n >> 2) 时,目的是让前 4 位最高有效位变为 1,
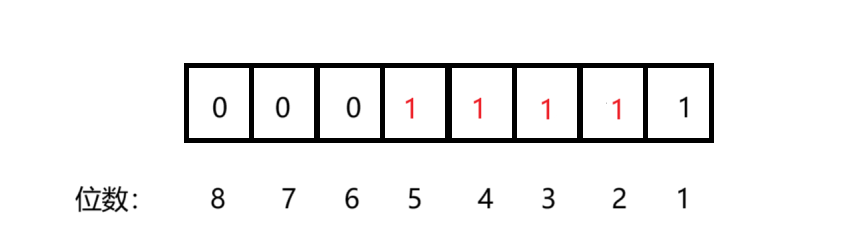
根据以上规律,代码执行到返回的结果就是从最高有效位开始,所有位数的值都为1,结束!