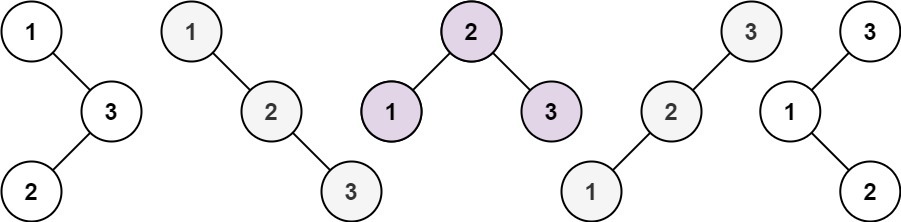
n(24)位的排列,有m个形如 \((a_i,b_i,c_i)\) 的限制,要求排列中 \(b_i\) 需要出现在 \(a_i\) 和 \(c_i\) 之间,求满足条件排列个数。
由 n 的范围想到状压 dp。dp 排列的方式有很多种,如果是多项式级别的话可能是按顺序填数枚举当前填的数在已经填入的数中的 rank。这道题是状压,有两种可能:状压已经填入的格子按顺序填数,或状压已经填入的数按顺序填入格子。由于限制是在具体的数和相对位置上的,用后者比较合适。
直接 dp,暴力判断当前状态可不可以加入一个数 x。对于一个限制 (a,b,c),它对于状态的限制可以只在加入 b 时考虑,即无条件加入 a 和 c,只在加入 b 的时候看违不违背 (a,b,c)。具体来说,往当前集合 S 加入 b 时,如果 a c 同时 (在/不在) S 中,则不合法,容易证明这等价于每加入一个 a/b/c 就考虑限制 (a,b,c)。这样是 \(O(n^32^n)\) 的。(比较难卡,实现的好可以暴打标算)
法一:正攻,考虑对每一个 b 预处理出哪些 S 加入 b 时合法。即 S 中只存在 a 不存在 c 或 只存在 c 不存在 a。我们把中间为 b 的所有限制 \((a_i,b,c_i)\) 拿出来,可以看到会有若干个 \(a_i\) 和 \(c_i\) 在 \(b\) 的两边的要求。考虑到两个限制之间存在相同的 a/c 会相关联,将 \(a_i\) 与 \(c_i\) 连边建图,一个连通图里应该满足是个二分图,且两个连通图间互不影响。二分图内同属一边的点也同在 b 的一边,所以我们可以得到若干个集合对 \((U_i,V_i)\),表示集合 \(U_i\) 必须同在 b 的一边并且 \(V_i\) 同在另一边,不同的集合对相互独立。回头考虑合法的 S,这个 S 可以看作是 b 的左边的所有点,所以它应该可以由每对 \((U_i,V_i)\) 选一个集合全部并起来得到。对于每个 b,获取 \((U_i,V_i)\) 并枚举所能生成的所有的 S,这是 \(O(n2^n)\) 的。实际上,忽略那些与 b 无关的数,每个二分图至少有两个点,最多只有 \(\frac{n}{2}\) 个集合对,可以优化到 \(O(n2^{\frac{n}{2}})\)。最终的复杂度还是取决于 dp 复杂度,是 \(O(n2^n)\)。
法二:正难则反,考虑对每一个 b 预处理出哪些 S 加入 b 时不合法。这样之所以会更简单是因为一旦 S 中的一个子结构违背了某个 (a,b,c),那么不管其他位的状态如何,S 始终是不合法的。与合法时必须要求对所有 (a,b,c) 合法不同,不合法只需要对某个 (a,b,c) 不合法即可,不需要考虑包含 b 的所有 \((a_i,b,c_i)\) 的整体结构。具体来说,对每个 (a,b,c) 所有 a c 对应位同为 0 与同为 1 的 S 都应被标记为不合法。这很容易用高维前缀和解决。如果对每个 b 做前缀和是 \(O(n^22^n)\),但我们可以把前缀和的数组设置为状态 S 对哪些 b 不合法,这样只需要一次前缀和 \(O(n2^n)\)。这个算法不如法一快是因为高维前缀和与 dp 都是 \(O(n2^n)\) 的,相当于一个两倍常数。
法三:重新考虑集合合法性的问题。我们之前提到对于 (a,b,c),同时存在 a c 则无法加入 b。但事实上,同时存在 a c 本就是不合法状态,可以在加入 b 之前就判断其不合法。于是我们可以转变思路,考虑 S 状态本身是否合法。延续法二的思路,还是考虑不合法的 S,由于这次我们没有钦定 b,某个 (a,b,c) 会对 S 里对应的三位有限制。S 对于 (a,b,c) 不合法等价于 \(S_a=S_c=1,S_b=0\) 或 \(S_a=S_c=0,S_b=1\),这个可以用带容斥的高维前缀和解决,复杂度 \(O(n2^n)\)。类似的,这个做法也跑的比法一慢。
注:法二和法三遇到的是同一类问题,即给定集合 \(A=\{a_0,a_1,\cdots,a_p\}\) 和 \(B=\{b_0,b_1,\cdots,b_q\}\),钦定二进制表示的集合 S 中的 \(S_{a_i} = 0\) 且 \(S_{b_i}=1\),其他位可以为 0 也可为 1,并对于所有满足条件的 S,做操作 \(f_S+=c\)。如果 B 是空集,就可以转化为对所有 \(S\sube U\backslash A\) 做上述操作,如果 A 是空集,可以转化为对所有 \(S\supe B\) 做上述操作。如果两个集合都有元素,则可以先假设其中一个为空集,然后容斥掉多操作的部分。不过值得注意的是,法二中的操作不是加等于而是或等于,这导致无法容斥,但具体需求正好满足可以分为两部分来做,其中每一个部分都是有一个集合是空集的问题,刚好不需要容斥。


![SQLSTATE[42S22]: Column not found: 1054 Unknown column Color in field list](https://img2024.cnblogs.com/blog/1295962/202407/1295962-20240717124854088-281169181.jpg)
![P9752 [CSP-S 2023] 密码锁P8814 [CSP-J 2022] 解密](https://img2024.cnblogs.com/blog/3503983/202410/3503983-20241003214918313-370669270.png)