20241003

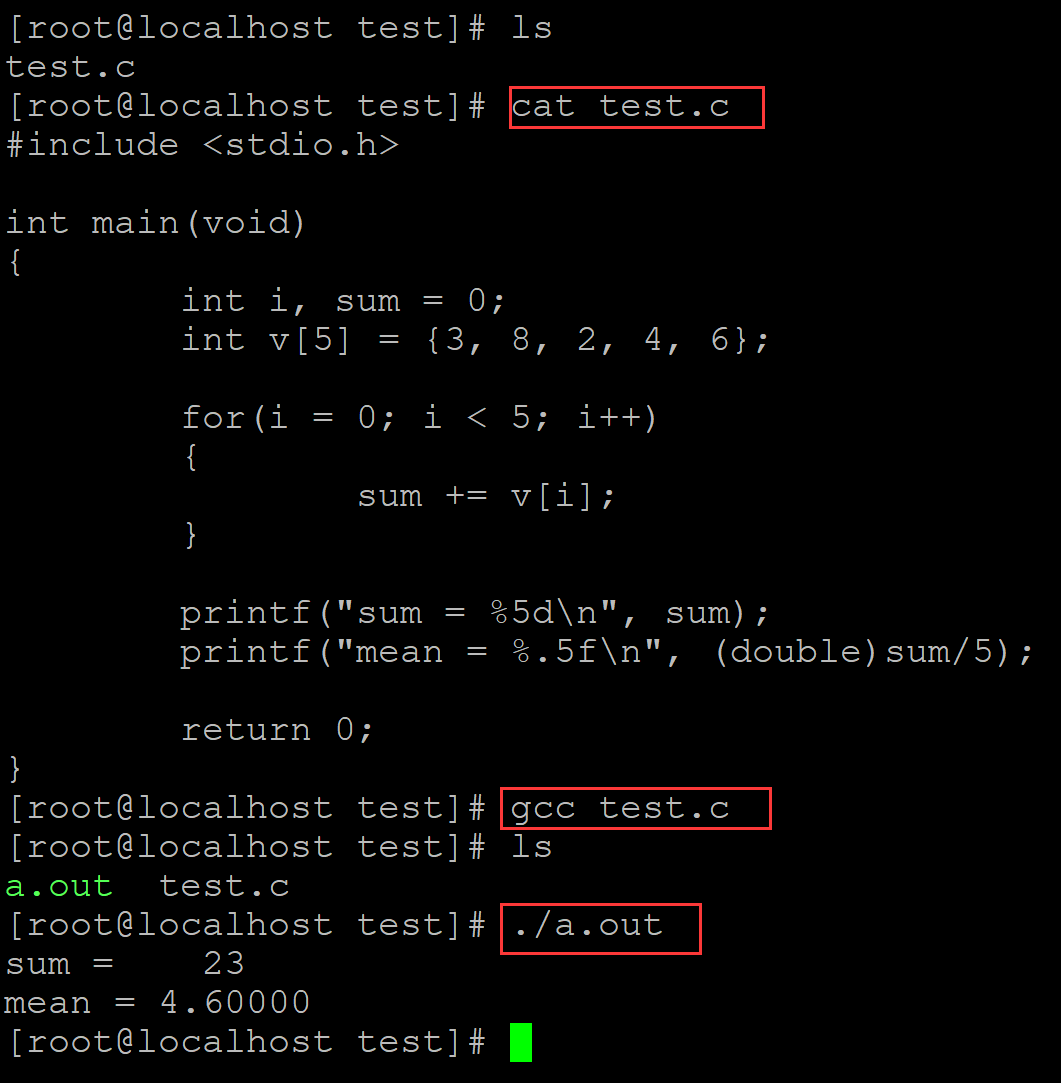
公交车(bus)

显然的题目,答案就是所有连通块的大小减一之和

#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 1e7 + 5;int n, m, fa[N], sz[N], ans;int find(int x) {if (fa[x] == x) {return x;}return fa[x] = find(fa[x]);
}void merge(int x, int y) {x = find(x), y = find(y);if (x != y) {fa[x] = y;sz[y] += sz[x];}
}signed main() {ios::sync_with_stdio(0);freopen("bus.in", "r", stdin);freopen("bus.out", "w", stdout);cin >> n >> m;for (int i = 1; i <= n; i++) {fa[i] = i;sz[i] = 1;}for (int i = 1, u, v; i <= m; i++) {cin >> u >> v;merge(u, v);}for (int i = 1; i <= n; i++) {ans += max(0ll, (find(i) == i) * (sz[i] - 1));}cout << ans;return 0;
}

出租车(taxi)

我们可以设 \(dp_{i, j}\) 表示从后往前选到第 \(i\) 个数,左端点与右端点的差值 (左右端点就是 \(a, b\) 两个排列分别选到了哪里),最优化属性为最少用了几次单体技(也就是单独移动一次左或右端点),那么如果 \(a_i !\neq b_{i, j}\)(用 \(i - j\) 就可以得到 \(b\) 数组中的对应下标)显然 \(dp_{i, j} = dp_{i + 1, j}\),那么如果 \(a_i = b_{i - j}\), 就是\(dp_{i, j} = min(dp_{i + 1, j - 1}, dp_{i + 1, j + 1}) + 1\) ,显然可以先用滚动数组优化掉第一维,但是第二种转移才是真正有影响的,而第二种转移每次只会有一次,所以我们的时间复杂度就是 \(O(n)\)

#include <bits/stdc++.h>using namespace std;const int N = 1e6 + 5;int n, a[N], b[N], dp[N], pos[N], p[N];int main() {ios::sync_with_stdio(0);cin.tie(0);freopen("taxi.in", "r", stdin);freopen("taxi.out", "w", stdout);cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}for (int i = 1; i <= n; i++) {cin >> b[i];pos[b[i]] = i;}for (int i = 1; i <= n; i++) {p[i] = n + i - pos[a[i]];}for (int i = 0; i < n; i++) {dp[i] = 1000000;}for (int i = n; i <= 2 * n; i++) {dp[i] = i - n;}for (int i = n; i >= 1; i--) {dp[p[i]] = min(dp[p[i] + 1], dp[p[i] - 1]) + 1;}cout << n + dp[n] / 2;return 0;
}

出租车(taxi)

我们先最简单的考虑一个小正方形的染色,一个小正方形总共有 \(4\) 个角,染三种颜色,必然会有两个角的颜色相同,如下图:

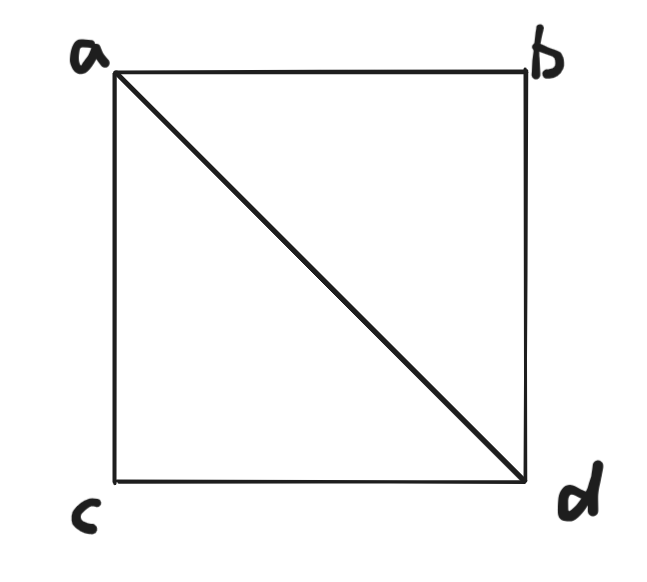
那么 \(a\) 与 \(d\) 的颜色必然不能相同,那么 \(c \neq a 且 c \neq d\) , \(b \neq a 且 b \neq d\),那么 \(c\) 必然等于 \(d\) ,也就是说其实我们知道了这个正方形中的任意两个点就可以推出剩下的两个点.

如图:

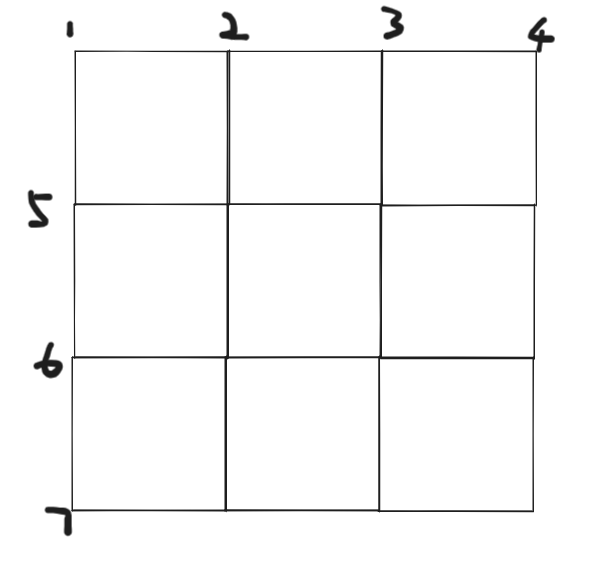
我们其实只用知道 \(1, 2, 3, 4, 5, 6, 7\) 的颜色即可,那么这就是一个 \(O(2 ^ {n + m})\) 的做法,为啥不是 \(3 ^ {n + m}\)的时间复杂度,因为我们还要保证当前的颜色与前面的不同,所以只有两种选择了,

看下图:

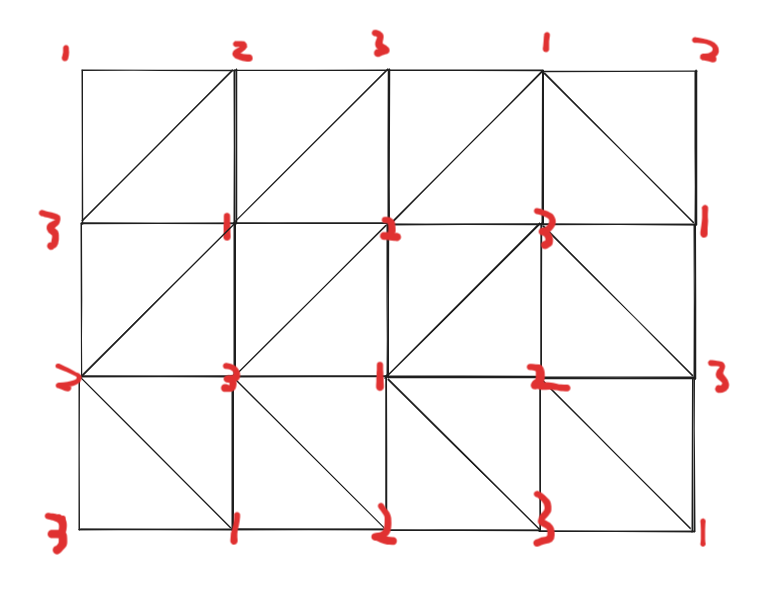
接下来找规律即可

#include <bits/stdc++.h>using namespace std;#define int long longconst int N = 5e2 + 5;int t, n, m, fa[N * 4];char ans[N][N], c[N][N];int find(int x) {if (fa[x] == x) {return x;}return fa[x] = find(fa[x]);
}void merge(int x, int y) {x = find(x), y = find(y);if (x != y) {fa[x] = y;}
}void Solve() {cin >> n >> m;for (int i = 1; i <= 2 * (n + m); i++) {fa[i] = i;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> c[i][j];if (c[i][j] == 'N') {merge(j, m + i);merge(j + (n + m), m + i + (n + m));ans[i][j] = 'N';}else if (c[i][j] == 'Z') {merge(j, m + i + (n + m));merge(j + (n + m), m + i);ans[i][j] = 'Z';}}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {if (c[i][j] != '?') {continue;}if (find(m + i) != find(j + (n + m)) && find(j) != find(m + i + (n + m))) {merge(j, m + i);merge(j + (n + m), m + i + (n + m));ans[i][j] = 'N';}else {merge(j, m + i + (n + m));merge(j + (n + m), m + i);ans[i][j] = 'Z';}}}for (int i = 1; i <= n + m; i++) {if (find(i) == find(i + n + m)) {cout << "0\n";return ;}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << ans[i][j];}cout << "\n";}
}signed main() {ios::sync_with_stdio(0);cin.tie(0);freopen("bike.in", "r", stdin);freopen("bike.out", "w", stdout);cin >> t;while (t--) {Solve();}return 0;
}