换根 dp 模板题。
\(f_i\) 是在以 \(i\) 为根的子树中,以 \(i\) 为链的一个端点且 \(i\) 在点集中的合法点集个数。
\(ans_i\) 表示包含 \(i\) 的合法点集个数。
当 \(x\) 为树根时:
\[ans_x = {f_x \choose 2} - \sum_{s\in son}{2f_s+1 \choose 2} + f_x
\]
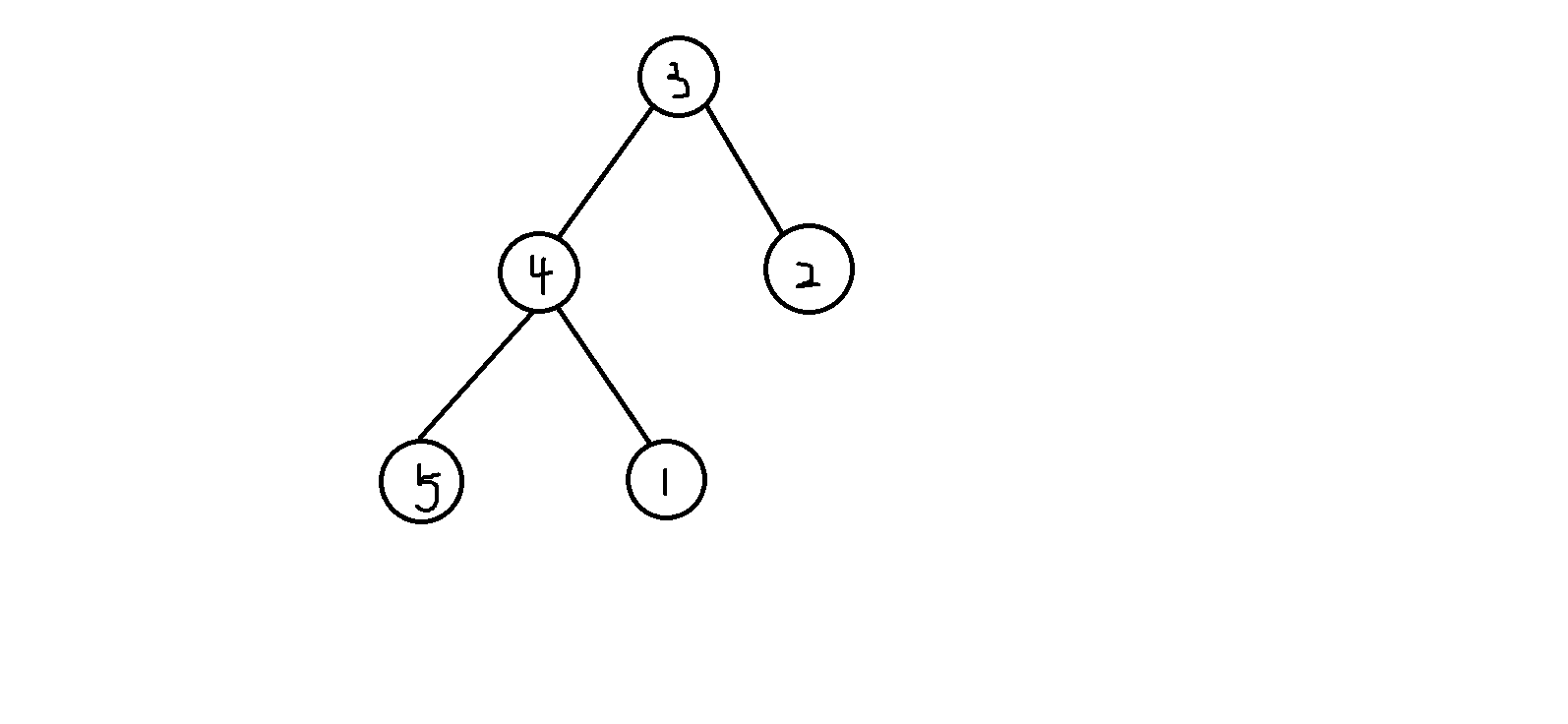
简单解释一下,\({f_x \choose 2}\) 是在所有符合条件的链中随便选两条拼起来的数量,但是有可能会选到同一个子树中的两条链,这样拼起来的集合就不合法了,就像样例解释中的 \(\{1,3,4\}\) 一样,所以要减去。最后加上以 \(x\) 为链的一端的数量,也就是不需要拼的。
\(f_i\) 很好维护:
\[f_x= \sum_{s \in son}2f_s+1
\]
\(f_s\) 要乘 \(2\) 是因为 \(s\) 这个点可以选可以不选。即有可能是 \(\{\dots, s, x\}\),也有可能是 \(\{\dots, x\}\)。
加一是因为要加上集合为 \(\{s, x\}\) 的情况。
换根的时候根据上面的公式改下 \(f\) 数组就可以了。\(\sum{2f_s+1 \choose 2}\) 的部分用数组预处理出来就好了。
具体实现看代码。
#include <bits/stdc++.h>using namespace std;#define int long longint read() {int s = 0, w = 1;char c = getchar();while (!isdigit(c)) {if (c == '-')w = -w;c = getchar();}while (isdigit(c)) {s = s * 10 + c - 48;c = getchar();}return s * w;
}
void pr(int x) {if (x < 0)putchar('-'), x = -x;if (x > 9)pr(x / 10);putchar(x % 10 + 48);
}
#define end_ putchar('\n')
#define spc_ putchar(' ')const int maxN = 5e5 + 7, mod = 1e9 + 7;const int m2 = 500000004;
// 2 的逆元int n;vector<int> E[maxN];int f[maxN], s[maxN], A[maxN], ans;
// s 数组是预处理公式中求和的部分, A[i] 为 ans[i]int C(int x) {return x * (x - 1 + mod) % mod * m2 % mod;
}void dfs(int x, int fa) {for (int to : E[x])if (to != fa) {dfs(to, x);f[x] += f[to] * 2 + 1;f[x] %= mod;s[x] += C(f[to] * 2 + 1);s[x] %= mod;}
}int ff[maxN];void calc(int x, int fa) {A[x] = ((C(f[x]) - s[x] + mod) % mod + f[x]) % mod;for (int to : E[x]) {if (to == fa)continue;int fx = f[x], fto = f[to];int S = s[to];f[x] -= f[to] * 2 + 1;f[x] = (f[x] + mod * 2) % mod;// 这里要注意乘 2,因为上面的 f[to] 乘 2 了,只加一个 mod 有可能不够。f[to] += f[x] * 2 + 1;f[to] %= mod;s[to] += C(f[x] * 2 + 1);s[to] %= mod;calc(to, x);f[x] = fx, f[to] = fto;s[to] = S;}
}signed main() {n = read();for (int i = 1; i < n; i++) {int u = read(), v = read();E[u].emplace_back(v);E[v].emplace_back(u);}dfs(1, 0);calc(1, 0);for (int i = 1; i <= n; i++)ans ^= A[i] * i;pr(ans), end_;
}