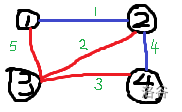
分层图
前言
在一次模拟赛中,我遇到了 [USACO15JAN] Grass Cownoisseur G 这道题,当时不知如何下手,和边上的同学偷偷讨论,听别人说是分层图,建两份图然后连一层反向边即可,当时对这个图论建模大为惊叹(不亚于我在学网络流时学到拆点拆边),故专门写一篇博客记录之。
算法思想
分层图是图论建模的一个巧妙的工具,主要用来解决类似以下形式的问题:
在图中求最短路,但可以做不多于 \(k\) 次的特殊转移,求最短路。
一般题目中的 \(k\) 不会较大
对于这种题目,可以使用分层图解决。
方法是建立 \(k + 1\) 层架构与原图相同的图,然后将特殊转移用有向边的形式连接第 \(i\) 层和第 \(i + 1\) 层节点,则可以使用图论建模来描述原图的 \(k\) 次决策。
例题
[USACO15JAN] Grass Cownoisseur G
题意:给定一个 \(n\) 点 \(m\) 边的有向图,节点编号 \(1 \dots n\)。
定义一条路径的长度为该路径上经过的所有不同的节点的总数,求 \(1\) 到 \(1\) 的最长路。
特殊转移:可以在任意时刻走最多一次反向边。
这道题是我在考场上遇到的题目,当时并未场切,丢人丢大了。
首先,建两份与原图相同的图,对于原图节点 \(i\),其在第二层图的对应节点为 \(i + n\),用反向边连接两层图。
for (int i = 0; i < m; i++)
{read(u), read(v);add_edge(v, u + n); // 跨层级反向边add_edge(u, v), add_edge(u + n, v + n); // 建两份图
}
考虑到原题要求最长路,而原图全都是正权环,因此要先 \(\text{Tarjan}\) 缩点再求最短路。
同时,注意到 \(\text{Tarjan}\) 缩点具有性质:\(\text{SCC}\) 编号恰为逆拓扑序,则可以考虑直接逆拓扑序 \(\text{DP}\),显然有转移:
其中 \(E\) 为边集,\(d_u\) 为缩点 \(u\) 到缩点 \(1\) 的距离,\(w_u\) 为缩点 \(u\) 包含的节点数量。
for (int u = id[1]; u; u--)for (auto &&v : DAG[u])chkmax(dis[v], dis[u] + cnt[v]);
则答案为 \(d_{1 + n}\)。
有的题解会说答案为 \(\max{d_1, d_{1 + n}}\),其实不然。
以 \(\text{DP}\) 的形式计算贡献默认了 \(d_1\) 为 \(0\),统计 \(d_1\) 无意义。
而且经过反向边的最长路一定不会比不经过反向边要劣,因为可以经过反向边后立即经过正向边。
因此直接统计 \(d_{1 + n}\) 即可。
总代码:
#include <bits/extc++.h>#define inline __always_inline
template <typename T> inline void chkmin(T &x, const T &y) { if (x > y) x = y; }
template <typename T> inline void chkmax(T &x, const T &y) { if (x < y) x = y; }
template <typename T> inline void read(T &x)
{char ch;for (ch = getchar(); !isdigit(ch); ch = getchar());for (x = 0; isdigit(ch); ch = getchar()) x = x * 10 + ch - '0';
}
const int MaxN = 2e5 + 5;int n, m, u, v;
std::vector<int> graph[MaxN], DAG[MaxN];
inline void add_edge(int u, int v) { graph[u].push_back(v); }
char visit[MaxN];
int dis[MaxN], cnt[MaxN], id[MaxN], low[MaxN], dfn[MaxN], cur = 1, scc = 1;
int queue[MaxN], *head = queue, *tail = queue;
void tarjan(int u)
{low[u] = dfn[u] = cur++;visit[*tail++ = u] = 1;for (auto &&v : graph[u])if (!visit[v])tarjan(v), chkmin(low[u], low[v]);else if (visit[v] == 1)chkmin(low[u], dfn[v]);if (low[u] == dfn[u]){while (*tail != u)cnt[id[*--tail] = scc]++, visit[*tail] = 2;scc++;}
}int main()
{read(n), read(m);for (int i = 0; i < m; i++)read(u), read(v), add_edge(v, u + n), add_edge(u, v), add_edge(u + n, v + n);n <<= 1;for (int u = 1; u <= n; u++)if (!dfn[u]) tarjan(u);for (int u = 1; u <= n; u++)for (auto &&v : graph[u])if (id[u] != id[v])DAG[id[u]].push_back(id[v]);for (int u = id[1]; u; u--)for (auto &&v : DAG[u])chkmax(dis[v], dis[u] + cnt[v]);printf("%d", dis[id[1 + (n >> 1)]]);return 0;
}