【软考】3 校验码

news/2025/5/16 3:02:49/文章来源:https://www.cnblogs.com/mindzone/p/18447148

校验码

码距概念：任意进制的两个码值之间的最小二进制位数称为校验码的码距

例如：二进制1bit位，从0到1，则码距是1，二进制2bit位从 00 到 11 一共4个码字，但码距还是为1

可以设置性别男为 00 女为 11两个合法码字，则该两个合法码字的最小码距为2 （间隔 01 和 10 两个）

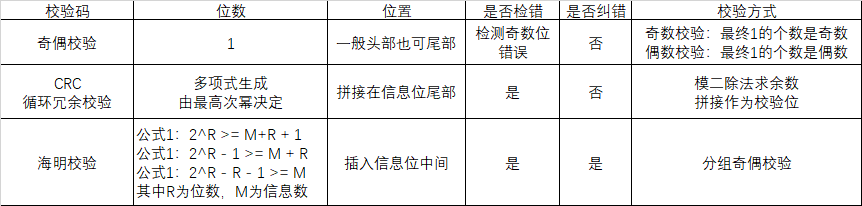
考点1: 奇偶校验码

奇偶校验码的编码方法是:由若干位有效信息(如一个字节) ,再加上一个二进制位(校验位)组成校验码。
奇校验:整个校验码(有效信息位和校验位)中“1” 的个数为奇数。
偶校验:整个校验码(有效信息位和校验位)中“1” 的个数为偶数。

检查1位（奇数位）的错误，不可纠正错误

考点2: CRC循环冗余校验码

CRC的编码方法是:在 K 位信息码之后拼接 R 位校验码。只能检测错误，不可纠错
应用CRC码的关键是如何从k位信息位简便地得到r位校验位(编码) ,以及如何从 K + R 位信息码判断是否出错。

1、把接收到的CRC码用约定的生成多项式G(X)去除(模二除法)，
2、如果正确，则余数为0;如果某一位出错，则余数不为0。
3、不同的位数出错其余数不同，余数和出错位序号之间有唯一的对应关系。

考点3: 海明校验码

海明校验码的原理是:
在有效信息位中加入几个校验位形成海明码，使码距比较均匀地拉大，并把海明码的每个二进制位分配到几个奇偶校验组中。
当某一位出错后，就会引起有关的几个校验位的值发生变化，这不但可以发现错误，还能指出错误的位置，为自动纠错提供了依据

校验位求取公式：

推导公式1 2^R >= M + R + 1

推导公式2 2^R - 1 >= M + R

其中R为校验位值，M为信息位的个数

三种校验码的特性区分

例题：

例题一、以下关于海明码的叙述中，正确的是( )。
A、海明码利用奇偶性进行检错和纠错
B、海明码的码距为1
C、海明码可以检错但不能纠错
D、海明码中数据位的长度与校验位的长度必须相同

解题思路：

C选项，海明码可以检错也可以纠错，所以排除

D选项，数据位 M = 16时，校验位 R >= 5 所以不是必须相同，排除

B选项，校验码一定是通过扩大码距实现校验的，而海明码的码距必然大于1，排除

A选项，海明码使用分组奇偶校验实现，所以正确

例题二、海明码是一种纠错码，其方法是为需要校验的数据位增加若干校验位，使得校验位的值决定于某些被校位的数据，
当被校数据出错时, 可根据校验位的值的变化找到出错位，从而纠正错误。对于32位的数据，至少需要增加( ) _个校验位才能构成海明码。
以10位数据为例，其海明码表示【D₉D₈D₇D₆D₅D₄D₃D₂D₁P₃D₀P₂P₁】中，其中D_i (0 ≤ i ≤ 9) 表示数据位，P_j(1 ≤ j ≤ 4)表示校验位，
数据位D₉由P₄P₃和P₂进行校验(从右至左D₉的位序为14,即等于8+4+2,因此用第8位的P₄、第4位的P₃和第2位的P₂校验) ，数据位D₅由( )进行校验。