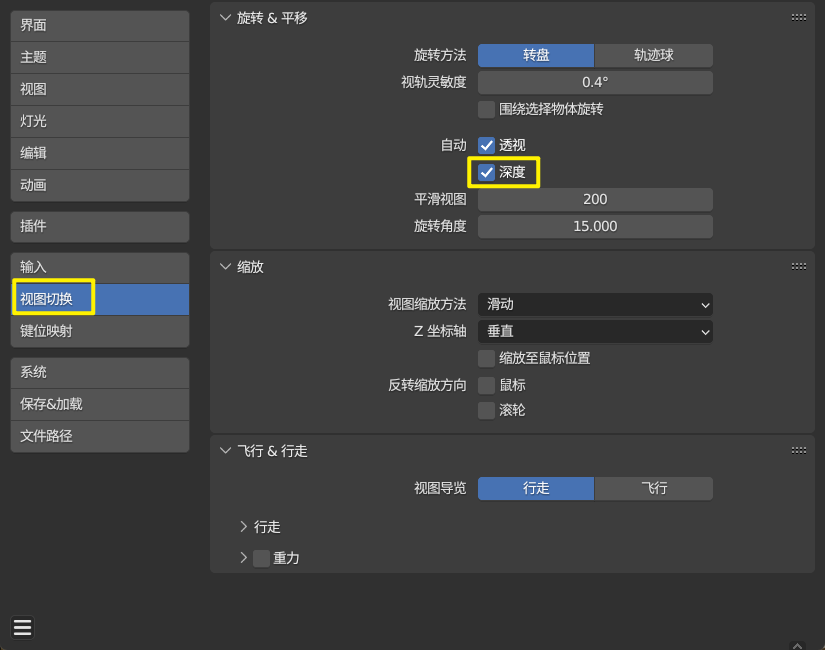
\(purfer\) 序列,是为了证明 \(cayley\) 定理。具体来说,是将一个树映射到一个数组上,在数组上可以使得很多东西更加清晰的展示。
构造 \(prufer\) 序列
\(prufer\) 是将一个大小为 \(n\) 的树映射到长度 \(n - 2\) 的序列上。从一个无根树开始,我们将树入度为 \(1\) 的点找出来,及叶子节点。 将编号最小的节点的链接的点加入 \(prufer\) 序列。再将这个点删除。重复操作直到只有两个节点。
\(prufer\) 序列还原树
\(prufer\) 序列中存在的树一定不是叶子节点,由于我们是先将最小的删除所以我们确定了当前不在 \(prufer\) 序列中的最小点的父亲。再将当前点去掉,重新求最小的不在 \(prufer\) 序列树,重复操作就可以了。
\(prufer\) 带来了什么
\(prufer\) 序列是最短的描述树的方式。首先,\(prufer\) 的最小先出的思想完善了每个树的父亲。最后可以留下两个点是因为根节点没有父亲,以及另一个非根节点的父亲确定,如果有 \(3\) 个节点很容易证明无法确定。
这样我们得到了最小的表示树的序列。同时,以为 \(prufer\) 描述了根节点和没节点的父亲,使得树也确定了下来。
\(prufer\) 不同,构造出来的树也不同,也就十分显然了。
\(cayley\) 定理
\(cayley\) 定理表达了一个完全图的生成树的个数有 \(n ^{n - 2}\) 个,我们很容易通过 \(prufer\) 序列的唯一性。把 \(cayley\) 定理抽象成长度为 \(n - 2\) 的序列,序列每个元素大小为正整数且小于等于 \(n\) 的序列有多少个。我们由小学学习的方式都可以得到有 \(n ^{n - 2}\) 个。这证明了cayley 定理。
\(prufer\)序列应用
笔者学习 \(prufer\) 的初衷是构造一个深度更深的树。
我们直接随机一个 \(prufer\) 序列进行试验。
可以神奇的发现:构造出来的序列还原回去的树高来到了 \(\sqrt{n}\) 的大小。比直接随机的树更加优秀。
但是,这还不是上线,因为 \(prufer\) 序列的一一对应,我们任意得到的序列都可以构造出一个树。深度和 \(prufer\) 序列的元素个数有关,所有我们甚至可以钦定 \(prufer\) 元素个数,再重构。