- 一. 引言
- 二. 塑性应变增量推导
- 三. 弹塑性刚度矩阵推导
- 四. 塑性模量理解
- 五. 小结
一. 引言
弹塑性理论定义材料在荷载作用下的变形是弹性变形和塑性变形之和,其中研究塑性变形需要解决三个方面的问题:
①产生塑性变形的起点;
②产生塑性变形的方向;
③产生塑性变形的大小。
在塑性理论中,描述以上三个问题的工具被称为是塑性理论的三大支柱:屈服条件、流动法则和硬化规律,它们分别被定义为:
①屈服条件是确定开始产生塑性变形的应力条件,屈服函数通常为应力状态和内变量的函数;
\[f=f\Big(\sigma_{ij},q_n\Big)
\]
②流动法则是确定塑性应变增量方向(势函数法向)的法则,对于关联流动准则Q=f;
\[d\varepsilon_{ij}^p=\langle\lambda\rangle\frac{\partial Q}{\partial\sigma_{ij}}
\]
③硬化规律是确定塑性应变増量大小( 𝑑𝜆 )的规律,确定硬化规律实质上是要确定硬化参量(等向强化,随动强化)。
或者可以这样说,屈服条件确定了塑性变形的起点,流动法则确定塑性变形的方向,硬化规律(确定硬化参量)确定了塑性变形的大小。
二. 塑性应变增量推导
step 1. 应变分解:
\[d\varepsilon_{ij}=d\varepsilon_{ij}^e+d\varepsilon_{ij}^p
\]
step 2. 总应力计算:
\[d\sigma_{ij}=C_{ijkl}d\varepsilon_{ij}^e=C_{ijkl}\left(d\varepsilon_{kl}-d\varepsilon_{kl}^p\right)
\]
step 3. 一致性条件(加载过程中任何时刻,应力点总位于屈服面上):
\[df=\frac{\partial f}{\partial\sigma_{ij}}d\sigma_{ij}+\frac{\partial f}{\partial q_n}dq_n=0
\]
其中
\[dq_n=\langle\lambda\rangle r_n
\]
\(q_n\)表示材料硬化状态, 可以是塑性应变的函数 (各向同性硬化/随动硬化). \(𝑟_𝑛\) 是应力状态和内变量的函数。
将(4)带入(5),可得:
\[\frac{\partial f}{\partial\sigma_{ij}}C_{ijkl}\left(d\varepsilon_{kl}-d\varepsilon_{kl}^p\right)+\frac{\partial f}{\partial q_n}\langle\lambda\rangle r_n=0
\]
将(2)带入(7),可得:
\[\frac{\partial f}{\partial\sigma_{ij}}C_{ijkl}d\varepsilon_{kl}-\frac{\partial f}{\partial\sigma_{ij}}C_{ijkl}\langle\lambda\rangle\frac{\partial Q}{\partial\sigma_{kl}}+\frac{\partial f}{\partial q_n}\langle\lambda\rangle r_n=0
\]
求得塑性应变增量:
\[\lambda
=\frac{\frac{\partial f}{\partial\sigma_{ij}}C_{ijkl}d\varepsilon_{kl}}{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}-\boxed{\frac{\partial f}{\partial q_{n}}r_{n}}}
=\frac{\frac{\partial f}{\partial\sigma_{ij}}C_{ijkl}d\varepsilon_{kl}}
{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}+\boxed{K_{p}}}
\]
三. 弹塑性刚度矩阵推导
将(9)带入(4),并化简,得到应力增量与应变增量的关系:
\[\begin{aligned}
&d\sigma_{ij}=C_{ijkl}\left(d\varepsilon_{kl}-\langle\lambda\rangle\frac{\partial Q}{\partial\sigma_{kl}}\right) \\
&C_{ijkl}\lambda\frac{\partial Q}{\partial\sigma_{kl}}=C_{ijmm}\frac{\partial Q}{\partial\sigma_{nm}}\frac{\frac{\partial f}{\partial\sigma_{pq}}C_{pqkl}d\varepsilon_{kl}}{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}-\frac{\partial f}{\partial q_{n}}r_{n}}=\frac{\left(C_{ijmm}\frac{\partial Q}{\partial\sigma_{nm}}\right)\left(\frac{\partial f}{\partial\sigma_{pq}}C_{pqkl}\right)d\varepsilon_{kl}}{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}+K_{p}} \\
&d\sigma_{ij}=C_{ijkl}\Bigg(d\varepsilon_{kl}-\langle\lambda\rangle\frac{\partial Q}{\partial\sigma_{kl}}\Bigg) \\
&=C_{ijkl}d\varepsilon_{kl}-\frac{\left(C_{ijmn}\frac{\partial Q}{\partial\sigma_{nm}}\right)\left(\frac{\partial f}{\partial\sigma_{pq}}C_{pqkl}\right)}{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}+K_{p}}d\varepsilon_{kl} \\
&=\left\{C_{ijkl}-\frac{\left(C_{ijmm}\frac{\partial Q}{\partial\sigma_{nm}}\right)\left(\frac{\partial f}{\partial\sigma_{pq}}C_{pqkl}\right)}{\frac{\partial f}{\partial\sigma_{ab}}C_{abcd}\frac{\partial Q}{\partial\sigma_{cd}}+K_{p}}\right\}d\varepsilon_{kl}&
\end{aligned}
\]
四. 塑性模量理解
式(9)定义了塑性模量:
\[K_p=-\frac{\partial f}{\partial q_n}r_n
\]
事实上,塑性模量的定义可以从一致性条件出发,带入(6),移项,即:
\[\begin{aligned}
&df=\frac{\partial f}{\partial\sigma_{ij}}d\sigma_{ij}+\frac{\partial f}{\partial q_{n}}dq_{n}=\frac{\partial f}{\partial\sigma_{ij}}d\sigma_{ij}+\frac{\partial f}{\partial q_{n}} \lambda dr_{n}=0 \\
&\frac{\frac{\partial f}{\partial\sigma_{ij}}d\sigma_{ij}}{\lambda}+\frac{\partial f}{\partial q_{n}}dr_{n}=0 \\
&K_{p}=\frac{\frac{\partial f}{\partial\sigma_{ij}}d\sigma_{ij}}{\lambda}=-\frac{\partial f}{\partial q_{n}}dr_{n}
\end{aligned}
\]
因此\(K_p\)可以理解为总应力增量在法向上的投影除以塑性应变增量,如下图所示:
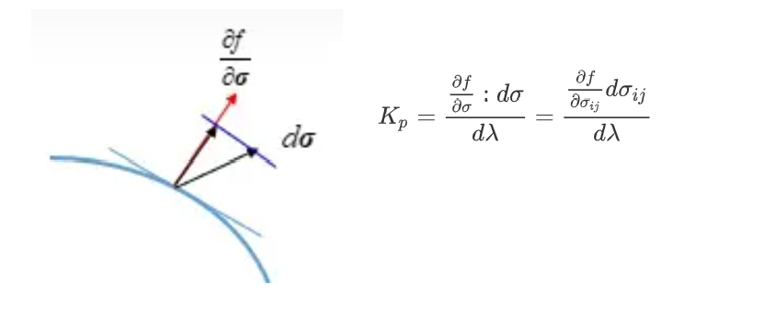
塑性模量是一个标量(方向沿屈服面法向),(注意尽管屈服面法向可能不是单位张量,总体上仍然可以反映塑性应变大小,只相差一个标量系数)
五. 小结
1)塑性力学核心三大概念;
2)通过一致性方程求解塑性应变增量,最终推导弹塑性刚度矩阵;
3)塑性模量的理解;
参考文献:
塑性力学本构模型基本框架 - 知乎 (zhihu.com)