2024.10.7 鲜花

news/2025/3/1 7:36:24/文章来源:https://www.cnblogs.com/xrlong/p/18450573

【UNR #3】百鸽笼

花の塔

君が持ってきた漫画
くれた知らない名前のお花
今日はまだ来ないかな？
初めての感情知ってしまった
窓に飾った絵画をなぞってひとりで宇宙を旅して
それだけでいいはずだったのに
君の手を握ってしまったら
孤独を知らないこの街には
もう二度と帰ってくることはできないのでしょう
君が手を差し伸べた　光で影が生まれる
歌って聞かせて　この話の続き
連れて行って見たことない星まで
誰の手も声も届かない
高く聳え立った塔の上へ
飛ばすフウセンカズラ
僕は君に笑って欲しいんだ
満たされない穴は惰性の会話や澄ましたポーズで
これまでは埋めてきたけど
退屈な日々を蹴散らして
君と二人でこの街中を泳げたら
それはどれだけ素敵なことでしょう？
出したことないほど大きな声でやっと君に伝わる
歪なくらいがさ　きっとちょうどいいね
世界の端と端を結んで
窓に飾った絵画をなぞってひとりで宇宙を旅して
それだけでも不自由ないけど
僕は選んでみたいの
高鳴る心　謎だらけの空を
安全なループを今、書き換えて！
君の手を握ってしまったら
孤独を知らないこの街にはもう二度と
帰ってくることはできないのでしょう
いくらでも迷いながら光も影も見に行こう
歌って聞かせてこの話の続き
連れて行って見たことない星まで
世界の端と端を結んで

愿天堂没有疾病和伤痛

好题。

首先转化，每次从还有剩余的笼中选实在抽象，考虑可以继续放进去，只是没有贡献。

于是将题面转化为：给定一个无限长的序列，其元素是每堆鸽笼编号，对于每个 \(i\in[1,n]\)，求对于所有 \(j\not=i\)，第 \(a_j\) 个 \(j\) 出现在第 \(a_i\) 个 \(i\) 之前的概率（其实是每个 \(i\) 从中选出前 \(a_i\) 个组成鸽笼）。

设当前处理的鸽笼编号为 \(i\)。

考虑容斥，枚举子集，设 \(f(S)\) 为恰好 \(S\) 的集合出现在 \(a_i\) 之后的概率，\(g(S)\) 为钦定（至少），有。

\[g(S)=\sum_{S\subseteq N} (-1)^{|N|-|S|} j(N) \]

\[ans=f(\varnothing)=\sum_{S} (-1)^{|S|} g(S) \]

考虑求 \(g(S)\)，设 \(dp_{i,j}\) 表示从 \(S\) 中选到前 \(i\) 个，一共长度为 \(j\) 的方案数，枚举第 \(i\) 个选 \(k\) 个，背包显然转移。

因为是有序的，记得在转移时乘上 \(\frac{1}{k!}\)，乘上 \(j!\)，还要记得乘上 \(a_i-1\) 的插板。

有了方案数，概率显然是 \(\sum\limits_i \frac{dp_{n,i}}{n^i}\)。

这样已经有了 \(30pts\) 做法。

考虑去掉指数，考虑转移过程，发现其只和 \(|S|\) 有关，考虑多加一位 \(dp_{l,i,j}\) 表示一共选了 \(l\) 堆笼子，枚举第 \(l\) 个是否选和选了多少来转移（相当于是把 \(|S|\) 相同的一起转移），依然是类似背包转移。

这里已经是 \(n^6\) 的做法了，但是不好过，考虑经典 trick 可退回背包，可以做到 \(n^5\)。

Code

#include<bits/stdc++.h>
using namespace std;
using llt=long long;
using llf=long double;
using ull=unsigned long long;
#define endl '\n'
#ifdef LOCALFILE *InFile=freopen("in_out/in.in","r",stdin),*OutFile=freopen("in_out/out.out","w",stdout);
#elseFILE *InFile=stdin,*OutFile=stdout;
#endifconst int N=33,MOD=998244353;
int c[N],n,m,fac[N*N],ivf[N*N],dp[N][N*N];int Fpw(int a,int b){int ans=1;while(b){if(b&1) ans=1ll*ans*a%MOD;a=1ll*a*a%MOD,b>>=1;}return ans;
}
int Inv(int a){return Fpw(a,MOD-2);}
int C(int a,int b){return 1ll*fac[a]*ivf[b]%MOD*ivf[a-b]%MOD;}void Del(int i){for(int l=1;l<=n;++l) for(int j=0;j<=m;++j) for(int k=0;k<=min(j,c[i]-1);++k)dp[l][j]=(dp[l][j]-1ll*dp[l-1][j-k]*ivf[k]%MOD+MOD)%MOD;
}
void Add(int i){for(int l=n;l;--l) for(int j=m;j>=0;--j) for(int k=0;k<=min(j,c[i]-1);++k)dp[l][j]=(dp[l][j]+1ll*dp[l-1][j-k]*ivf[k])%MOD;
}
int main(){ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);cin>>n; for(int i=1;i<=n;++i) cin>>c[i],m+=c[i];fac[0]=1; for(int i=1;i<=m;++i) fac[i]=1ll*fac[i-1]*i%MOD;ivf[m]=Inv(fac[m]); for(int i=m;i;--i) ivf[i-1]=1ll*ivf[i]*i%MOD;dp[0][0]=1; for(int i=1;i<=n;++i) Add(i);for(int nw=1;nw<=n;++nw){Del(nw); int ans=0;for(int j=0;j<n;++j){int tmp=0;for(int k=0;k<=m-c[nw];++k) tmp=(tmp+1ll*dp[j][k]*fac[k]%MOD*C(c[nw]+k-1,k)%MOD*Inv(Fpw(j+1,k+c[nw]))%MOD)%MOD;ans=((ans+tmp*((j&1)?-1:1))%MOD+MOD)%MOD;}cout<<ans<<' ';Add(nw);}
}

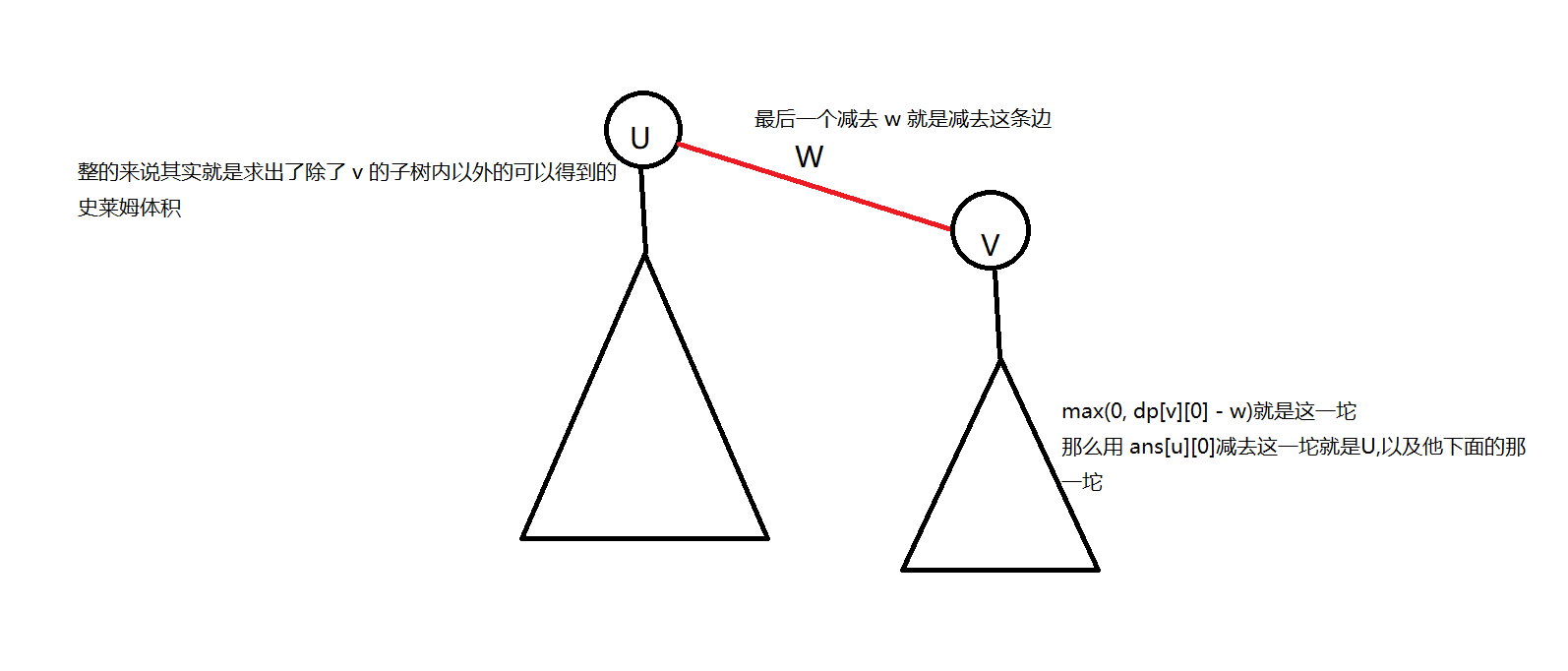
图，话说为什么这么多人喜欢用多个折叠，这个东西可以直接 F12 一键展开的 QwQ