渥太华大学的研究人员与罗马大学的Danilo Zia和Fabio Sciarrino合作,展示了一种新技术,可以实时可视化两个纠缠光子(构成光的基本粒子)的波函数。

研究成果以“Interferometric imaging of amplitude and phase of spatial biphoton states”为题,发表在《自然·光子学》(Nature Photonics)上。
用一双鞋作比喻,纠缠的概念可以比作随机选择一只鞋。当你辨认出一只鞋子的那一刻,另一只鞋子的性质(是左鞋还是右鞋)就会立刻被分辨出来,而不管它在宇宙中的位置如何。然而,耐人寻味的是,在观察的确切时刻之前,与识别过程相关的固有不确定性。
波函数是量子力学的核心原理,它提供了对粒子量子态的全面理解。例如,在鞋子的例子中,鞋子的“波函数”可以携带左右、大小、颜色等信息。
更准确地说,波函数使量子科学家能够预测对量子实体进行各种测量的可能结果,如位置、速度等。
这种预测能力非常宝贵,尤其是在飞速发展的量子技术领域,了解量子计算机产生或输入的量子态,就可以测试计算机本身。此外,量子计算中使用的量子态极其复杂,涉及许多可能表现出强非局域性(纠缠)的实体。
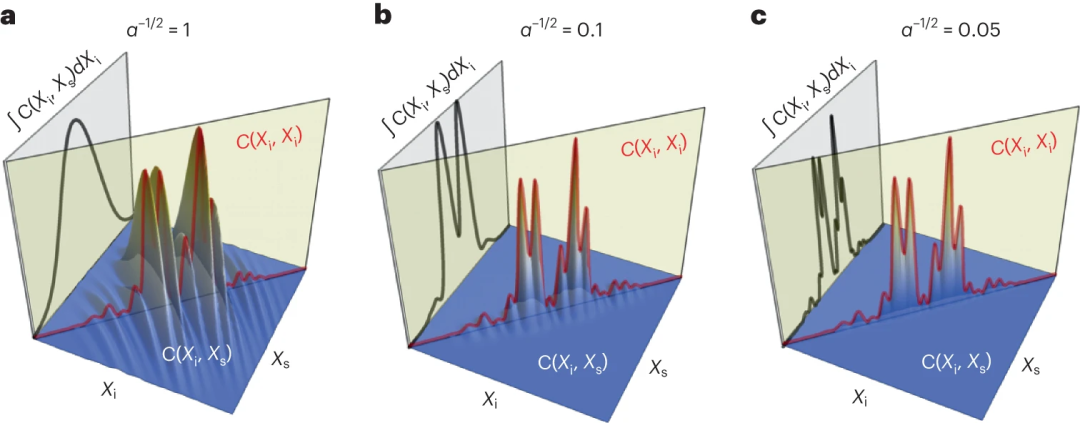
了解这样一个量子系统的波函数是一项极具挑战性的任务——这也被称为量子态层析或简称量子层析。采用标准方法(基于所谓的射影变换projective operations)进行全面层析需要大量测量,而测量次数会随着系统复杂度(维度)的增加而迅速增加。
此次,这个研究小组以前用这种方法进行的实验表明,表征或测量两个纠缠光子的高维量子态可能需要几个小时甚至几天的时间。并且,结果的质量对噪声非常敏感,这些结果的质量还取决于实验装置的复杂程度。
量子层析成像的射影测量方法可以理解为观察从独立方向投射到不同墙壁上的高维物体的影子。研究人员所能看到的就是这些阴影,而从这些阴影中,他们可以推断出整个物体的形状(状态)。例如,在 CT 扫描(计算机断层扫描)中,可以从一组二维图像中重建三维物体的信息。
不过,在经典光学中,还有另一种重建三维物体的方法。这种方法被称为数字全息术(digital holography),其基础是记录单幅图像——即干涉图(interferogram),通过将物体散射的光与参考光进行干涉而获得。
由加拿大结构量子波研究主席、渥太华量子技术联合研究所(NexQT)联合主任、理学院副教授Ebrahim Karimi领导的研究小组将这一概念扩展到了双光子的情况。
重构双光子态需要将其与假定的、众所周知的量子态叠加,然后分析两个光子同时到达的位置的空间分布。对同时到达的两个光子进行成像被称为幽灵成像(coincidence image)。这些光子可能来自参考源,也可能来自未知源。量子力学指出,光子的来源无法确定。
这就产生了一种干涉模式,可用于重建未知波函数。先进的照相机能以纳秒级的分辨率记录每个像素上的事件,使这项实验成为可能。
双光子态全息重建
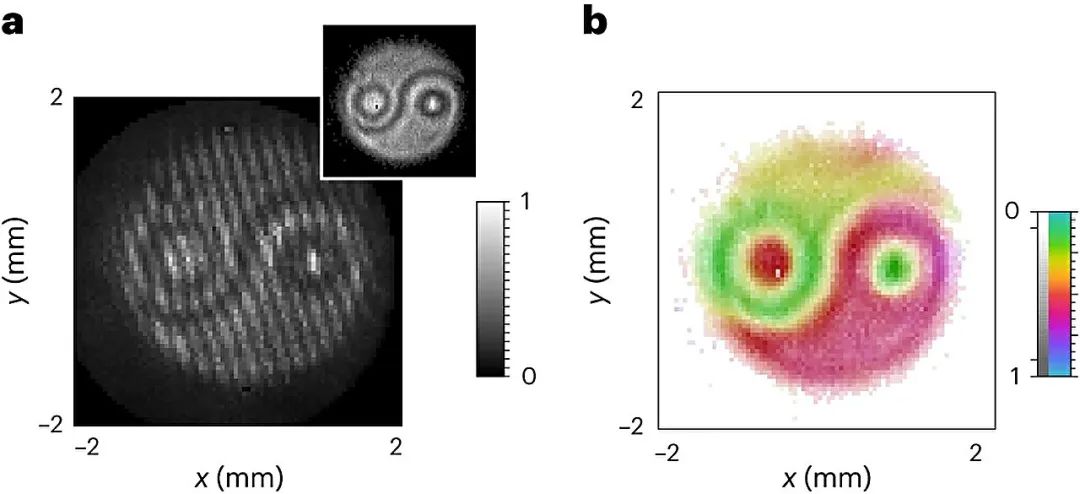
图像重建。a)参考 SPDC 状态与由泵浦光束获得的状态之间的干涉重合图像,其形状为阴阳符号(如插图所示)。插图中的比例与主图中的比例相同。b)在未知泵浦上印刻的图像的重建振幅和相位结构。
论文共同作者之一、渥太华大学博士后 Alessio D'Errico 博士强调了这种创新方法的巨大优势:“这种方法比以前的技术快了数倍,只需要几分钟或几秒钟,而不是几天。重要的是,检测时间不受系统复杂性的影响——这就解决了投影断层成像中长期存在的可扩展性难题。”
这项研究的影响不仅限于学术界。它有可能加速量子技术的进步,如改进量子态表征、量子通信和开发新的量子成像技术。
参考链接:
[1]https://phys.org/news/2023-08-visualizing-mysterious-quantum-entanglement-photons.html
[2]https://www.nature.com/articles/s41566-023-01272-3