GaussDB Kernel V5版本的Catalog还是本地存储, 所以还需要考虑catalog的持久化问题.未来演进元数据解耦,Coordinator 无状态, 就不需要考虑Catalog持久化问题了。但是跨节点场景下的事务提交在Coordinator上还是要持久化的。

图14 Coordinator模块图
路由信息:每个表数据共分16384个hash bucket来存储,每个DN对应存储若干个hash bucket的数据。SQL优化器模块会根据Query的条件自动剪枝DN。
Pooler连接池:维护和每个DN连接的socket信息,缓存建立的连接。
3.1 分布式优化器
优化器的查询重写基础依赖于关系代数的等价变换。等价变换关系如下图所示:

图15 关系代数的等价变换
基于规则的查询重写,基本规则如下。
常量化简:如 SELECT * FROM t1 WHERE c1=1+1; 等价于SELECT * FROM t1 WHERE c1=2;
消除DISTINCT:CREATE TABLE t1(c1 INT PRIMARY KEY, c2 INT); SELECT DISTINCT(c1) FROM t1; SELECT c1 FROM t1;
IN谓词展开:SELECT * FROM t1 WHERE c1 IN (10,20,30); 等价于SELECT * FROM t1 WHERE c1=10 or c1=20 OR c1=30;
视图展开:CREATE VIEW v1 AS (SELECT * FROM t1,t2 WHERE t1.c1=t2.c2); SELECT * FROM v1; 等价于 SELECT * FROM t1,t2 WHERE t1.c1=t2.c2;
条件下移:t1 join t2 on … and t1.b=5 等价于 (t1 where t1.b=5) join t2
条件传递闭包:a=b and a=3 -> b=3
消除子链接:如 select * from t1 where exists(select 1 from t2 where t1.a=t2.a); 等级于 select * from t1 (semi join) (select a from t2) t2 where t1.a=t2.a;
…
查询重写规则较多,在此不一一列举。
在基于代价的查询优化技术上,主要关注三个关键问题。分别是:结果集行数估算、执行代价估算以及路径搜索。其核心目标是,为多个物理执行的代价进行评分,最后选择出一个最优的计划,输出到执行器。
行数估算方面,通过analyze手段,收集基表的统计信息,统计信息包括:各个数据表的规模、行数以及页面数等。在表中,也会统计各个列的信息,包括distinct值(该列不相同的值的个数),空值的比例,MCV(most common value,用于记录数据倾斜情况)以及直方图(用于记录数据分布情况),根据基表统计信息,估算过滤、join的中间结果统计信息。未来将基于AI进行多维度统计信息收集,收集更准确的行数信息,以辅助更优的计划选择。
执行代价估算方面,根据数据量估算不同算子的执行代价,各个执行算子的代价之和即为执行计划的总代价。算子的代价,主要包含几个方面:CPU代价、IO代价、网络代价(分布式多分片场景)等。未来需要根据物理环境的不同,调整不同算子的执行代价比例,同时通过AI技术构建更精准的代价模型。
表1 代价估算算子种类

路径搜索方面,GaussDB Kernel V5采用自底向上的路径搜索算法,对于单表访问路径,一般有两种:
全表扫描:对表中的数据逐个访问。
索引扫描:借助索引来访问表中的数据,通常需要结合谓词一起使用。
优化器首先根据表的数据量、过滤条件、和可用的索引结合代价模型来估算各种不同扫描路径的代价。例如:给定表定义CREATE TABLE t1(c1 int); 如果表中数据为1,2,3…100000000连续的整型值并且在c1列上有B+树索引,那么对于SELECT * FROM t1 WHERE c1=1; 来说,只要读取1个索引页面和1个表页面就可以获取到数据。然而对于全表扫描,需要读取1亿条数据才能获取同样的结果。在这种情况下索引扫描的路径胜出。
索引扫描并不是在所有情况下都优于全表扫描,它们的优劣取决于过滤条件能够过滤掉多少数据,通常数据库管理系统会采用B+树来建立索引,如果在选择率比较高的情况下,B+树索引会带来大量的随机I/O,这会降低索引扫描算子的访问效率。比如SELECT * FROM t1 WHERE c1>0;这条语句,索引扫描需要访问索引中的全部数据和表中的全部数据,并且带来巨量的随机I/O,而全表扫描只需要顺序的访问表中的全部数据,因此在这种情况下,全表扫描的代价更低。
多表路径生成的难点主要在于如何枚举所有的表连接顺序(Join Reorder)和连接算法(Join Algorithm)。假设有两个表t1和t2做JOIN操作,根据关系代数中的交换律原则,可以枚举的连接顺序有t1 × t2和t2 × t1两种,JOIN的物理连接算子有Hash Join、Nested Loop Join、Merge Join三种类型。这样一来,可供选择的路径有6种之多。这个数量随着表的增多会呈指数级增长,因此高效的搜索算法显得至关重要。GaussDB Kernel 通常采用自底向上的路径搜索方法,首先生成了每个表的扫描路径,这些扫描路径在执行计划的最底层(第一层),在第二层开始考虑两表连接的最优路径,即枚举计算出每两表连接的可能性,在第三层考虑三表连接的最优路径,即枚举计算出三表连接的可能性,直到最顶层为止生成全局最优的执行计划。假设有4个表做JOIN操作,它们的连接路径生成过程如下:
单表最优路径:依次生成{1},{2},{3},{4}单表的最优路径。
二表最优路径:依次生成{1 2},{1 3},{1 4},{2 3},{2 4},{3 4}的最优路径。
三表最优路径:依次生成{1 2 3},{1 2 4},{2 3 4},{1 3 4}的最优路径。
四表最优路径:生成{1 2 3 4}的最优路径即为最终路径。
多表路径问题核心为Join Order,这是NP(Nondeterministic Polynomially,非确定性多项式)类问题,在多个关系连接中找出最优路径,比较常用的算法是基于代价的动态规划算法,随着关联表个数的增多,会发生表搜索空间膨胀的问题,进而影响优化器路径选择的效率,可以采用基于代价的遗传算法等随机搜索算法来解决。
另外为了防止搜索空间过大,可以采用下列三种剪枝策略:
尽可能先考虑有连接条件的路径,尽量推迟笛卡尔积。
在搜索的过程中基于代价估算对执行路径采用LowBound剪枝,放弃一些代价较高的执行路径。
保留具有特殊物理属性的执行路径,例如有些执行路径的结果具有有序性的特点,这些执行路径可能在后序的优化过程中避免再次排序。
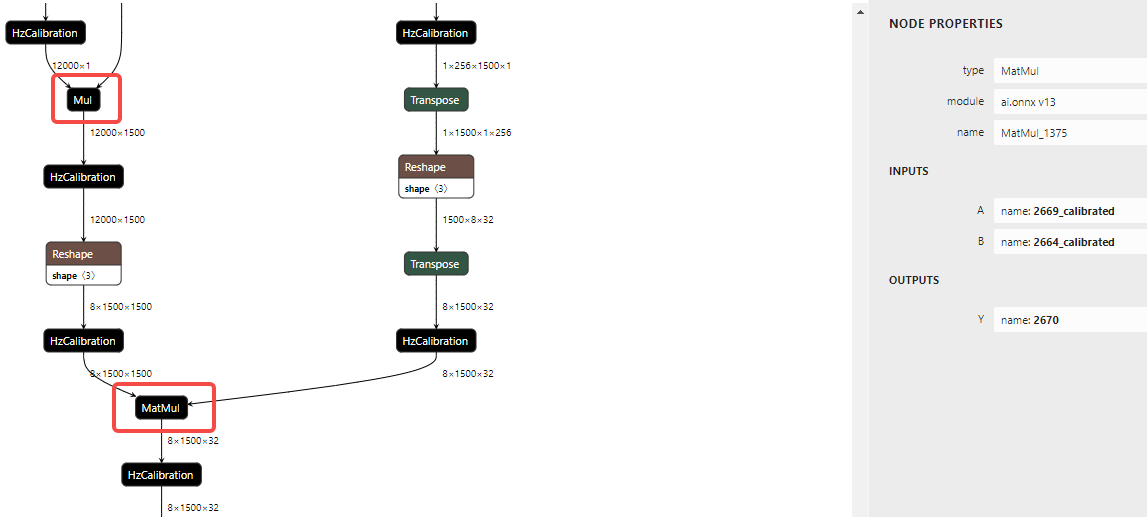
分布式执行计划生成方面,相关关键技术流程如图所示:

图16 分布式执行计划生成