二维前缀和模板
题目描述:
输入一个 n 行 m 列的整数矩阵,再输入 q个询问,每个询问包含四个整数 x1,y1,x2,y2,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式:
第一行包含三个整数 n,m,q
接下来 n 行,每行包含 m 个整数,表示整数矩阵。
接下来 q行,每行包含四个整数 x1,y1,x2,y2,表示一组询问。
输出格式:
共 q行,每行输出一个询问的结果。
数据范围:
1≤n,m≤1000
1≤q≤200000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
解题思路:
我们首先要理解,sum[i,j]是什么意思。
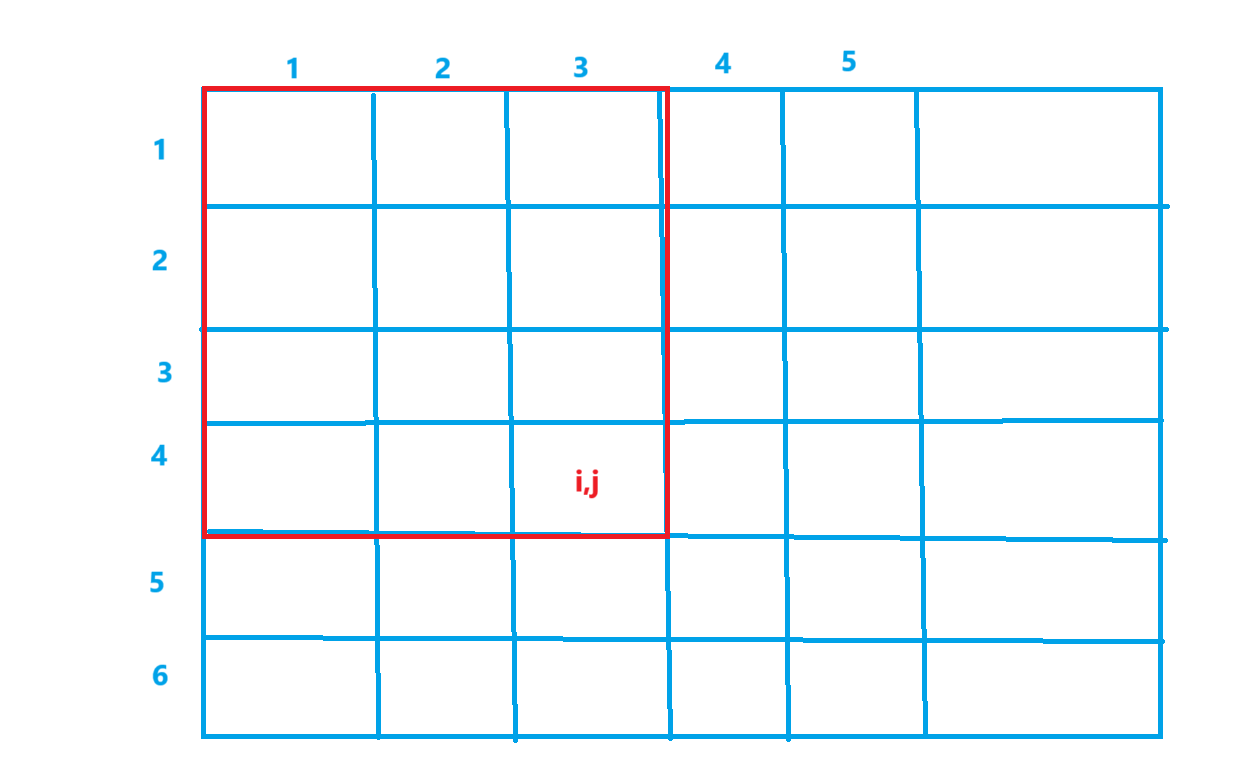
如图所示,sum[i,j]就是红色区域所包含的所有数之和.
但是题目要求我们把,[x1,y1]到[x2,y2]区域内数之和求出来,所以我们可以再画一个图.
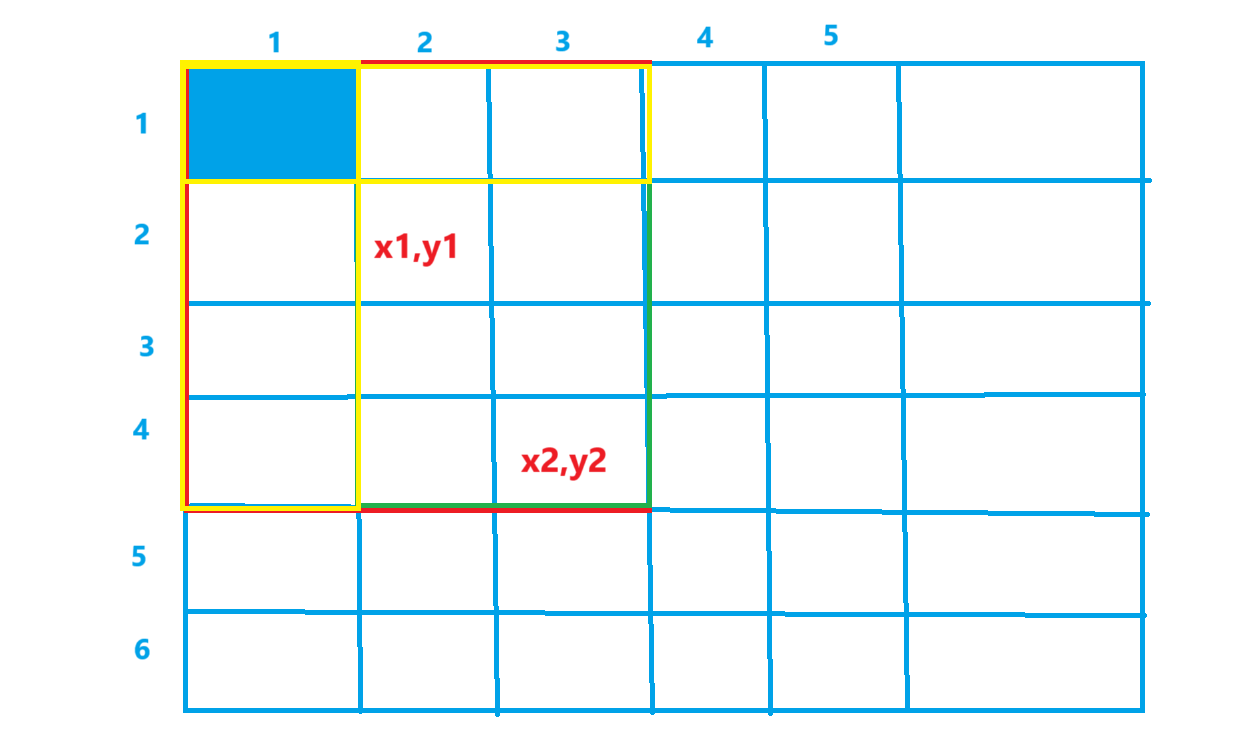
如图所示,我们要求[x1,y1]到[x2,y2]内所有数之和,是不是可以让sum[x2,y2]减去黄色区域之和,也就是sum[x2,y2]-sum[x1-1,y2]-sum[x2,y1-1],但是我们会发现,这样会使蓝色区域被减两边,所以我们还需要把蓝色区域加一遍,最终表达式也就是
sum[x2,y2]-sum[x1-1,y2]-sum[x2,y1-1]+sum[x1-1,y1-1]
还有一步,我们要处理这个前缀和。
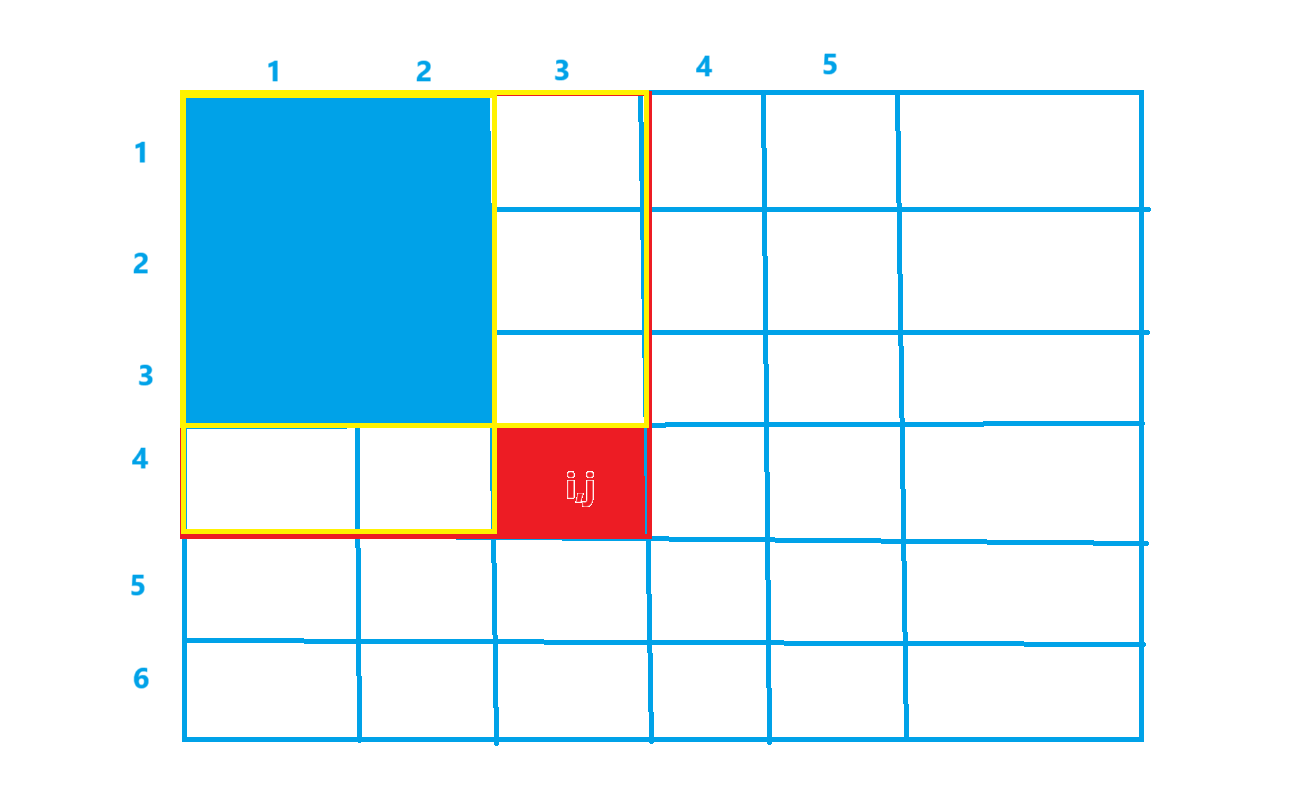
如图,我们要求sum[i,j],先让黄色区域加起来,也就是sum[i-1,j]+sum[i,j-1],这样会让蓝色区域加重,再减去蓝色区域,也就是sum[i-1,j-1],最后再加上a[i,j]就是我们要求的式子。
表达式如下:
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int n,m,q;
int a[N][N],sum[N][N];
int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);}}//处理前缀和 for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];}}//询问 while(q--){int x1,y1,x2,y2;scanf("%d%d%d%d",&x1,&y1,&x2,&y2);printf("%d\n",sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]);}return 0;
}