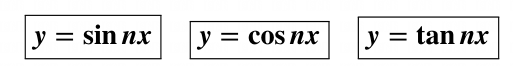2 三角函数 II
学完本章内容后,你应该能够
● 讨论反三角函数的图形
● 讨论倒数函数的图形
● 评估正弦、余弦和正切函数的变换
2.1 引言
本章将继续讨论三角函数,研究上一章中涉及的三个三角函数的倒数和反三角函数。本章还将讨论这些函数的变换。
2.2 三角函数的倒数
正弦、余弦和正切的倒数分别称为余割、正割和余切;简称为 cosec、sec 和 cot。请注意,每个名称的第三个字母表示我们所指的倒数。根据三个字母的惯例,cosec 进一步缩写为 csc。
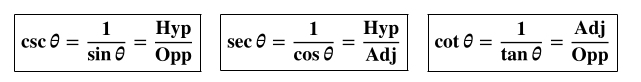
2.2.1 余弦&余割
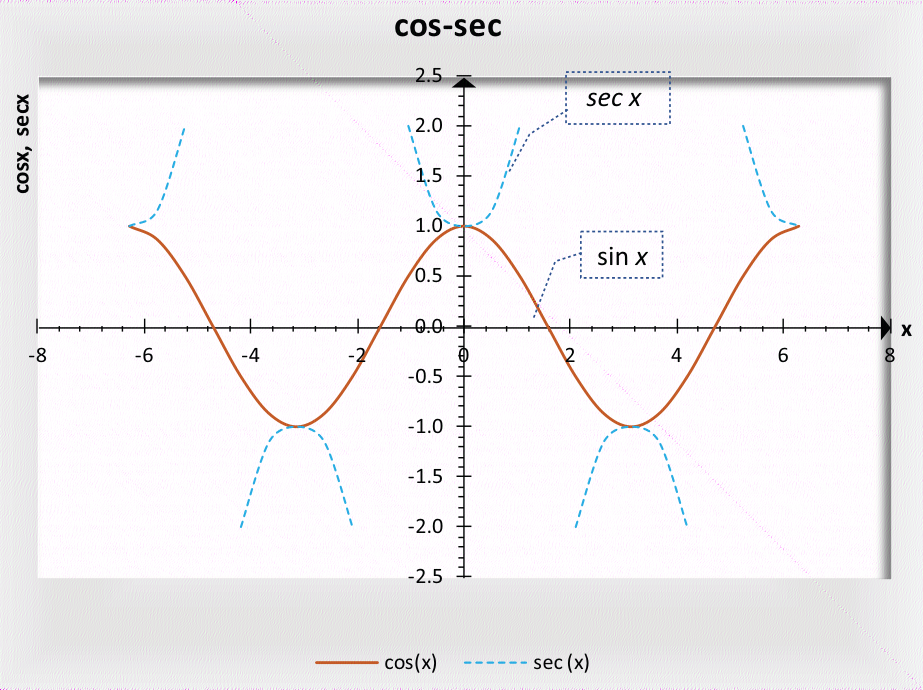
2.2.2 正弦&正割
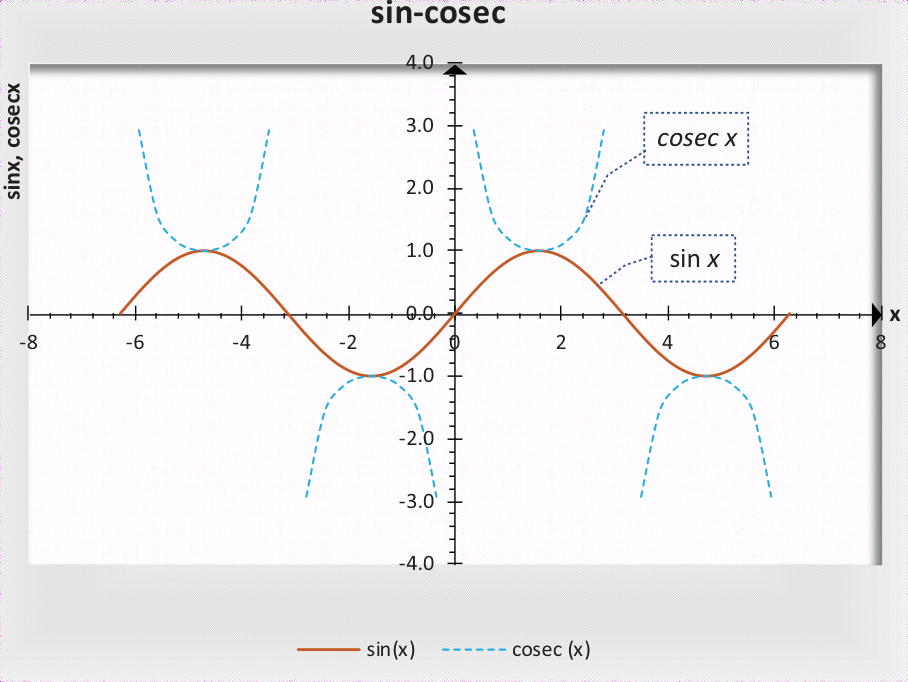
2.2.3 正切&余切
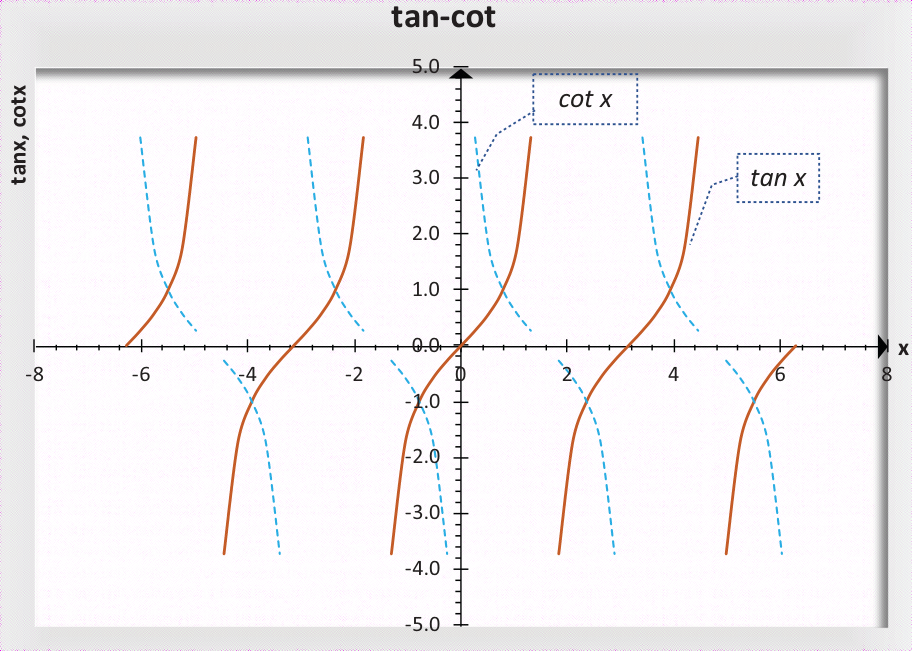
2.3 反三角函数
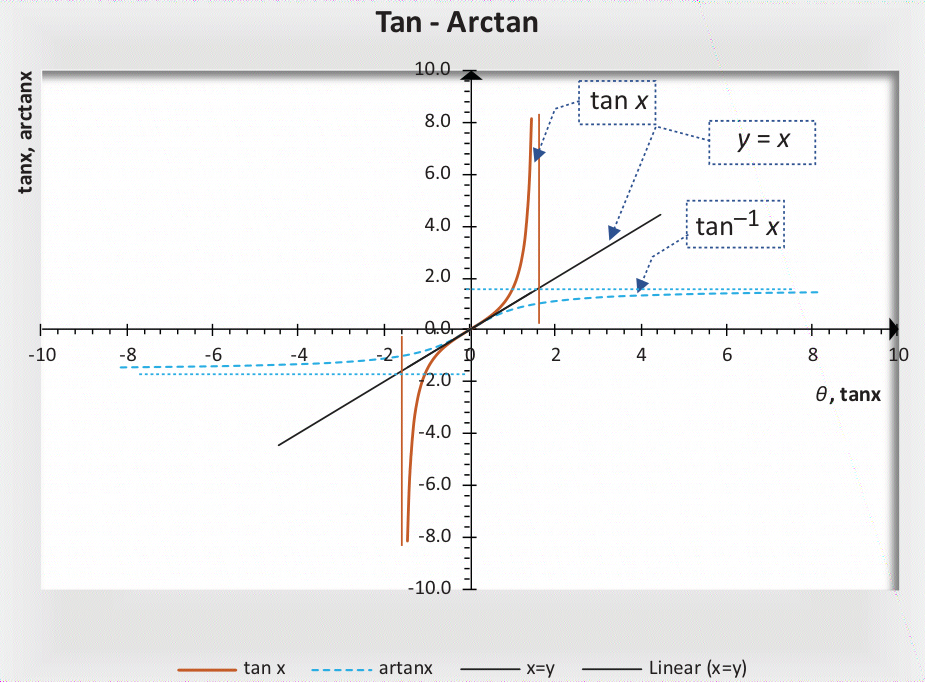
在第 1 章中,我们讨论了反三角函数。这里将再次讲解,但重点是它们的图形。一般来说,三角函数是多对一的函数;也就是说,自变量 x 的一个以上的值会得到因变量(sin x、cos x 或 tan x)的相同值。例如,sin 0 = sin 𝜋 = sin 2𝜋 = 0,cos 0 = cos 𝜋 = cos (-𝜋) = -1,tan 0 = tan 𝜋 = tan (-𝜋) = 0。
因此,要绘制反函数图,我们需要限制域,使三角比的表现如同它是一个一一对应的函数。一旦我们开始研究每个函数,这一点就会更加清楚。所有三角函数反函数的一个共同特征是,它们都是各自函数沿 y = x 轴的镜像。
2.3.1 ARCSIN函数
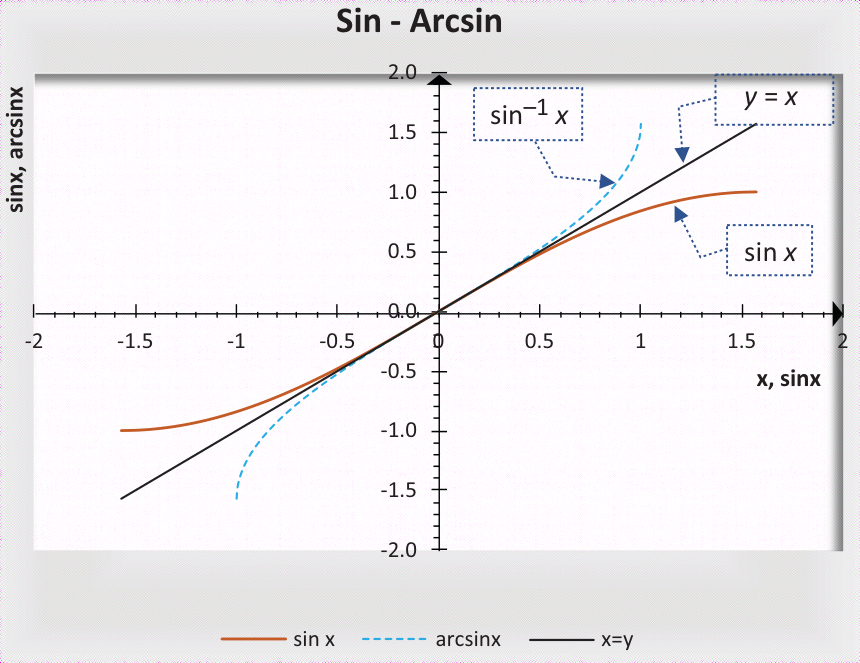
2.3.2 ARCCOS函数
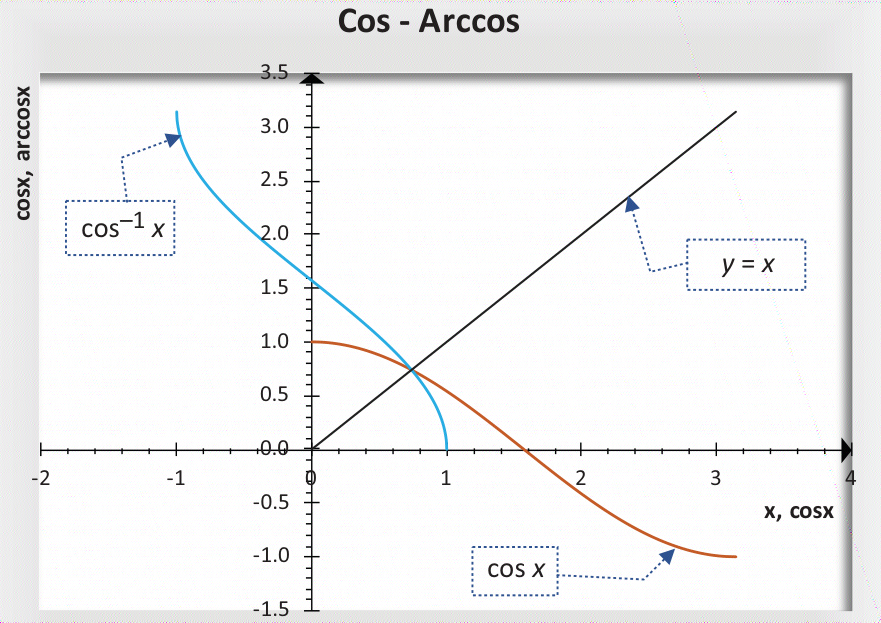
2.3.3 ARCTAN函数
2.4 三角函数变换
变换是指图形函数形状的改变,可以通过几种方式实现。在此,我们将研究三角函数的两大类变化,即平移和拉伸。
2.4.1 平移
这是正弦、余弦和正切图形沿 x-y 平面的移动(不改变形状),主要有两种类型。
- 水平平移
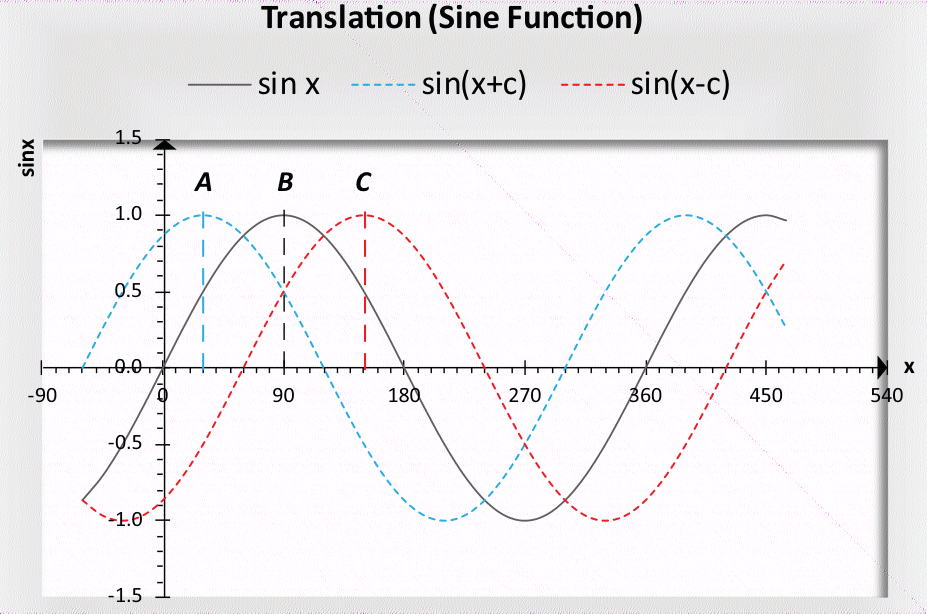
是指图形沿 x 轴左右移动。给定正弦函数 f (x) = sin x,该函数的平移值为 g (x) = sin (x ± c),其中 c 为正数(即 c > 0),表示移动的角度。
g1 (x) = sin (x + c) 是一个向 f (x) 左边移动的图形,可以说它以 c 的角度领先于 sin x;同样,g2 (x) = sin (x - c) 是一个向 f (x) 右边移动的图形,可以说它以 c 的角度落后于 sin x。
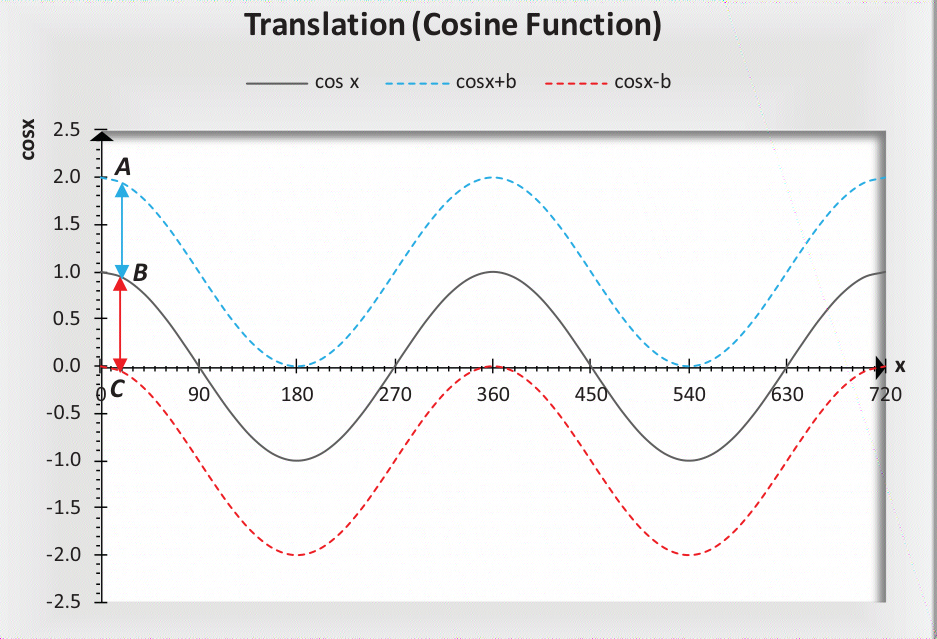
- 垂直平移
是指图形沿 y 轴向上或向下移动。给定余弦函数 f (x) = cos x,该函数的平移公式为 g (x) = cos x ± b,其中 b 为正数(即 b > 0),表示平移的长度。
2.4.2 伸展(拉伸 STRETCH)
这是三角函数沿 x 轴或 y 轴进行 “变换 ”的过程。这种变换会导致形状的放大和缩小。
- 垂直拉伸
这是指图形在 y 轴方向上被拉伸或压扁。这种类型的一般形式如下所示,适用于三个三角函数。
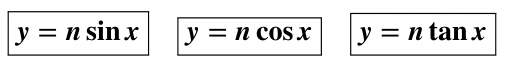

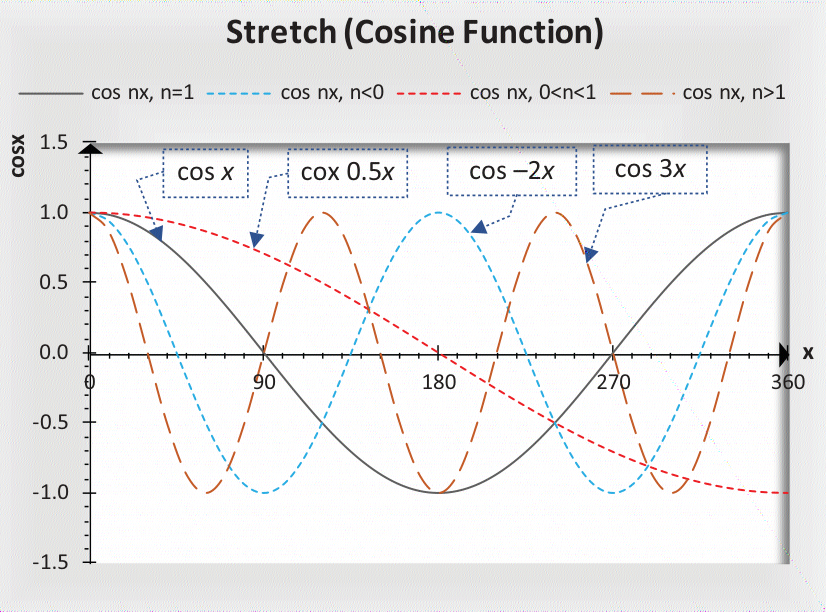
- 水平拉伸
是指图形在 X 轴方向上被拉伸(或缩小)。其一般形式为