[!TIP]
一种剪枝算法,优化运算效率,减少冗余计算
基本内容
- 入门例子 [P1028 [NOIP2001 普及组] 数的计算]([P1028 NOIP2001 普及组] 数的计算 - 洛谷 | 计算机科学教育新生态)
题目要求:输入n,输出一共可以构造多少个数列,要求数列的第
i不能超过第i-1个数的一半示例:输入6,只能输出 [6], [6, 1], [6, 2], [6, 3], [6, 2, 1], [6, 3, 1] 一共六种
- 传统思路,深度优先搜索算法,可以发现大部分案例都 TLE(超时)了
n = int(input())
ans = 0
def f(x):global ansans += 1for i in range(1, int(x/2)+1):f(i)f(n)
print(ans)
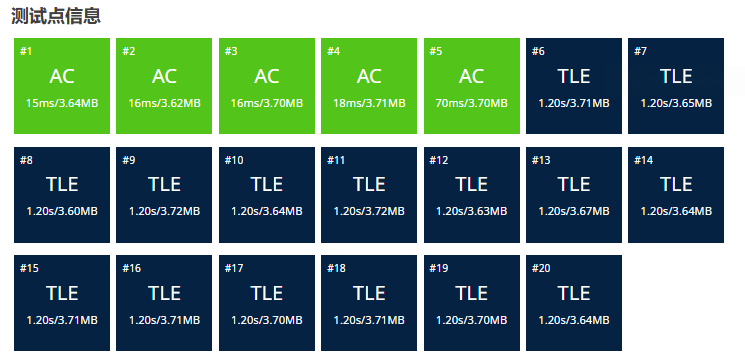
- 超时分析:存在着重复计算的数列
重复子问题,以输入8为例,当我们计算出[8, 2, 1]时就知道了当输入为2时只有俩个可以满足的序列,以此类推,当我们以32为输入,计算到[36, 16, 8 ....] 得知子树8共有 10 种数列时,即可直接计算 [36, 8] 共有11种满足的数列。
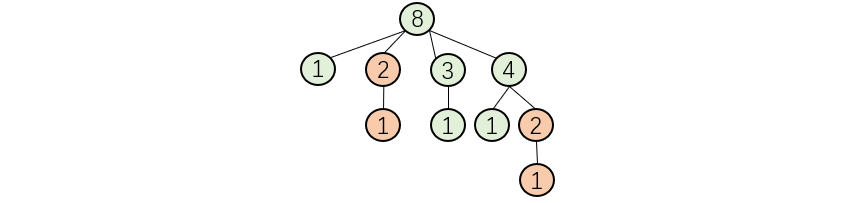
- 记忆化搜索:额外开辟一个数组空间
cache存储计算过的值
n = int(input())
cache = [-1] * (n+1)
def f(x):if cache[x] != -1: # cache 不为-1表示已经计算过return cache[x]ans = 1 # 每一个数字都可以表示单独为一个数列for i in range(1, int(x/2)+1):ans += f(i)cache[x] = ansreturn ansprint(f(n))
题目
- Leetcode 638. 大礼包
本来想用贪心算法去做,行不通,还是需要遍历每一种情况
class Solution:def shoppingOffers(self, price: List[int], special: List[List[int]], needs: List[int]) -> int:cache = {}def dfs(needs: Tuple[int]) -> int:if needs in cache: # 若need被计算过则返回need所需的最小花费return cache[needs]min_cost = 0 # 不用礼包的低消for i in range(len(price)):min_cost += (needs[i] * price[i])for offer in special: # 因为礼包可以无限次使用,每次都需要遍历每一个礼包new_needs = []for i in range(len(needs)):if needs[i] < offer[i]: # 如果大礼包的物品超出需求,跳过breaknew_needs.append(needs[i] - offer[i])else: # 表示for循环没有被break,计算当前使用该礼包是否可以得到最小值min_cost = min(min_cost, dfs(tuple(new_needs)) + offer[-1])cache[needs] = min_costreturn min_costreturn dfs(tuple(needs))